
题目列表(包括答案和解析)
5. (2011四川南充市,9,3分)在圆柱形油槽内装有一些油。截面如图,油面宽AB为6分米,如果再注入一些油 后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
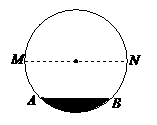
(A)6分米 (B)8分米 (C)10分米 (D)12分米
[答案]C
4. (2011山东泰安,10 ,3分)如图,⊙O的弦AB垂直平分半径OC,若AB=,则⊙O的半径为( )
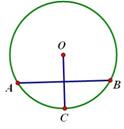
A. B.2 C. D.
[答案]A
3.
(2011福建福州,9,4分)如图2,以 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦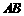 切小圆于点
切小圆于点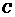 ,若
,若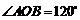 ,则大圆半径
,则大圆半径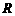 与小圆半径
与小圆半径 之间满足( )
之间满足( )
A.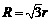 B.
B.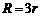 C.
C.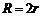 D.
D.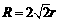
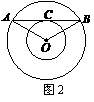
[答案]C
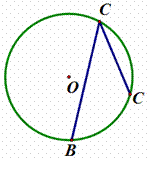
2. (2011安徽,7,4分)如图,⊙O的半径是1,A、B、C是圆周上的三点,∠BAC=36°,则劣弧的长是( )
A. B.π C.π D.π
[答案]B
1. (2011广东湛江16,4分)如图,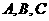 是
是 上的三点,
上的三点,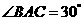 ,则
,则 度.
度.

[答案]60
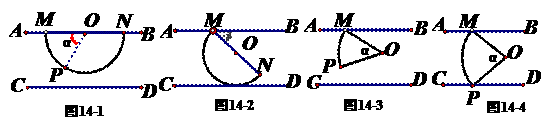
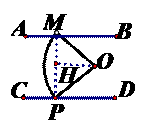
27. (2011河北,25,10分)如图14-1至14-4中,两平行线AB,CD间的距离为6,点M为AB上一定点.
思考
如图14-1,圆心为O的半圆纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α.
当α= 度时,点P到CD的距离最小,最小值为 。
探究一
在图14-1的基础上,以点M为旋转中心,在AB,CD之间顺时针旋转该半圆纸片,直到不能再转动为止,如图14-2,得到最大旋转角∠BMO= 度,此时点N到CD的距离是
探究二
将图14-1中的扇形纸片NOP按下面对α要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转。
(1)如图14-3,当α=60°时,球在旋转过程中,点p到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图14-4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的取值范围.
(参考数据:sin49°=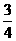 ,cos41°=
,cos41°=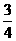 ,tan37°=
,tan37°=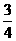 )
)
[答案]思考 90,2;
探究一 30,2;
探究二
(1)由已知得M与P的距离为4,∴当MP⊥AB时,点P到AB的最大距离为4,从而点P到CD的最小距离为6-4=2.当扇形MOP在AB,CD之间旋转到不能再转时,弧MP与AB相切,此时旋转角最大,∠BMO的最大值为90°。
(2)如图,由探究一可知,点P是弧MP与CD的切点时,α达到最大,即OP⊥CD。此时延长PO交AB于点H,α最大值为∠OMH+∠OHM=30°+90°=120°。
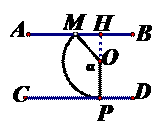
如图,当点P在CD上且与AB距离最小时,MP⊥CD,α达到最小,连接MP,作OH⊥MP于点H,由垂径定理,得MH=3,在Rt△MOH中,MO=4,∴sin∠MOH=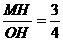 ,∴∠MOH=49°,∵α=2∠MOH,∴α最小值为98°。∴α的取值范围是98°≤α≤120°。
,∴∠MOH=49°,∵α=2∠MOH,∴α最小值为98°。∴α的取值范围是98°≤α≤120°。
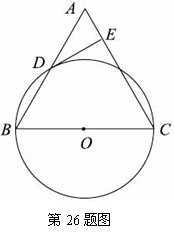
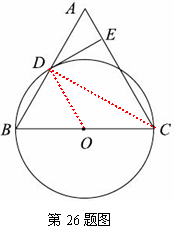
26. (2011贵州安顺,26,12分)已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
⑴求证:点D是AB的中点;
⑵判断DE与⊙O的位置关系,并证明你的结论;
⑶若⊙O的直径为18,cosB =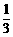 ,求DE的长.
,求DE的长.

[答案](1)证明:连接CD,则CD , 又∵AC = BC,
CD = CD, ∴
, 又∵AC = BC,
CD = CD, ∴ ≌
≌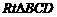
∴AD = BD , 即点D是AB的中点.

(2)DE是⊙O的切线 .
理由是:连接OD, 则DO是△ABC的中位线,∴DO∥AC , 又∵DE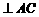 ;
;
∴DE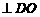 即DE是⊙O的切线;
即DE是⊙O的切线;
(3)∵AC = BC, ∴∠B =∠A , ∴cos∠B = cos∠A =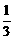 , ∵ cos∠B
=
, ∵ cos∠B
=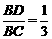 ,
BC = 18,
,
BC = 18,
∴BD = 6 , ∴AD = 6 ,
∵ cos∠A =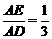 , ∴AE = 2,
, ∴AE = 2,
在 中,DE=
中,DE=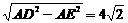 .
.
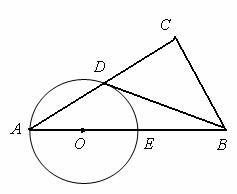
25. (2011广东湛江27,12分)如图,在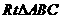 中,
中,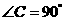 ,点D是AC的中点,且
,点D是AC的中点,且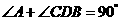 ,过点
,过点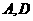 作
作 ,使圆心
,使圆心 在
在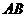 上,
上, 与
与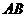 交于点
交于点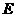 .
.
(1)求证:直线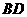 与
与 相切;
相切;
(2)若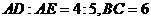 ,求
,求 的直径.
的直径.
[答案](1)证明:连接OD,在 中,OA=OD,
中,OA=OD,
所以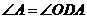 ,
,
又因为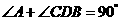 ,
,
所以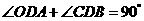 ,所以
,所以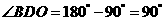 ,即
,即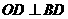 ,
,
所以BD与 相切;
相切;
(2)由于AE为直径,所以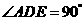 ,由题意可知
,由题意可知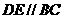 ,又点D是AC的中点,且
,又点D是AC的中点,且
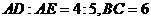 ,所以可得
,所以可得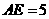 ,即
,即 的直径为5.
的直径为5.
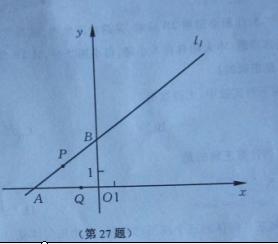
24. (20011江苏镇江27,9分)在平面直角坐标系xOy中,一次函数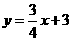 的图象是直线
的图象是直线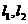 与x轴、y轴分别相交于A、B两点.直线
与x轴、y轴分别相交于A、B两点.直线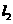 过点C(a,0)且与
过点C(a,0)且与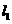 垂直,其中a>0,点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
垂直,其中a>0,点P、Q同时从A点出发,其中点P沿射线AB运动,速度为每秒4个单位;点Q沿射线AO运动,速度为每秒5个单位.
(1)写出A点的坐标和AB的长;
(2)当点P、Q运动了t秒时,以点Q为圆心,PQ为半径的⊙Q与直线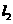 、y轴都相切,求此时a的值.
、y轴都相切,求此时a的值.
答案:(1)A(-4,0),AB=5.
(2)由题意得:AP=4t,AQ=5t,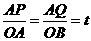 ,又∠PAQ=∠QAB,∴△APQ∽△AOB.
,又∠PAQ=∠QAB,∴△APQ∽△AOB.
∴∠APQ=∠AOB=90°。
∵点P在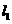 上,∴⊙Q在运动过程中保持与
上,∴⊙Q在运动过程中保持与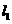 相切。
相切。
①当⊙Q在y轴右侧与y轴相切时,设 与⊙Q相切于F,由△APQ∽△AOB得
与⊙Q相切于F,由△APQ∽△AOB得
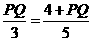 ,∴PQ=6,
,∴PQ=6,
连接QF,则QF=PQ, △QFC∽△APQ∽△AOB得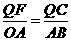 .
.
∴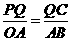 ,
,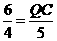 ,∴QC=
,∴QC=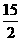 ,a=OQ+QC=
,a=OQ+QC=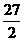 .
.
②当⊙Q在y轴左侧与y轴相切时,设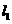 与⊙Q相切于E, 由△APQ∽△AOB得
与⊙Q相切于E, 由△APQ∽△AOB得
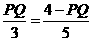 ,∴PQ=
,∴PQ=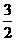 .
.
连接QE,则QE=PQ,由△QEC∽△APQ∽△AOB得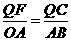 ,∴
,∴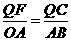 ,
,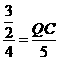 ,
,
∴QC=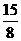 ,a=QC-OQ=
,a=QC-OQ=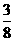 .∴a的值为
.∴a的值为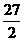 和
和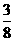 。
。
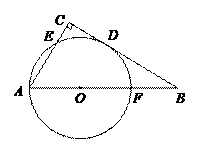
23. (2011江苏盐城,25,10分)如图,在△ABC中,∠C= 90°,以AB上一点O为圆心,OA长为半径的圆与BC相切于点D,分别交AC、AB于点E、F.
(1)若AC=6,AB= 10,求⊙O的半径;
(2)连接OE、ED、DF、EF.若四边形BDEF是平行四边形,试判断四边形OFDE的形状,并说明理由.
[答案](1)连接OD. 设⊙O的半径为r.
∵BC切⊙O于点D,∴OD⊥BC.
∵∠C=90°,∴OD∥AC,∴△OBD∽△ABC.
∴ = ,即 = . 解得r = ,
∴⊙O的半径为.
(2)四边形OFDE是菱形.
∵四边形BDEF是平行四边形,∴∠DEF=∠B.
∵∠DEF=∠DOB,∴∠B=∠DOB.
∵∠ODB=90°,∴∠DOB+∠B=90°,∴∠DOB=60°.
∵DE∥AB,∴∠ODE=60°.∵OD=OE,∴△ODE是等边三角形.
∴OD=DE.∵OD=OF,∴DE=OF.∴四边形OFDE是平行四边形. 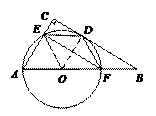
∵OE=OF,∴平行四边形OFDE是菱形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com