
题目列表(包括答案和解析)
14.
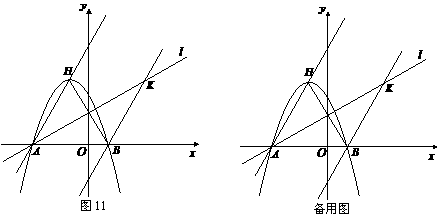
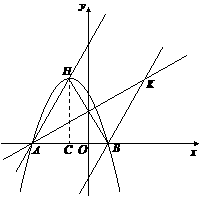
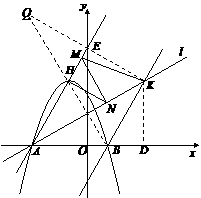
(2011福建福州,22,14分)已知,如图11,二次函数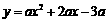
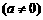 图象的顶点为
图象的顶点为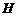 ,与
,与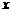 轴交于
轴交于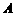 、
、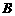 两点(
两点(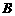 在
在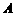 点右侧),点
点右侧),点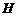 、
、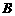 关于直线
关于直线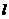 :
: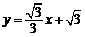 对称.
对称.
(1)求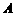 、
、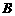 两点坐标,并证明点
两点坐标,并证明点 在直线
在直线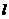 上;
上;
(2)求二次函数解析式;
(3)过点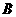 作直线
作直线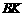 ∥
∥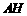 交直线
交直线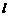 于
于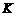 点,
点,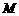 、
、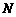 分别为直线
分别为直线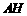 和直线
和直线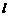 上的两个动点,连接
上的两个动点,连接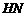 、
、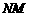 、
、 ,求
,求 和的最小值.
和的最小值.

[答案]解:(1)依题意,得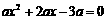
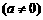
解得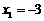 ,
,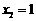
∵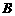 点在
点在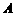 点右侧
点右侧
∴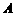 点坐标为
点坐标为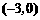 ,
,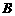 点坐标为
点坐标为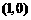
∵直线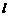 :
: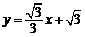
当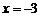 时,
时,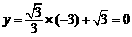
∴点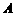 在直线
在直线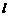 上
上

(2)∵点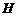 、
、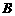 关于过
关于过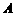 点的直线
点的直线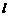 :
: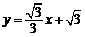 对称
对称
∴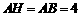
过顶点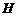 作
作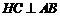 交
交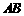 于
于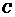 点
点
则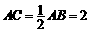 ,
,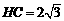
∴顶点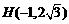
把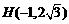 代入二次函数解析式,解得
代入二次函数解析式,解得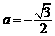
∴二次函数解析式为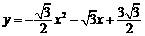
(3)直线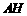 的解析式为
的解析式为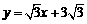
直线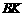 的解析式为
的解析式为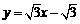
由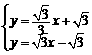 解得
解得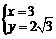 即
即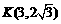 ,则
,则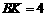
∵点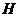 、
、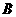 关于直线
关于直线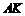 对称
对称
∴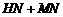 的最小值是
的最小值是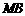 ,过
,过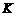 作
作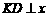 轴于D点。
轴于D点。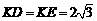
过点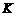 作直线
作直线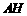 的对称点
的对称点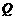 ,连接
,连接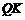 ,交直线
,交直线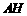 于
于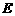
则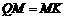 ,
,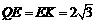 ,
,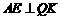
∴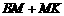 的最小值是
的最小值是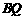 ,即
,即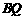 的长是
的长是 的最小值
的最小值
∵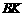 ∥
∥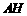
∴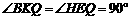
在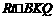 由勾股定理得
由勾股定理得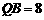
∴ 的最小值为
的最小值为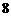
(不同解法参照给分)

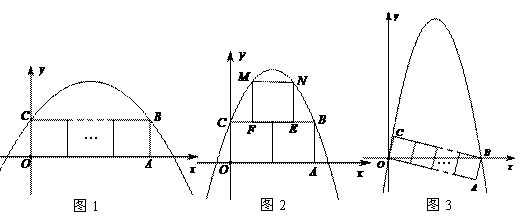
13. . (2011浙江金华,23,10分)在平面直角坐标系中,如图1,将n个边长为1的正方形并排组成矩形OABC,相邻两边OA和OC分别落在x轴和y轴的正半轴上,设抛物线y=ax2+bx+c(a<0)过矩形顶点B、C.
(1)当n=1时,如果a=-1,试求b的值;
(2)当n=2时,如图2,在矩形OABC上方作一边长为1的正方形EFMN,使EF在线段CB上,如果M,N两点也在抛物线上,求出此时抛物线的解析式;
(3)将矩形OABC绕点O顺时针旋转,使得点B落到x轴的正半轴上,如果该抛物线同时经过原点O,
①试求出当n=3时a的值;
②直接写出a关于n的关系式.

解:(1)由题意可知,抛物线对称轴为直线x=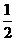 ,
,
∴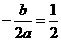 ,得
,得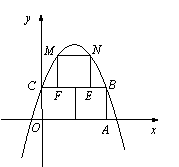 b= 1; ……2分
b= 1; ……2分
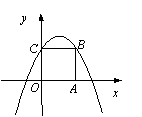 (2)设所求抛物线解析式为
(2)设所求抛物线解析式为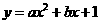 ,
,
由对称性可知抛物线经过点B(2,1)和点M(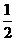 ,2)
,2)
∴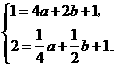 解得
解得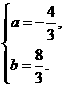
∴所求抛物线解析式为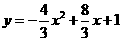 ;……4分
;……4分
(3)①当n=3时,OC=1,BC=3,
设所求抛物线解析式为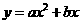 ,
,
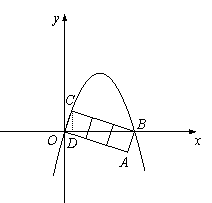 过C作CD⊥OB于点D,则Rt△OCD∽Rt△CBD,
过C作CD⊥OB于点D,则Rt△OCD∽Rt△CBD,
∴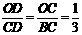 ,
,
设OD=t,则CD=3t,
∵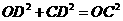 ,
,
∴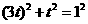 , ∴
, ∴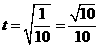 ,
,
∴C(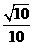 ,
,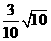 ), 又 B(
), 又 B(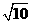 ,0),
,0),
∴把B 、C坐标代入抛物线解析式,得
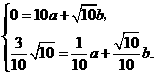 解得:a=
解得:a=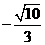 ; ……2分
; ……2分
②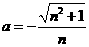 . ……2分
. ……2分
12. (2011湖北荆州,23,10分)(本题满分10分)2011年长江中下游地区发生了特大旱情,为抗旱保丰收,某地政府制定民农户投资购买抗旱设备的补贴办法,其中购买Ⅰ型、Ⅱ型抗旱设备所投资的金额与政府补贴的额度存在下表所示的函数对应关系.
|
型
号 金 额 |
Ⅰ型设备 |
Ⅱ型设备 |
|||
|
投资金额x(万元) |
x |
5 |
x |
2 |
4 |
|
补贴金额y(万元) |
y1=kx (k≠0) |
2 |
y2=ax2+bx (a≠0) |
2.4 |
3.2 |
(1)分别求出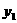 和
和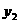 的函数解析式;
的函数解析式;
(2)有一农户同时对Ⅰ型、Ⅱ型两种设备共投资10万元购买,请你设计一个能获得最大补贴金额的方案,并求出按此方案能获得的最大补贴金额.
[答案]解:(1)由题意得:①5k=2,k=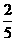
∴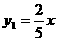
②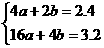 ,解之得:
,解之得: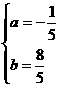 ,∴
,∴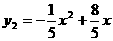
(2)设购Ⅱ型设备投资t万元,购Ⅰ型设备投资(10-t)万元,共获补贴Q万元
∴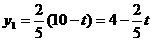 ,
,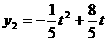
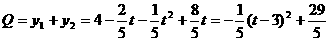
∴当t=3时,Q有最大值为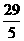 ,此时10-t=7(万元)
,此时10-t=7(万元)
即投资7万元购Ⅰ型设备,投资3万元购Ⅱ型设备,共获最大补贴5.8万元.
11. (2011湖北鄂州,23,12分)我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润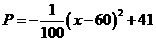 (万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润
(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润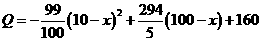 (万元)
(万元)
⑴若不进行开发,求5年所获利润的最大值是多少?
⑵若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
⑶根据⑴、⑵,该方案是否具有实施价值?
[答案]解:⑴当x=60时,P最大且为41,故五年获利最大值是41×5=205万元.
⑵前两年:0≤x≤50,此时因为P随x增大而增大,所以x=50时,P值最大且为40万元,所以这两年获利最大为40×2=80万元.
后三年:设每年获利为y,设当地投资额为x,则外地投资额为100-x,所以y=P+Q
=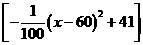 +
+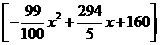 =
=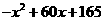 =
=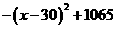 ,表明x=30时,y最大且为1065,那么三年获利最大为1065×3=3495万元,
,表明x=30时,y最大且为1065,那么三年获利最大为1065×3=3495万元,
故五年获利最大值为80+3495-50×2=3475万元.
⑶有极大的实施价值.
10.(2011江苏盐城,26,10分)利民商店经销甲、乙两种商品. 现有如下信息:


请根据以上信息,解答下列问题:
(1)甲、乙两种商品的进货单价各多少元?
(2)该商店平均每天卖出甲商品500件和乙商品300件.经调查发现,甲、乙两种商品零售单价分别每降0.1元,这两种商品每天可各多销售100件.为了使每天获取更大的利润,商店决定把甲、乙两种商品的零售单价都下降m元. 在不考虑其他因素的条件下,当m定为多少时,才能使商店每天销售甲、乙两种商品获取的利润最大?每天的最大利润是多少?
[答案](1)设甲商品的进货单价是x元,乙商品的进货单价是y元.
根据题意,得 解得
答:甲商品的进货单价是2元,乙商品的进货单价是3元.
(2)设商店每天销售甲、乙两种商品获取的利润为s元,则
s=(1-m)(500+100×)+(5-3-m)(300+100×)
即 s=-2000m2+2200m+1100 =-2000(m-0.55)2+1705.
∴当m=0.55时,s有最大值,最大值为1705.
答:当m定为0.55时,才能使商店每天销售甲、乙两种商品获取的利润最大,每天的最大利润是1705元.
9. (2011贵州贵阳,25,12分)
用长度一定的不锈钢材料设计成外观为矩形的框架(如图123中的一种).
设竖档AB=x米,请根据以上图案回答下列问题:(题中的不锈钢材料总长度均指各图中所有黑线的长度和,所有横档和竖档分别与AD、AB平行)
(1)在图1中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积为3平方米?(4分)
(2)在图2中,如果不锈钢材料总长度为12米,当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?(4分)
(3)在图3中,如果不锈钢材料总长度为a米,共有n条竖档,那么当x为多少时,矩形框架ABCD的面积S最大?最大面积是多少?
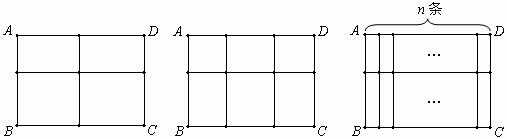
1 2 3
(第25题图)
[答案]解:
(1)当不锈钢材料总长度为12米,共有3条竖档时,BC==4-x,
∴x(4-x)=3.
解得,x=1或3.
(2)当不锈钢材料总长度为12米,共有4条竖档时,BC=,矩形框架ABCD的面积S=x·=-x2+4x.
当x=-=时,S=3.
∴当x=时时,矩形框架ABCD的面积S最大,最大面积为3平方米.
(3)当不锈钢材料总长度为a米,共有n条竖档时,BC=,矩形框架ABCD的面积
S=x·=-x2+x.
当x=-=时,S=
∴当x=时,矩形框架ABCD的面积S最大,最大面积为平方米
8. (2011湖北黄冈,23,12分)我市某镇的一种特产由于运输原因,长期只能在当地销售.当地政府对该特产的销售投资收益为:每投入x万元,可获得利润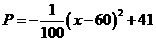 (万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润
(万元).当地政府拟在“十二•五”规划中加快开发该特产的销售,其规划方案为:在规划前后对该项目每年最多可投入100万元的销售投资,在实施规划5年的前两年中,每年都从100万元中拨出50万元用于修建一条公路,两年修成,通车前该特产只能在当地销售;公路通车后的3年中,该特产既在本地销售,也在外地销售.在外地销售的投资收益为:每投入x万元,可获利润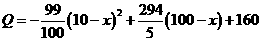 (万元)
(万元)
⑴若不进行开发,求5年所获利润的最大值是多少?
⑵若按规划实施,求5年所获利润(扣除修路后)的最大值是多少?
⑶根据⑴、⑵,该方案是否具有实施价值?
[答案]解:⑴当x=60时,P最大且为41,故五年获利最大值是41×5=205万元.
⑵前两年:0≤x≤50,此时因为P随x增大而增大,所以x=50时,P值最大且为40万元,所以这两年获利最大为40×2=80万元.
后三年:设每年获利为y,设当地投资额为x,则外地投资额为100-x,所以y=P+Q
=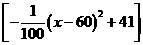 +
+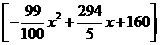 =
=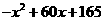 =
=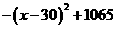 ,表明x=30时,y最大且为1065,那么三年获利最大为1065×3=3495万元,
,表明x=30时,y最大且为1065,那么三年获利最大为1065×3=3495万元,
故五年获利最大值为80+3495-50×2=3475万元.
⑶有极大的实施价值.
7. (2011湖北武汉市,23,10分)(本题满分10分)星光中学课外活动小组准备围建一个矩形生物苗圃园.其中一边靠墙,另外三边用长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边的长为x米.
(1)若平行于墙的一边的长为y米,直接写出y与x之间的函数关系式及其自变量x的取值范围;
(2)垂直于墙的一边的长为多少米时,这个苗圃园的面积最大,并求出这个最大值;
(3)当这个苗圃园的面积不小于88平方米时,试结合函数图像,直接写出x的取值范围.
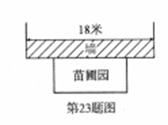
[答案]解:(1)y=30-2x(6≤x<15)
(2)设矩形苗圃园的面积为S则S=xy=x(30-2x)=-2x2+30x
∴S=-2(x-7.5)2+112.5由(1)知,6≤x<15∴当x=7.5时,S最大值=112.5
即当矩形苗圃园垂直于墙的边长为7.5米时,这个苗圃园的面积最大,最大值为112.5
(3)6≤x≤11
6. (2011江苏无锡,25,10分)(本题满分10分)张经理到老王的果园里一次性采购一种水果,他俩商定:张经理的采购价y (元/吨)与采购量x (吨)之间函数关系的图象如图中的折线段ABC所示(不包含端点A,但包含端点C)。
(1)求y与x之间的函数关系式;
(2)已知老王种植水果的成本是2800元/吨,那么张经理的采购量为多少时,老王在这次买卖中所获的利润w最大?最大利润是多少?


[答案]
解:(1)当0 < x ≤ 20时,y = 8000.……………………………………………………(1分)
当20 < x ≤ 40时,设BC满足的函数关系式为y = kx + b,则 .………………(2分)
解得k = −200,b = 12 000,∴y = −200x + 12 000. ………………………………(4分)
(2)当0 < x ≤ 20时,老王获得的利润为w = (8000 − 2800)x …………(5分)
=5 200x ≤ 104 000,此时老王获得的最大利润为104 000元.…………(6分)
当20 < x ≤ 40时,老王获得的利润为w = (−200x + 12 000 − 2800)x ………………(7分)
= −200(x2 − 46x) = −200(x − 23)2 + 105 800.………………………………(8分)
∴当x = 23时,利润w取得最大值,最大值为105 800元.………………………(9分)
∵105 800 > 104 000,∴当张经理的采购量为23吨时,老王在这次买卖中所获得的利润最大,最大利润为105 800元.………………………………………………………(10分)
4. (2011四川成都,26,8分)某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围).当x为何值时,S取得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为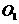 和
和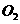 ,且
,且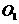 到AB、BC、AD的距离与
到AB、BC、AD的距离与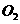 到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最大值时,请问这
到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最大值时,请问这 个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.
个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.
[答案](1)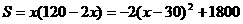 ,当
,当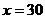 时,S取最大值为1800.
时,S取最大值为1800.
(2)如图所示,过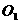 、
、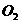 分别作到AB、BC、AD和CD、BC、AD的垂直,垂足如图,根据题意可知,
分别作到AB、BC、AD和CD、BC、AD的垂直,垂足如图,根据题意可知,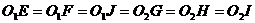 ;当S取最大值时,AB=CD=30,BC=60,
;当S取最大值时,AB=CD=30,BC=60,
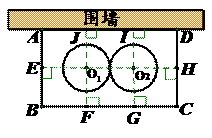 所以
所以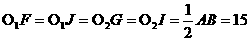 ,
,
∴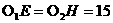 ,
,
∴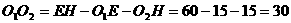 ,
,
∴两个等圆的半径为15,左右能够留0.5米的平直路面,而AD和BC与两圆相切,不能留0.5米的平直路面.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com