
题目列表(包括答案和解析)
8. 2011四川重庆,10,4分)如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④S△FGC=3.其中正确结论的个数是( )
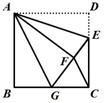
A.1 B.2 C.3 D.4
[答案]C
7. (2011浙江温州,6,4分)如图,在矩形ABCD中,对角线AC,BD交于点O.已知∠AOB= 60°,AC=16,则图中长度为8的线段有( )
A.2条 B.4条 C.5条 D.6条
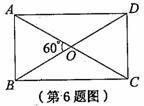
[答案]D
6. (2011浙江衢州,1,3分)衢州市新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡 分别架在墙体的点
分别架在墙体的点 、点
、点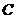 处,且
处,且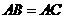 ,侧面四边形
,侧面四边形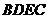 为矩形,若测得
为矩形,若测得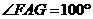 ,则
,则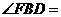 ( )
( )
A. 35° B. 40° C. 55° D. 70°

[答案]C
5. (2011浙江杭州,10,3)在矩形ABCD中,有一个菱形BFDE(点E,F分别在线段AB,CD上),记它们的面积分别
为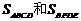 .现给出下列命题:( )
.现给出下列命题:( )
①若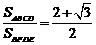 ,则
,则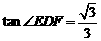 .②若
.②若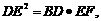 则
则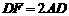 .
.
则:
A.①是真命题,②是真命题 B.①是真命题,②是假命题
C.①是假命题,②是真命题 D,①是假命题,②是假命题
[答案]A
4. (2011山东泰安,19 ,3分)如图,点O是矩形ABCD的中心,E是AB上的点,沿CE折叠后,点B恰好与点O重合,若BC=3,则折痕CE的长为
A.2
B. C.
D.6 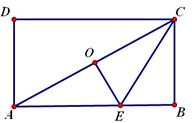
[答案]A
3. (2011山东泰安,17 ,3分)如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为
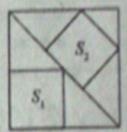
A.17 B.17 C.18 D.19
[答案]B
2. (2011山东德州8,3分)图1是一个边长为1的等边三角形和一个菱形的组合图形,菱形边长为等边三角形边长的一半,以此为基本单位,可以拼成一个形状相同但尺寸更大的图形(如图2),依此规律继续拼下去(如图3),……,则第n个图形的周长是
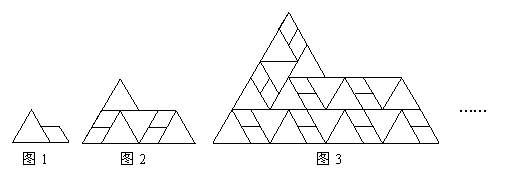
(A)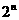 (B)
(B)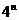 (C)
(C)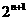 (D)
(D)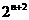
[答案]C
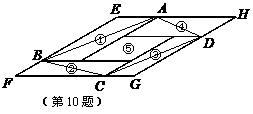
1. (2011浙江省舟山,10,3分)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )
(A)48cm (B)36cm
(C)24cm (D)18cm
[答案]A
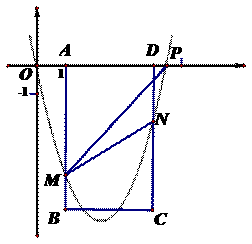
36. (2011河北,26,12分)如图15,在平面直角坐标系中,点P从原点O出发,沿x轴向右以每秒一个单位长的速度运动t秒(t>0),抛物线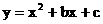 经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).
经过点O和点P.已知矩形ABCD的三个顶点为A(1,0),B(1,-5),D(4,0).
(1)求c,b(用t的代数式表示);
(2)当4<t<5时,设抛物线分别与线段AB,CD交于点M,N.
①在点P的运动过程中,你认为∠AMP的大小是否会变化?若变化,说明理由;若不变,求出∠AMP的值;
②求△MPN的面积S与t的函数关系式,并求t为何值时,s=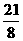 ;
;
(3)在矩形ABCD内部(不含边界),把横纵坐标都是整数的点称为“好点”.若抛物线将这些“好点”分成数量相等的两部分,请直接写出t的取值范围。
[答案](1)C=0,b=-t
(2)①不变。当x=1时,y=1-t,故M(1,1-t),∵tan∠AMP=1,∴∠AMP=45°。
②S=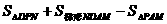
=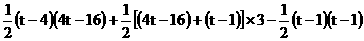
=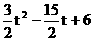
解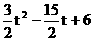 =
=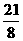 ,得
,得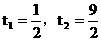
∵4<t<5,∴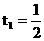 舍去,∴t=
舍去,∴t=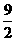
(3)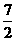 <t<
<t<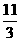
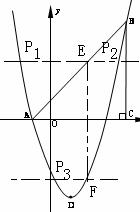
35. (2011重庆市潼南,26,12分)如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,
OC=4,抛物线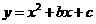 经过A,B两点,抛物线的顶点为D.
经过A,B两点,抛物线的顶点为D.
(1)求b,c的值;
(2)点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线
交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上
是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的
坐标;若不存在,说明理由.
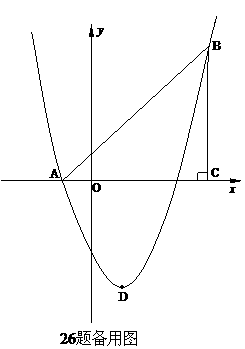
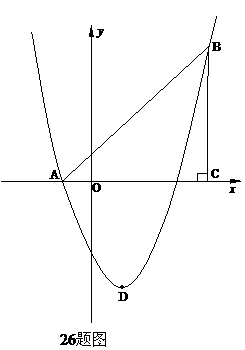
[答案]解:(1)由已知得:A(-1,0) B(4,5)------------1分
 ∵二次函数
∵二次函数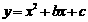 的图像经过点A(-1,0)B(4,5)
的图像经过点A(-1,0)B(4,5)
∴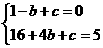 ------------2分
------------2分
解得:b=-2 c=-3 ------------3分
(2如26题图:∵直线AB经过点A(-1,0) B(4,5)
∴直线AB的解析式为:y=x+1
∵二次函数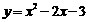
∴设点E(t, t+1),则F(t,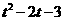 ) ------------4分
) ------------4分
∴EF= 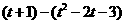 ------------5分
------------5分
=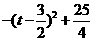
 ∴当
∴当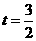 时,EF的最大值=
时,EF的最大值=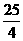
∴点E的坐标为(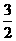 ,
,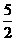 ) ------------------------6分
) ------------------------6分
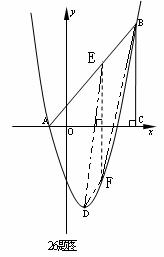
(3)①如26题图:顺次连接点E、B、F、D得四边形EBFD.
可求出点F的坐标(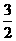 ,
,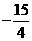 ),点D的坐标为(1,-4)
),点D的坐标为(1,-4)
S = S
= S + S
+ S
=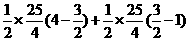
|
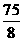 -----------------------------------9分
-----------------------------------9分
②如26题备用图:ⅰ)过点E作a⊥EF交抛物线于点P,设点P(m,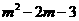 )
)
则有: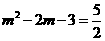 解得:
解得: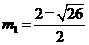 ,
,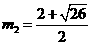
∴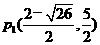 ,
, 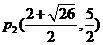
ⅱ)过点F作b⊥EF交抛物线于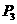 ,设
,设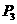 (n,
(n,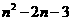 )
)
则有: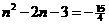 解得:
解得: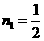 ,
,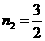 (与点F重合,舍去)∴
(与点F重合,舍去)∴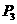
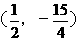
综上所述:所有点P的坐标: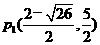 ,
,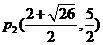
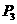 (
(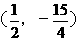 . 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
. 能使△EFP组成以EF为直角边的直角三角形.------------------------------------12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com