
题目列表(包括答案和解析)
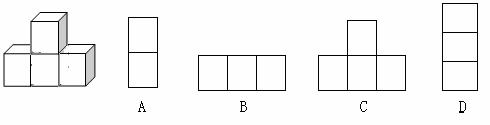
4、由4个大小相同的正方体组成的几何体如图所示,那么它的俯视图是( )
3、下列运算正确的是( )
A 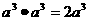 B
B 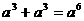 C
C 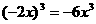 D
D 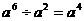
2、光的传播速度为300000km/s,该数用科学记数法表示为( )
A 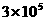 B
B 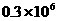 C
C 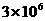 D
D 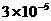
1、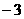 的相反数是( )
的相反数是( )
A 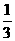 B
B 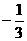 C 3 D
C 3 D 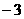
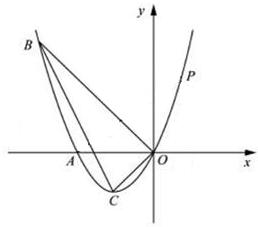
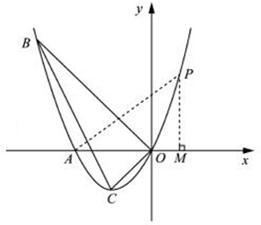
26、(2011•临沂)如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.
(1)求抛物线的解析式;
(2)若点D在抛物线上,点E在抛物线的对称轴上,且A、O、D、E为顶点的四边形是平行四边形,求点D的坐标;
(3)P是抛物线上的第一象限内的动点,过点P作PMx轴,垂足为M,是否存在点P,使得以P、M、A为顶点的三角形△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题。
专题:综合题。
分析:(1)由于抛物线经过A(﹣2,0),B(﹣3,3)及原点O,待定系数法即可求出抛物线的解析式;
(2)根据平行四边形的性质,对边平行且相等以及对角线互相平方,可以求出点D的坐标;
(3)根据相似三角形对应边的比相等可以求出点P的坐标.
解答:解(1)设抛物线的解析式为y=ax2+bx+c(a≠0),且过A(﹣2,0),B(﹣3,3),O(0,0)可得
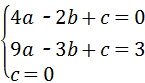 ,
,
解得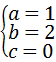 .
.
故抛物线的解析式为y=x2+2x;
(2)①当AE为边时,
∵A、O、D、E为顶点的四边形是平行四边形,
∴DE=AO=2,
则D在x轴下方不可能,
∴D在x轴上方且DE=2,
则D1(1,3),D2(﹣3,3);
②当AO为对角线时,则DE与AO互相平方,
因为点E在对称轴上,
且线段AO的中点横坐标为﹣1,
由对称性知,符合条件的点D只有一个,与点C重合,即C(﹣1,﹣1)
故符合条件的点D有三个,分别是D1(1,3),D2(﹣3,3),C(﹣1,﹣1);
(3)存在,
如上图:∵B(﹣3,3),C(﹣1,﹣1),根据勾股定理得:
BO2=18,CO2=2,BC2=20,
∴BO2+CO2=BC2.
∴△BOC是直角三角形.
假设存在点P,使以P,M,A为顶点的 三角形与△BOC相似,
设P(x,y),由题意知x>0,y>0,且y=x2+2x,
①若△AMP∽△BOC,则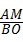 =
=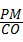 ,
,
即 x+2=3(x2+2x)
得:x1=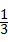 ,x2=﹣2(舍去).
,x2=﹣2(舍去).
当x=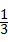 时,y=
时,y=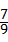 ,即P(
,即P(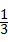 ,
,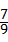 ).
).
②若△PMA∽△BOC,则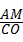 =
=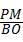 ,
,
即:x2+2x=3(x+2)
得:x1=3,x2=﹣2(舍去)
当x=3时,y=15,即P(3,15).
故符合条件的点P有两个,分别是P(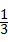 ,
,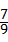 )或(3,15).
)或(3,15).
点评:本题考查的是二次函数的综合题,首先用待定系数法求出抛物线的解析式,然后利用平行四边形的性质和相似三角形的性质确定点D和点P的坐标.
25、(2011•临沂)如图1,将三角板放在正方形ABCD上,使三角板的直角顶点E与正方形ABCD的顶点A重合,三角扳的一边交CD于点F.另一边交CB的延长线于点G.
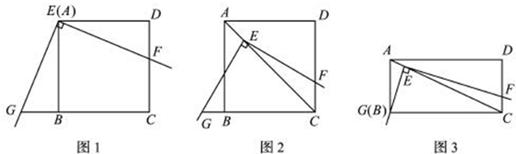
(1)求证:EF=EG;
(2)如图2,移动三角板,使顶点E始终在正方形ABCD的对角线AC上,其他条件不变,(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理由:
(3)如图3,将(2)中的“正方形ABCD”改为“矩形ABCD”,且使三角板的一边经过点B,其他条件不变,若AB=a、BC=b,求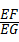 的值.
的值.
考点:相似三角形的判定与性质;全等三角形的判定与性质;矩形的性质;正方形的性质。
分析:(1)由∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,可得∠DEF=∠GEB,又由正方形的性质,可利用SAS证得Rt△FED≌Rt△GEB,则问题得证;
(2)首先点E分别作BC、CD的垂线,垂足分别为H、I,然后利用SAS证得Rt△FEI≌Rt△GEH,则问题得证;
(3)首先过点E分别作BC、CD的垂线,垂足分别为M、N,易证得EM∥AB,EN∥AD,则可证得△CEN∽△CAD,△CEM∽△CAB,又由有两角对应相等的三角形相似,证得△GME∽△FNE,根据相似三角形的对应边成比例,即可求得答案.
解答:(1)证明:∵∠GEB+∠BEF=90°,∠DEF+∠BEF=90°,
∴∠DEF=∠GEB,
又∵ED=BE,
∴Rt△FED≌Rt△GEB,
∴EF=EG;
(2)成立.
证明:如图,过点E分别作BC、CD的垂线,垂足分别为H、I,
则EH=EI,∠HEI=90°,
∵∠GEH+∠HEF=90°,∠IEF+∠HEF=90°,
∴∠IEF=∠GEH,
∴Rt△FEI≌Rt△GEH,
∴EF=EG;
(3)解:如图,过点E分别作BC、CD的垂线,垂足分别为M、N,
则∠MEN=90°,
∴EM∥AB,EN∥AD.
∴△CEN∽△CAD,△CEM∽△CAB,
∴ ,
,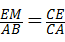 ,
,
∴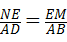 ,即
,即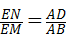 =
=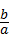 ,
,
∵∠IEF+∠FEM=∠GEM+∠FEM=90°,
∴∠GEM=∠FEN,
∵∠GME=∠FNE=90°,
∴△GME∽△FNE,
∴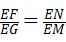 ,
,
∴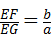 .
.
点评:此题考查了正方形,矩形的性质,以及全等三角形与相似三角形的判定与性质.此题综合性较强,注意数形结合思想的应用.
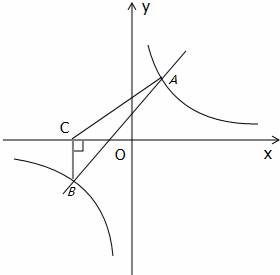
24、(2011•临沂)如图,一次函数y=kx+b与反比例函数y=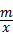 的图象相较于A(2,3),B(﹣3,n)两点.
的图象相较于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)根据所给条件,请直接写出不等式kx+b>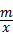 的解集;
的解集;
(3)过点B作BC⊥x轴,垂足为C,求S△ABC.
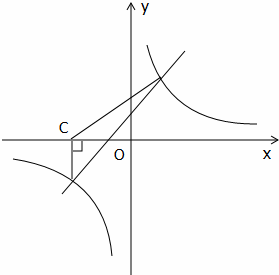
考点:反比例函数与一次函数的交点问题。
分析:(1)由一次函数y=kx+b与反比例函数y=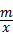 的图象相较于A(2,3),B(﹣3,n)两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
的图象相较于A(2,3),B(﹣3,n)两点,首先求得反比例函数的解析式,则可求得B点的坐标,然后利用待定系数法即可求得一次函数的解析式;
(2)根据图象,观察即可求得答案;
(3)因为以BC为底,则BC边上的高为3+2=5,所以利用三角形面积的求解方法即可求得答案.
解答:解:(1)∵点A(2,3)在y=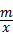 的图象上,
的图象上,
∴m=6,
∴反比例函数的解析式为:y=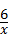 ,
,
 ∴n=
∴n=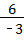 =﹣2,
=﹣2,
∵A(2,3),B(﹣3,﹣2)两点在y=kx+b上,
∴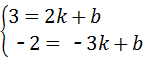 ,
,
解得: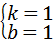 ,
,
∴一次函数的解析式为:y=x+1;
(2)﹣3<x<0或x>2;
(3)以BC为底,则BC边上的高为3+2=5,
∴S△ABC=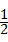 ×2×5=5.
×2×5=5.
点评:此题考查了反比例函数与一次函数的交点问题.注意待定系数法的应用是解题的关键.
23、(2011•临沂)如图.以O为圆心的圆与△AOB的边AB相切于点C.与OB相交于点D,且OD=BD,己知sinA=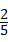 ,AC=
,AC=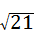 .
.
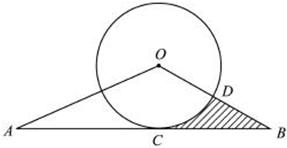
(1)求⊙O的半径:
(2)求图中阴影部分的面枳.
考点:切线的性质;扇形面积的计算;解直角三角形。
分析:(1)根据切线的性质得出CO⊥AB,再根据解直角三角形得出CO,AO的关系,进而得出它们的长度,即可得出半径长度;
(2)根据已知得出∠COD=60°,进而利用三角形面积减去扇形面积即可得出答案.
解答:解: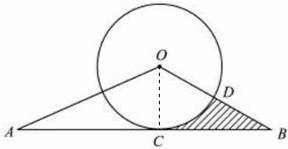 (1)连接OA,
(1)连接OA,
∵以O为圆心的圆与△AOB的边AB相切于点C.
∴CO⊥AB,
∵sinA=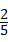 =
=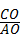 ,
,
∵AC=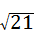 .
.
∴假设CO=2x,AO=5x,
4x2+21=25x2,
解得:x=1,
∴CO=2,
∴⊙O的半径为2;
(2)∵⊙O的半径为2;
∴DO=2,
∵DO=DB,
∴BO=4,
∴BC=2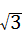 ,
,
∴2CO=BO,
∵O⊥BC,
∴∠CBO=30°,
∠COD=60°,
图中阴影部分的面枳为:S△OCB﹣S扇形COD=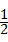 ×2
×2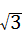 ×2﹣
×2﹣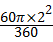 =2
=2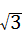 ﹣
﹣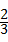 π.
π.
点评:此题主要考查了扇形面积求法以及切线的性质和勾股定理的应用等知识,得出图中阴影部分的面枳为:S△OCB﹣S扇形COD是解决问题的关键.
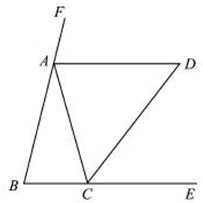
22、(2011•临沂)如图,△ABC中,AB=AC,AD、CD分別是△ABC两个外角的平分线.
(1)求证:AC=AD;
(2)若∠B=60°,求证:四边形ABCD是菱形.
考点:菱形的判定;等腰三角形的判定与性质。
专题:证明题。
分析:(1)根据角平分线的性质得出∠FAD=∠B,以及AD∥BC,再利用∠D=∠ACD,证明AC=AD;
(2)根据平行四边形的判定方法得出四边形ABCD是平行四边形,再利用菱形的判定得出.
解答:证明:(1)∵AB=AC,
∴∠B=∠BCA,
∵AD平分∠FAC,
∴∠FAD=∠B,
∴AD∥BC,
∴∠D=∠DCE,
∵CD平分∠ACE,
∴∠ACD=∠DCE,
∴∠D=∠ACD,
∴AC=AD;
证明:(2)∵∠B=60°,AB=AC,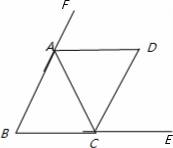
∴△ABC为等边三角形,
∴AB=BC,
∴∠ACB=60°,
∠FAC=∠ACE=120°,
∴∠BAD=∠BCD=120°,
∴∠B=∠D=60°,
∴四边形ABCD是平行四边形,
∵AB=BC,
∴平行四边形ABCD是菱形.

点评:此题主要考查了平行四边形的判定以及菱形的判定和角平分线的性质等内容,注意菱形与平行四边形的区别,得出AB=BC是解决问题的关键.
21、(2011•临沂)去年秋季以来,我市某镇遭受百年一遇的特大旱灾,为支援该镇抗旱,上级下达专项抗旱资金80万元用于打井,已知用这80万元打灌溉用井和生活用井共58口,每口灌溉用井和生活用井分别需要资金4万元和0.2万元,求这两种井各打多少口?
考点:二元一次方程组的应用。
分析:用二元一次方程组解决问题的关键是找到2个合适的等量关系.本题中2个等量关系为:打灌溉用井和生活用井共58口;用这80万元打灌溉用井和生活用井.
解答:解:灌溉用井打x口,生活用井打y口,由题意得
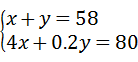 ,
,
解得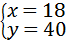 .
.
答:灌溉用井打18口,生活用井打40口.
点评:考查了二元一次方程组的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com