
题目列表(包括答案和解析)
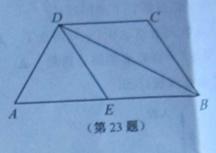
36. (20011江苏镇江,23,7分)已知:如图,在梯形ABCD中AB∥CD,BC=CD,AD⊥BD,E为AB中点,
求证:四边形BCDE是菱形.
答案:证明:∵AD⊥BD,
∴∠ADB=90°。
又E为AB中点,∴DE=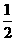 AB,BE=
AB,BE=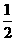 AB, ∴DE=BE
AB, ∴DE=BE
∴∠ DBE =∠EDB
又AB∥CD, ∴∠ BDC =∠EDB
∵BC=CD, ∴∠DBC =∠DBC
∴BC∥DE.
∵EB∥CD
∴四边形BCDE是平行四边形
∵BC=CD
∴四边形BCDE是菱形。
35. (2011江苏盐城,27,12分)
情境观察
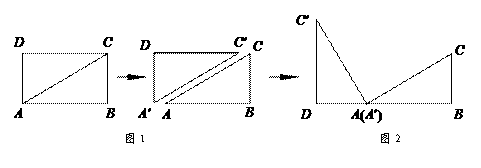
将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示.将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
观察图2可知:与BC相等的线段是 ▲ ,∠CAC′= ▲ °.

问题探究
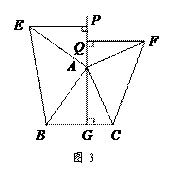
如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q. 试探究EP与FQ之间的数量关系,并证明你的结论.

拓展延伸
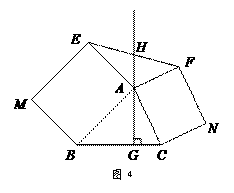
如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H. 若AB= k AE,AC= k AF,试探究HE与HF之间的数量关系,并说明理由.

[答案]情境观察
AD(或A′D),90
问题探究
结论:EP=FQ.
证明:∵△ABE是等腰三角形,∴AB=AE,∠BAE=90°.
∴∠BAG+∠EAP=90°.∵AG⊥BC,∴∠BAG+∠ABG=90°,∴∠ABG=∠EAP.
∵EP⊥AG,∴∠AGB=∠EPA=90°,∴Rt△ABG≌Rt△EAP. ∴AG=EP.
同理AG=FQ. ∴EP=FQ.
拓展延伸
结论: HE=HF.
理由:过点E作EP⊥GA,FQ⊥GA,垂足分别为P、Q.

∵四边形ABME是矩形,∴∠BAE=90°,
∴∠BAG+∠EAP=90°.AG⊥BC,∴∠BAG+∠ABG=90°,
∴∠ABG=∠EAP.
∵∠AGB=∠EPA=90°,∴△ABG∽△EAP,∴ = .
同理△ACG∽△FAQ,∴ = .
∵AB= k AE,AC= k AF,∴ = = k,∴ = . ∴EP=FQ.
∵∠EHP=∠FHQ,∴Rt△EPH≌Rt△FQH. ∴HE=HF.
34. (2011湖南永州,25,10分)探究问题:
⑴方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
将△ADE绕点A顺时针旋转90°得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=45° ∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2, ∴∠1+∠3=45°.
即∠GAF=∠_________.
又AG=AE,AF=AF
∴△GAF≌_______.
∴_________=EF,故DE+BF=EF.


⑵方法迁移:
如图②,将 沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=
沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠EAF=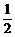 ∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.
∠DAB.试猜想DE,BF,EF之间有何数量关系,并证明你的猜想.


⑶问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足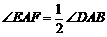 ,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).
,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).


[答案]⑴EAF、△EAF、GF.
⑵DE+BF=EF,理由如下:
假设∠BAD的度数为 ,将△ADE绕点A顺时针旋转
,将△ADE绕点A顺时针旋转 得到△ABG,此时AB与AD重合,由旋转可得:
得到△ABG,此时AB与AD重合,由旋转可得:
AB=AD,BG=DE, ∠1=∠2,∠ABG=∠D=90°,
∴∠ABG+∠ABF=90°+90°=180°,
因此,点G,B,F在同一条直线上.
∵∠EAF=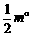 ∴∠2+∠3=∠BAD-∠EAF=
∴∠2+∠3=∠BAD-∠EAF=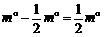
∵∠1=∠2, ∴∠1+∠3=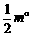 .
.
即∠GAF=∠EAF
又AG=AE,AF=AF
∴△GAF≌△EAF.
∴GF=EF,
又∵GF=BG+BF=DE+BF ∴DE+BF=EF.


⑶当∠B与∠D互补时,可使得DE+BF=EF.
33. (2011湖北襄阳,25,10分)
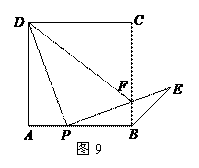
如图9,点P是正方形ABCD边AB上一点(不与点A,B重合),连接PD并将线段PD绕点P顺时针方向旋转90°得到线段PE,PE交边BC于点F,连接BE,DF.
(1)求证:∠ADP=∠EPB;
(2)求∠CBE的度数;
(3)当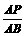 的值等于多少时,△PFD∽△BFP?并说明理由.
的值等于多少时,△PFD∽△BFP?并说明理由.

[答案]
(1)证明:∵四边形ABCD是正方形
∴∠A=∠PBC=90°,AB=AD,∴∠ADP+∠APD=90°················ 1分
∵∠DPE=90° ∴∠APD+∠EPB=90°
∴∠ADP=∠EPB.········································································································ 2分
(2)过点E作EG⊥AB交AB的延长线于点G,则∠EGP=∠A=90°·· 3分
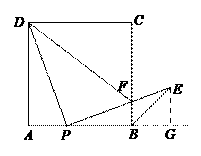
又∵∠ADP=∠EPB,PD=PE,∴△PAD≌△EGP
∴EG=AP,AD=AB=PG,∴AP=EG=BG················································· 4分
∴∠CBE=∠EBG=45°.························································································· 5分
(3)方法一:
当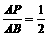 时,△PFE∽△BFP.·············································································· 6分
时,△PFE∽△BFP.·············································································· 6分
∵∠ADP=∠FPB,∠A=∠PBF,∴△ADP∽△BPF······························ 7分
设AD=AB=a,则AP=PB=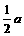 ,∴BF=BP·
,∴BF=BP·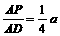 ···················· 8分
···················· 8分
∴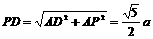 ,
,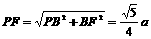
∴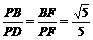 ··········································································································· 9分
··········································································································· 9分
又∵∠DPF=∠PBF=90°,∴△ADP∽△BFP·········································· 10分
方法二:
假设△ADP∽△BFP,则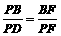 .·································································· 6分
.·································································· 6分
∵∠ADP=∠FPB,∠A=∠PBF,∴△ADP∽△BPF··························· 7分
∴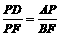 ,··············································································································· 8分
,··············································································································· 8分
∴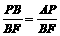 ,··············································································································· 9分
,··············································································································· 9分
∴PB=AP, ∴当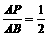 时,△PFE∽△BFP. 10分
时,△PFE∽△BFP. 10分
32. (2011广东肇庆,22,8分)如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为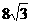 ,求AC的长.
,求AC的长.


[答案]解:(1)证明:∵DE∥OC ,CE∥OD,∴四边形OCED是平行四边形.
∵四边形ABCD是矩形 ∴ AO=OC=BO=OD
∴四边形OCED是菱形.


(2)∵∠ACB=30° ∴∠DCO = 90°- 30°= 60°
又∵OD= OC, ∴△OCD是等边三角形
过D作DF⊥OC于F,则CF=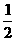 OC,设CF=
OC,设CF=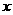 ,则OC= 2
,则OC= 2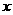 ,AC=4
,AC=4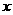
在Rt△DFC中,tan 60°=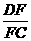 ∴DF=FC× tan 60°
∴DF=FC× tan 60°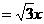
由已知菱形OCED的面积为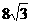 得OC× DF=
得OC× DF=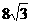 ,即
,即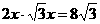 ,
,
解得 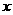 =2,
∴ AC=4´2=8
=2,
∴ AC=4´2=8
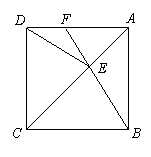
31. (2011广东肇庆,20,7分)如图,在正方形ABCD中,E为对角线AC上一点,连接EB、ED.
(1)求证:△BEC≌△DEC;
(2)延长BE交AD于点F,若∠DEB = 140°,求∠AFE的度数.

[答案]解:(1)证明:∵四边形ABCD 是正方形 ∴CD=CB,
∵AC是正方形的对角线 ∴∠DCA=∠BCA
又 CE = CE ∴△BEC≌△DEC
(2)∵∠DEB = 140°
由△BEC≌△DEC可得∠DEC =∠BEC=140°¸2=70°,
∴∠AEF =∠BEC=70°,
又∵AC是正方形的对角线, ∠DAB=90° ∴∠DAC =∠BAC=90°¸2=45°,
在△AEF中,∠AFE=180°- 70°- 45°=65°
30. (2011贵州贵阳,18,10分)
如图,点E是正方形ABCD内一点,△CDE是等边三角形,连接EB、EA,延长BE交边AD于点F.
(1)求证:△ADE≌△BCE;(5分)
(2)求∠AFB的度数.(5分)
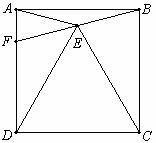
(第18题图)
[答案]解:(1)∵四边形ABCD是正方形,
∴∠ADC=∠BCD=90°,AD=BC.
∵△CDE是等边三角形,
∴∠CDE=∠DCE=60°,DE=CE.
∵∠ADC=∠BCD=90°,∠CDE=∠DCE=60°,
∴∠ADE=∠BCE=30°.
∵AD=BC,∠ADE=∠BCE,DE=CE,
∴△ADE≌△BCE.
(2)∵△ADE≌△BCE,
∴AE=BE,
∴∠BAE=∠ABE.
∵∠BAE+∠DAE=90°,∠ABE+∠AFB=90°,∠BAE=∠ABE,
∴∠DAE=∠AFB.
∵AD=CD=DE,
∴∠DAE=∠DEA.
∵∠ADE=30°,
∴∠DAE=75°,
∴∠AFB=75°.
29. (2011湖南衡阳,26,10分)如图,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连结PD,过点P作PQ⊥PD,交直线BC于点Q.
(1)当m=10时,是否存在点P使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由;
(2)连结AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示)
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.
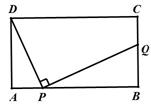
[解](1) 假设当m=10时,存在点P使得点Q与点C重合(如下图),
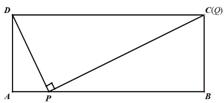
∵PQ⊥PD∴∠DPC=90°,∴∠APD+∠BPC=90°,
又∠ADP+∠APD=90°,∴∠BPC=∠ADP,
又∠B=∠A=90°,∴△PBC∽△DAP,∴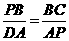 ,
,
∴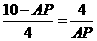 ,∴
,∴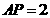 或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.
或8,∴存在点P使得点Q与点C重合,出此时AP的长2 或8.
(2) 如下图,∵PQ∥AC,∴∠BPQ=∠BAC,∵∠BPQ=∠ADP,∴∠BAC=∠ADP,又∠B=∠DAP=90°,∴△ABC∽△DAP,∴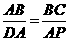 ,即
,即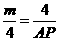 ,∴
,∴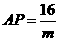 .
.
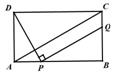
∵PQ∥AC,∴∠BPQ=∠BAC,∵∠B=∠B,∴△PBQ∽△ABC,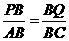 ,即
,即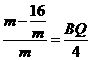 ,∴
,∴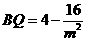 .
.
(3)由已知 PQ⊥PD,所以只有当DP=PQ时,△PQD为等腰三角形(如图),
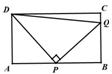
∴∠BPQ=∠ADP,又∠B=∠A=90°,∴△PBQ≌△DAP,
∴PB=DA=4,AP=BQ=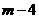 ,
,
∴以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为:S四边形PQCD= S矩形ABCD-S△DAP-S△QBP=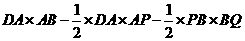
=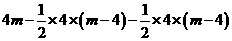 =16(4<
=16(4< ≤8).
≤8).
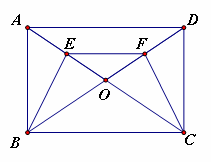
20.28. (2011四川乐山20,10分)如图,E、F分别是矩形ABCD的对角线AC和BD上的点,且AE=DF。求证:BE=CF
[答案]
证明:∵四边形ABCD为矩形
∴OA=OB=OC=OD AB=CD
∵AE=DF
∴OE=OF
在ΔBOE与ΔCOF中,
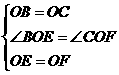
∴ΔBOE≌ΔCOF(SAS)
∴BE=CF
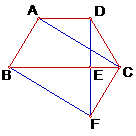
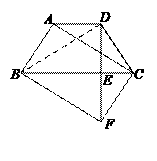
27. (2011上海,23,12分)如图,在梯形ABCD中,AD//BC,AB=DC,过点D作DE⊥BC,垂足为E,并延长DE至F,使EF=DE.联结BF、CF、AC.
(1)求证:四边形ABFC是平行四边形;
(2)如果DE2=BE·CE,求证四边形ABFC是矩形.
[答案](1)连接BD.
∵DE⊥BC,EF=DE,
∴BD=BF,CD=CF.
∵在梯形ABCD中,AD//BC,AB=DC,
∴四边形ABCD是等腰梯形.
∴BD=AC.
∴AC=BF,AB=CF.
∴四边形ABFC是平行四边形.

(2)∵DE2 =BE·CE,EF=DE,
∴EF2 =BE·CE.
∴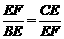 .
.
又∵DE⊥BC,
∴∠CEF=∠FEB=90°.
∴△CEF∽△FEB.
∴∠CFE=∠FBE.
∵∠FBE+∠BFE=90°,
∴∠CFE +∠BFE=90°.
即∠BFC=90°.
由(1)知四边形ABFC是平行四边形,
∴证四边形ABFC是矩形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com