
题目列表(包括答案和解析)
36. (2011四川重庆,17(1),3分)计算:|-3|+(-1)2011×(π-3)0-+()-2
[答案]原式=3+(-1)×1-3+4=3
35. (2011浙江省舟山,17,6分)计算: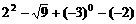 .
.
[答案]原式=4-3+1+2=4
34. (2011重庆綦江,17,6分) 计算:|―3|―(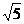 ―
―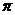 )
)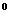 +
+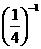 +(-1)3
+(-1)3
[答案]:17. 解:原式=3-1+4-1
=5
33. ( 2011重庆江津, 21(1),6分)( 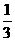 )-1-∣-2∣+2sin30º +(
)-1-∣-2∣+2sin30º +(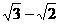 )º
)º
[答案](1) 原式=3-2+2×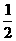 +1=3·
+1=3·
32. (2011四川内江,加试5,12分)同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2.但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道0×1+1×2+2×3+…+(n-1)×n=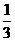 n(n+1)(n-1)时,我们可以这样做:
n(n+1)(n-1)时,我们可以这样做:
(1)观察并猜想:
12+22=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2)
12+22+32=(1+0)×1+(1+1)×2+(1+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
12+22+32+42=(1+0)×1+(1+1)×2+(1+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+( )
……
(2)归纳结论:
12+22+32+…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…+[1+(n-1)]n
=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n
=( ) +[ ]
= +
=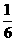 ×
×
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
[答案](1+3)×4
4+3×4
0×1+1×2+2×3+3×4
1+2+3+…+n
0×1+1×2+2×3++…+(n-1)×n
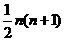
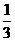 n(n+1)(n-1)
n(n+1)(n-1)
n(n+1)(2n+1)
31. (2011四川内江,17,7分)计算: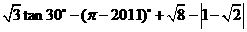
[答案]原式=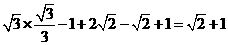
30. (2011四川广安,21,7分)计算: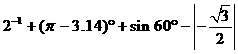
[答案]解:原式=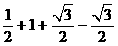 =
=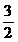
29. (2011四川成都,23,4分)设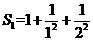 ,
,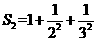 ,
,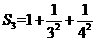 ,…,
,…, 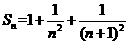
设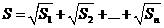 ,则S=_________ (用含n的代数式表示,其中n为正整数).
,则S=_________ (用含n的代数式表示,其中n为正整数).
[答案]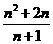 .
.
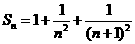 =
=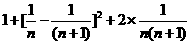 =
=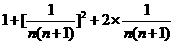
=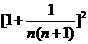
∴S=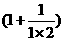 +
+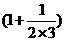 +
+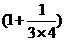 +…+
+…+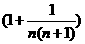
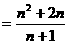 .
.
接下去利用拆项法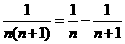 即可求和.
即可求和.
28. (2011四川成都,15(1),6分)(1)计算: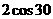 °
°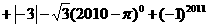 .
.
[答案]原式=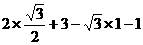
=2.
27. (2011江苏泰州,19(1),4分)计算或化简:
(1)
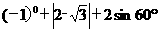 ;
;
[答案](1)原式=1+2-+2×=1+2-+=3
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com