
题目列表(包括答案和解析)
3.“投影”的概念:如图
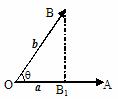
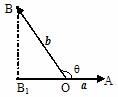
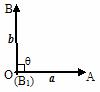
定义: _____|b|cosq_______叫做向量b在a方向上的投影
特别提醒:
投影也是一个数量,不是向量;当q为锐角时投影为正值;当q为钝角时投影为负值;当q为直角时投影为0;当q = 0°时投影为 |b|;当q = 180°时投影为 -|b|
2.平面向量数量积(内积)的定义:已知两个非零向量 与
与 ,它们的夹角是θ,则数量|
,它们的夹角是θ,则数量| ||
|| |cosq__叫
|cosq__叫 与
与 的数量积,记作
的数量积,记作 ×
× ,即有
,即有 ×
× = |
= | ||
|| |cosq
|cosq
特别提醒:
(1)
(0≤θ≤π).并规定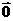 与任何向量的数量积为0
与任何向量的数量积为0
(2) 两个向量的数量积的性质:
设 、
、 为两个非零向量,
为两个非零向量,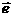 是与
是与 同向的单位向量
同向的单位向量
1)
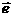 ×
× =
=  ×
×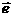 =|
=| |cosq;
|cosq;
2)
 ^
^ Û
Û  ×
× = 0
= 0
3)
当 与
与 同向时,
同向时, ×
× = |
= | ||
|| |;当
|;当 与
与 反向时,
反向时, ×
× = -|
= -| ||
|| |
|
特别的 ×
× = |
= | |2或
|2或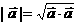
4)
cosq =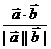 ;
;
5)
| ×
× | ≤ |
| ≤ | ||
|| |
|
1.两个非零向量夹角的概念
已知非零向量 与
与 ,作
,作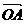 =
= ,
,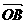 =
= ,则_∠AOB=θ(0≤θ≤π)叫
,则_∠AOB=θ(0≤θ≤π)叫 与
与 的夹角.
的夹角.
特别提醒:向量 与向量
与向量 要同起点。
要同起点。
10.已知点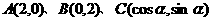 ,
, 为坐标原点,且
为坐标原点,且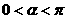 .
.
(1)若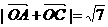 ,求
,求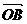 与
与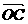 的夹角;
的夹角;
(2)若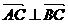 ,求tan
,求tan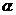 的值.
的值.
解:由已知可得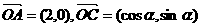 且
且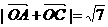 ……1分
……1分
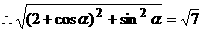
化简得: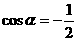 ……3分
……3分
因为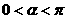
所以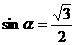 ……4分
……4分
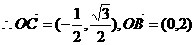
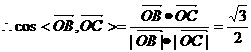 ……6分
……6分
又因为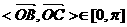
所以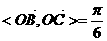 ……7分
……7分
(Ⅱ)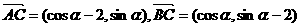
由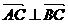 得
得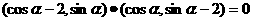 ……9分
……9分
即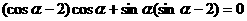
化简得: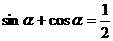 ……10分
……10分
所以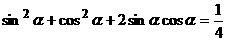
所以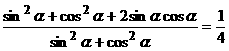
即是
解得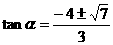 ……12分
……12分
因为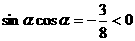
且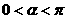
所以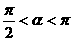 ……13分
……13分
又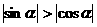
所以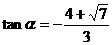 ……14分
……14分
9.四边形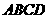 中,
中,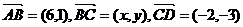
(1)若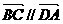 ,试求
,试求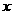 与
与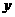 满足的关系式;
满足的关系式;
(2)满足(1)的同时又有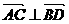 ,求
,求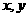 的值及四边形
的值及四边形 的面积。
的面积。
解: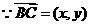 ,
,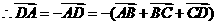
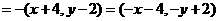 -----------2分
-----------2分
(1)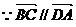 ,故有
,故有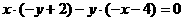 ---------4分
---------4分
化简得: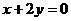 --------------5分
--------------5分
(2)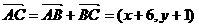
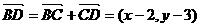
又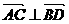 则
则 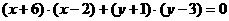 --------7分
--------7分
化简有: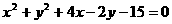 -----------8分
-----------8分
联立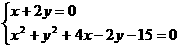
解得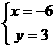 或
或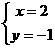 ----------10分
----------10分
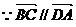
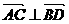 ,则四边形
,则四边形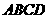 为对角线互相垂直的梯形
为对角线互相垂直的梯形
 当
当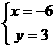
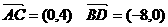
此时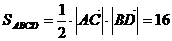 ------12分
------12分
当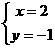
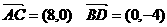
此时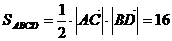 --------------14分
--------------14分
8.已知A、B、C三点的坐标分别为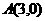 、
、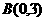 、
、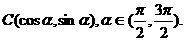
(1)若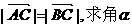 的值; (2)若
的值; (2)若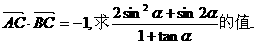
解:(1)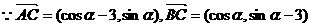 ,
,
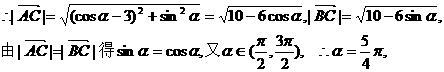
(2)由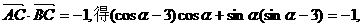
7.广州市海珠区2009届高三上学期综合测试二(数学理)
已知:A、B、C是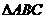 的内角,
的内角,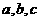 分别是其对边长,向量
分别是其对边长,向量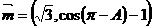 ,
,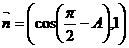 ,
,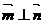 .求角A的大小;
.求角A的大小;
解:(Ⅰ) 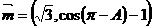 =
= ……1分
……1分
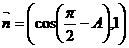 =
=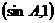 ……2分
……2分
∵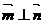
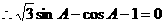 ……4分
……4分
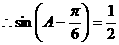 ……6分
……6分
∵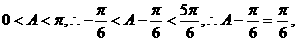 ……7分
……7分
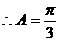 .……8分
.……8分
6. (2008·佛山石门中学检测)在直角坐标系 中,已知点A(0,1)和点B(-3,4),
中,已知点A(0,1)和点B(-3,4),
若点C在∠AOB的一平分线上,且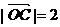 ,则
,则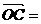 ____________.
____________.
答案: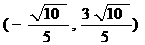 [解析]∵ 点C在
[解析]∵ 点C在
∠AOB的一平分线上,∴ 设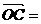
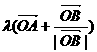 =
=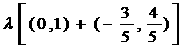
=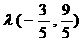
 又
又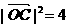 ,∴
,∴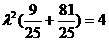 ,得
,得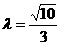 ,
,
∴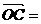
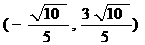
综合拔高训练
5. 一个30º的斜面上放有一个质量为1kg的球,若要保持球在斜面上静止不动,应沿斜面方向给球多大_________力;若表示球的重力的向量为p,球对斜面的压力为ω,则球的重力沿斜面方向的分力f=___________保持球在斜面上静止不动的推力f′=
答案:4.9N, f=p-ω , ,f′=-f=ω-p
4. 在ΔABC中,O为中线AM上的一个动点,若AM=2,则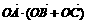 的最小值为
的最小值为
.
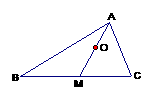 答案:
答案: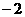 如图,设
如图,设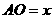 ,则
,则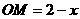 ,
,
所以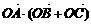
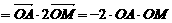
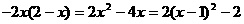 ,
,
故当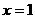 时,
时,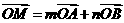 取最小值-2.
取最小值-2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com