
题目列表(包括答案和解析)
5. 如图,设P、Q为△ABC内的两点,且
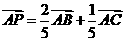 ,
, 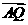 =
=
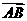 +
+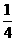
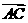 ,则△ABP的面积与△ABQ的面积之比为( )
,则△ABP的面积与△ABQ的面积之比为( )
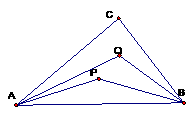 A.
A.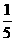 B.
B. 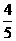 C.
C. 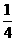 D.
D.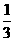
答案:B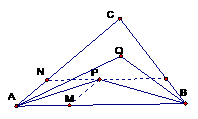 [解析]如图,设
[解析]如图,设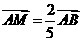 ,
,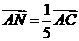 则
则 由平行四边形法则知NP∥AB,所以
由平行四边形法则知NP∥AB,所以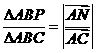 =
=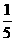 ,同理可得
,同理可得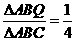 。
。
故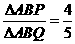 ,即选B.
,即选B.
4.(广东省黄岐高级中学2009届高三月考)
如图,线段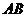 与
与 互相平分,则
互相平分,则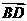 可以表示为 ( )
可以表示为 ( )
A . 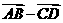 B.
B. 
C. 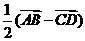 D.
D. 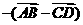
答案:B 线段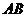 与
与 互相平分,所以
互相平分,所以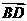 =
=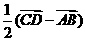
3.已知a=(1,2),b=(-3,2),当ka+b与a-3b平行,k为何值( )
A
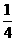 B -
B -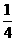 C -
C -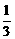 D
D 
答案:C解析: 由已知a=(1,2),b=(-3,2), 得
a-3b=(10,-4), ka+b=(k-3,2k+2).
因(ka+b)∥(a-3b),
故10(2k+2)+4(k-3)=0.
得k=-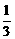 .
.

2. (广东省深圳外国语学校2009届高三统测(数学理))
在 中,
中,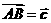 ,
,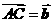 .若点
.若点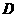 满足
满足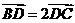 ,则
,则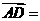 (
)
(
)
A.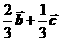 B.
B.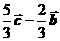 C.
C.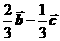 D.
D.
答案:A 解析:由 ,
,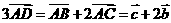 ,
,
1. (广东省惠州市2009届高三第二次调研考试)
设平面向量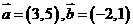 ,则
,则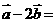 ( )
( )
A.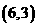 B.
B.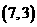 C.
C.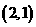 D.
D. 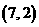
答案:B 解析: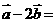
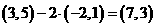
6.已知点O(0,0),A(1,2),B(4,5)及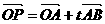 ,
,
求(1)t为何值时,P在x轴上?P在y轴上?P在第二象限。
(2)四边形OABP能否构成为平行四边形?若能,求出相应的t值;若不能,请说明理由。
解:(1) 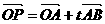 =(1+3t,2+3t),若P在x轴上,只需2+3t=0,∴
=(1+3t,2+3t),若P在x轴上,只需2+3t=0,∴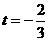 ;若P 在y轴上,只需1+3t=0,∴
;若P 在y轴上,只需1+3t=0,∴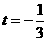 ;若P在第二象限,只需
;若P在第二象限,只需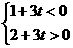 ∴
∴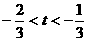
(2)∵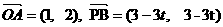 若OABP为平行四边形,
若OABP为平行四边形,
则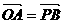
由于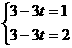 无解,故四边形OABP不能构成平行四边形。
无解,故四边形OABP不能构成平行四边形。
★ 抢 分 频 道 ★
基础巩固训练
5.若向量 =(-1,x)与
=(-1,x)与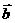 =(-x, 2)共线且方向相同,求x
=(-x, 2)共线且方向相同,求x
解:∵ =(-1,x)与
=(-1,x)与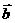 =(-x, 2) 共线 ∴(-1)×2- x•(-x)=0
=(-x, 2) 共线 ∴(-1)×2- x•(-x)=0
∴x=± ∵
∵ 与
与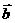 方向相同 ∴x=
方向相同 ∴x=
4.若M(3,
-2) N(-5, -1) 且 
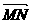 , 求P点的坐标;
, 求P点的坐标;
解:设P(x, y) 则(x-3, y+2)=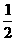 (-8, 1)=(-4,
(-8, 1)=(-4, 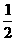 )
)
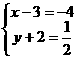 ∴
∴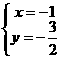 ∴P点坐标为(-1, -
∴P点坐标为(-1, -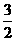 )
)
考点三: 向量平行的充要条件
题型1: 平行、共线问题
[例4] (广东省高明一中2009届高三月考)
已知向量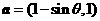 ,
,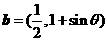 ,若
,若 ∥
∥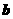 ,则锐角
,则锐角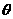 等于( )
等于( )
A.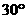 B.
B. 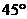 C.
C. D.
D.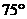
[解题思路]: 已知a、b的坐标,当求a//b时,运用两向量平行的充要条件x1y2-x2y1=0可求 值.
值.
解析:B 解: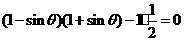 ,故选B
,故选B
[名师指引]数学语言常有多种表达方式,学会转化与变通是求解的关键.本题以几何特征语言形式出现,最终落足点要变式成方程的语言来求解,这一思想方法在求解向量问题时经常用到.
[新题导练]
3. 若A(0, 1), B(1,
2), C(3, 4) 则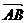 -2
-2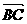 =
=
答案:(-3,-3) 解: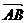 -2
-2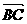 =(1,1)-2(2,2)=(-3,-3)
=(1,1)-2(2,2)=(-3,-3)
2.在△ABC中,已知 AM︰AB =1︰3, AN︰AC =1︰4,BN与CM交于点P,且
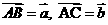 ,试 用
,试 用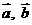 表示
表示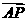 .
.
解:∵ AM︰AB =1︰3, AN︰AC =1︰4,,
∴ 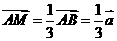 ,
, ,
,
∵ M、P、C三点共线,故可设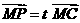 ,t∈R
, 于是,
,t∈R
, 于是,
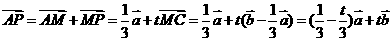 …… ①
…… ①
同理可设设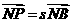 ,s∈R
,
,s∈R
,  .…②
.…②
由①②得 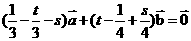 ,
,
由此解得 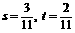 ,∴
,∴  .
.
考点二: 平面向量的坐标表示与运算
题型1: 向量加、减、数乘的坐标运算
[例3] 已知A(-2,4)、B(3,-1)、C(-3,-4)且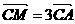 ,
,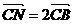 ,求点M、N的坐标及向量
,求点M、N的坐标及向量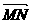 的坐标.
的坐标.
[解题思路]: 利用平面向量的基本本概念及其坐标表示求解。
解析: ∵A(-2,4)、B(3,-1)、C(-3,-4)∴ 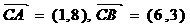
∴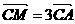 =3(1,8)=(3,24),
=3(1,8)=(3,24),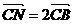 =2(6,3)=(12,6)
=2(6,3)=(12,6)
设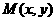 ,则
,则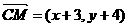
因此  得
得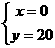 ,∴
,∴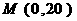
同理可得 ,∴
,∴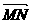 =(9-0,2-20)=(9,-18)
=(9-0,2-20)=(9,-18)
[名师指引]灵活运用向量的坐标运算公式。
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com