
题目列表(包括答案和解析)
4、(2011•潍坊)如图,阴影部分是由5个小正方形涂黑组成的一个直角图形,再将方格内空白的两个小正方形涂黑,得到新的图形(阴影部分),其中不是轴对称图形的是( )

A、 B、
B、
C、 D、
D、
考点:轴对称图形。
分析:本题需先根据轴对称图形的有关概念沿某直线折叠后直线两旁的部分互相重合对每一个图形进行分析即可得出正确答案.
解答:解:A∵沿某直线折叠,分成的两部分能互相重合
∴它是轴对称图形
B、∵沿某直线折叠,分成的两部分能互相重合
∴它是轴对称图形
C、∵绕某一点旋转180°以后,能够与原图形重合
∴它是轴对称图形
D、根据轴对称定义
它不是轴对称图形
故选D.
点评:本题主要考查了轴对称图形的有关概念,在解题时要注意轴对称图形的概念与实际相结合是本题的关键.
3、(2011•潍坊)如图,△ABC中,BC=2,DE是它的中位线,下面三个结论:(1)DE=1;(2)△ADE∽△ABC;(3)△ADE的面积与△ABC的面积之比为1:4.其中正确的有( )
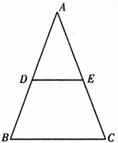
A、0个 B、1个
C、2个 D、3个
考点:相似三角形的判定与性质;三角形中位线定理。
专题:几何综合题。
分析:本题需先根据相似三角形的判定和性质以及三角形的中位线的性质逐个分析,即可得出正确答案.
解答:解:(1)∵△ABC中,BC=2,DE是它的中位线,
∴DE=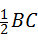
=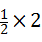
=1
故本选项正确;
(2)∵△ABC中,DE是它的中位线
∴DE∥BC
∴△ADE∽△ABC
故本选项正确;
(3)∵△ADE∽△ABC,相似比为1:2
∴△ADE的面积与△ABC的面积之比为1:4.
故本选项正确
故选D.
点评:本题主要考查了相似三角形的判定和性质,在解题时要注意与三角形的中位线的性质相结合是本题的关键.
2、(2011•潍坊)我国以2010年11月1日零时为标准时点进行了笫六次全国人口普查,普查得到全国总人口为1370536875人,该数用科学记数法表示为( )(保留3个有效数字)
A、13.7亿 B、13.7×108
C、1.37×109 D、1.4×109
考点:科学记数法与有效数字。
分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于1370536875有10位,所以可以确定n=10﹣1=9.
有效数字的计算方法是:从左边第一个不是0的数字起,后面所有的数字都是有效数字.
用科学记数法表示的数的有效数字只与前面的a有关,与10的多少次方无关.
解答:解:1370536875=1.370536875×109≈1.37×109.
故选:C.
点评:此题主要考查了科学记数法的表示方法,以及用科学记数法表示的数的有效数字的确定方法.
1、(2011•潍坊)下面计算正确的是( )
A、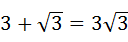 B、
B、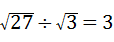
C、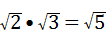 D、
D、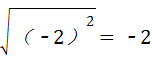
考点:二次根式的混合运算。
专题:计算题。
分析:根据二次根式的混合运算方法,分别进行运算即可.
解答:解:A.3+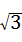 不是同类项无法进行运算,故此选项错误;
不是同类项无法进行运算,故此选项错误;
B.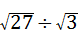 =
=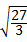 =
=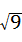 =3,故此选项正确;
=3,故此选项正确;
C.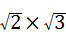 =
=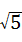 ,
,
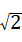 ×
×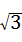 =
=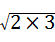 =
=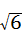 ,故此选项错误;
,故此选项错误;
D.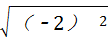 =﹣2,
=﹣2,
∵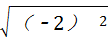 =
=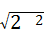 =2,故此选项错误;
=2,故此选项错误;
故选:B.
点评:此题主要考查了二次根式的混合运算,熟练化简二次根式后,在加减的过程中,有同类二次根式的要合并;相乘的时候,被开方数简单的直接让被开方数相乘,再化简;较大的也可先化简,再相乘,灵活对待.
21、(2011•菏泽)如图,抛物线y=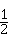 x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A,B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当MC+MD的值最小时,求m的值.
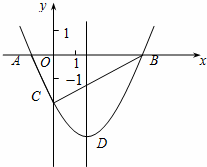
考点:二次函数综合题。
分析:(1)把A点的坐标代入抛物线解析式,求b得值,即可的出抛物线的解析式,根据顶点坐标公式,即可求出顶点坐标;
(2)根据直角三角形的性质,推出AC2=OA2+OC2=5,BC2=OC2+OB2=20,即AC2+BC2=25=AB2,即可确△ABC是直角三角形;
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC'=2.连接C'D交x轴于点M,根据轴对称性及两点之间线段最短可知,MC+MD的值最小.首先确定最小值,然后根据三角形相似的有关性质定理,求m的值
解答:解:(1)把点A(﹣1,0)的坐标代入抛物线的解析式y=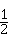 x2+bx﹣2,
x2+bx﹣2,
整理后解得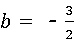 ,
,
所以抛物线的解析式为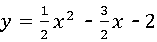 .(2分)
.(2分)
顶点D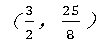 ;(3分)
;(3分)
(2)AB=5.AC2=OA2+OC2=5,BC2=OC2+OB2=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形.(6分)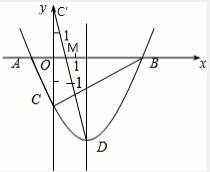
(3)作出点C关于x轴的对称点C′,则C′(0,2),OC′=2.连接C′D交x轴于点M,
根据轴对称性及两点之间线段最短可知,MC+MD的值最小.
设抛物线的对称轴交x轴于点E,
△C′OM∽△DEM.
∴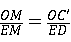 ,
,
∴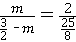 ,
,
∴m=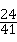 .(10分)
.(10分)
点评:本题着重考查了待定系数法求二次函数解析式、直角三角形的性质及判定、轴对称性质以及相似三角形的性质,关键在于求出函数表达式,做好辅助点,找对相似三角形.
20、(2011•菏泽)我市一家电子计算器专卖店每只进价13元,售价20元,多买优惠;凡是一次买10只以上的,每多买1只,所买的全部计算器每只就降低0.10元,例如,某人买20只计算器,于是每只降价0.10×(20﹣10)=1(元),因此,所买的全部20只计算器都按照每只19元计算,但是最低价为每只16元.
(1)求一次至少买多少只,才能以最低价购买?
(2)写出该专卖店当一次销售x(时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)若店主一次卖的只数在10至50只之间,问一次卖多少只获得的利润最大?其最大利润为多少?
考点:二次函数的应用。
专题:应用题。
分析:(1)设一次购买x只,才能以最低价购买,根据题意列出有关x的一元一次方程,解得即可;
(2)根据购买的数量的不同有不同的优惠方法,故本题时一个分段函数,注意自变量的取值范围;
(3)列出有关购买只数的二次函数求其最大值即可,可以采用配方法求其最值,也可以用公式求其最值.
解答:解:(1)设一次购买x只,才能以最低价购买,
则有:0.1(x﹣10)=20﹣16,
解这个方程得x=50;
答一次至少买50只,才能以最低价购买.
(2)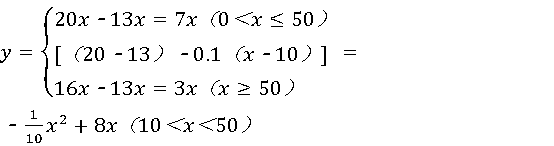 .
.
(3)将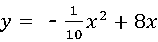
配方得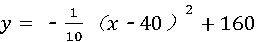 ,
,
∴店主一次卖40只时可获得最高利润,最高利润为160元.
(也可用公式法求得)
点评:本题考查了二次函数的应用,特别是题目中的分段函数,一定要注意自变量的取值范围.
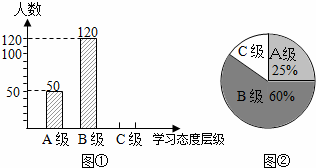
19、(2011•菏泽)初中生对待学习的态度一直是教育工作者关注的问题之一.为此菏泽市教育局对我市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 200 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近80000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
考点:条形统计图;用样本估计总体;扇形统计图。
专题:数形结合。
分析:(1)根据A级的人数与所占的百分数即可求出总人数.
(2)用总人数减去其他两个等级的人数,求出C等级的人数再画图即可解答.
(3)先算出C级在总体中所占的百分数,再算出圆心角的度数,公式是各部分扇形圆心角的度数=部分占总体的百分比×360°.
(4)用样本中学习态度达标的百分数乘以总人数即可解答.
解答:解:(1)50÷25%=200;(2分)
(2)200﹣120﹣50=30(人).画图如下.
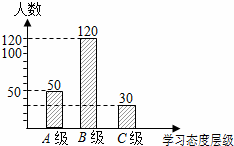 (5分)
(5分)
(3)C所占圆心角度数=360°×(1﹣25%﹣60%)=54°.(8分)
(4)12000×(25%+60%)=10200,
∴估计该市初中生中大约有10200名学生学习态度达标.(10分)
点评:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
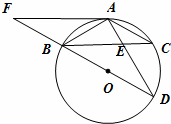
18、(2011•菏泽)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
考点:相似三角形的判定与性质;勾股定理;圆周角定理;切线的判定。
专题:计算题;证明题。
分析:(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.
(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.
(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可.
解答:解:(1)证明:
∵AB=AC,
∴∠ABC=∠C,
∵∠C=∠D,
∴∠ABC=∠D,
又∵∠BAE=∠EAB,
∴△ABE∽△ADB,
(2)∵△ABE∽△ADB,
∴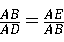 ,
,
∴AB2=AD•AE=(AE+ED)•AE=(2+4)×2=12,
∴AB=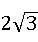 .
.
(3)直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,
∴∠BAD=90°,
∴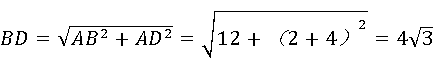 ,
,
BF=BO=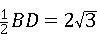 ,
,
∵AB=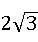 ,
,
∴BF=BO=AB,
∴∠OAF=90°,
∴直线FA与⊙O相切.
点评:此题主要考查相似三角形的判定与性质,勾股定理,圆周角定理,切线的判定等知识点,有一定的拔高难度,属于难题.
17、(2011•菏泽)(1)已知一次函数y=x+2与反比例函数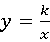 ,其中一次函数y=x+2的图象经过点P(k,5).
,其中一次函数y=x+2的图象经过点P(k,5).
①试确定反比例函数的表达式;
②若点Q是上述一次函数与反比例函数图象在第三象限的交点,求点Q的坐标.
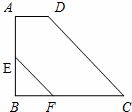
(2)如图,在梯形ABCD中,AD∥BC,∠B=90°,∠C=45°,AD=1,BC=4,E为AB中点,EF∥DC交BC于点F,求EF的长.
考点:反比例函数与一次函数的交点问题;勾股定理;平行四边形的判定与性质;梯形;平行线分线段成比例。
专题:证明题;数形结合;待定系数法。
分析:(1)①由一次函数y=x+2的图象经过点P(k,5)可以得到5=k+2,可以求出k,也就求出了反比例函数的表达式;
②由于点Q是上述一次函数与反比例函数图象在第三象限的交点,联立得方程组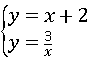 ,解方程组即可求解;
,解方程组即可求解;
(2)过点A作AG∥DC,然后证明四边形AGCD是平行四边形,根据平行四边形的性质得到GC=AD,然后利用已知条件求出BG,再在Rt△ABG中利用勾股定理求出AG,又EF∥DC∥AG,利用平行线分线段成比例即可解决问题.
解答:解:(1)①因一次函数y=x+2的图象经过点P(k,5),
所以得5=k+2,
解得k=3,
所以反比例函数的表达式为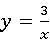 ;(3分)
;(3分)
②联立得方程组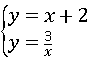 ,
,
解得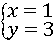 或
或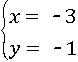 ,
,
故第三象限的交点Q的坐标为(﹣3,﹣1).
(2)解:过点A作AG∥DC,
∵AD∥BC,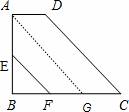
∴四边形AGCD是平行四边形,(2分)
∴GC=AD,
∴BG=BC﹣AD=4﹣1=3,
在Rt△ABG中,
AG=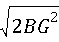 =
=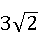 ,(4分)
,(4分)
∵EF∥DC∥AG,
∴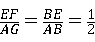 ,
,
∴EF=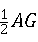 =
=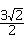 .(6分)
.(6分)
点评:此题的第一小题考查了待定系数法确定函数的解析式和函数图象的交点坐标与解析式的关系,第二小题考查了梯形的性质、勾股定理、平行线分线段成比例的定理即平行四边形的性质与判定,有一定的综合性,难度不大.
16、(2011•菏泽)(1)解方程: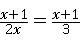
(2)解不等式组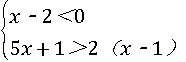 .
.
考点:解分式方程;解一元一次不等式组。
分析:(1)观察方程可得最简公分母是:6x,两边同时乘最简公分母可把分式方程化为整式方程来解答;
(2)先解得两个不等式的解集,再求公共部分.
解答:(1)解:原方程两边同乘以6x,
得3(x+1)=2x•(x+1)
整理得2x2﹣x﹣3=0(3分)
解得x=﹣1或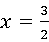
检验:把x=﹣1代入6x=﹣6≠0,
把x=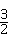 代入6x=9≠0,
代入6x=9≠0,
∴x=﹣1或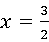 是原方程的解,
是原方程的解,
故原方程的解为x=﹣1或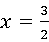 (6分)
(6分)
(若开始两边约去x+1由此得解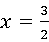 可得3分)
可得3分)
(2)解:解不等式①得x<2(2分)
解不等式②得x>﹣(14分)
∴不等式组的解集为﹣1<x<2(6分)
点评:本题考查了分式方程和不等式组的解法,注:
(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
(3)不等式组的解集的四种解法:大大取大,小小取小,大小小大中间找,大大小小找不到.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com