
题目列表(包括答案和解析)
1. (2011山东滨州,9,3分)在△ABC中,∠C=90°, ∠C=72°,AB=10,则边AC的长约为(精确到0.1)( )
A.9.1 B.9.5 C.3.1 D.3.5
[答案]C
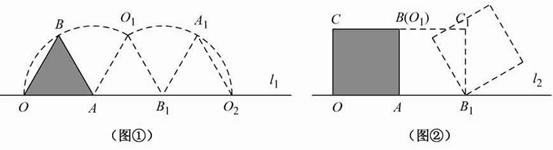
4. (2011江苏苏州,28,9分)(本题满分9分)如图①,小慧同学吧一个正三角形纸片(即△OAB)放在直线l1上,OA边与直线l1重合,然后将三角形纸片绕着顶点A按顺时针方向旋转120°,此时点O运动到了点O1处,点B运动到了点B1处;小慧又将三角形纸片AO1B1绕B1点按顺时针方向旋转120°,点A运动到了点A1处,点O1运动到了点O2处(即顶点O经过上述两次旋转到达O2处).
小慧还发现:三角形纸片在上述两次旋转过程中,顶点O运动所形成的图形是两段圆弧,即弧OO1和弧O1O2,顶点O所经过的路程是这两段圆弧的长度之和,并且这两端圆弧与直线l1围成的图形面积等于扇形AOO1的面积、△AO1B1的面积和扇形B1O1O2的面积之和.
小慧进行类比研究:如图②,她把边长为1的正方形纸片OABC放在直线l2上,OA边与直线l2重合,然后将正方形纸片绕着顶点A按顺时针方向旋转90°,此时点O运动到了点O1处(即点B处),点C运动到了点C1处,点B运动到了点B1处;小慧又将正方形纸片AO1C1B1绕B1点按顺时针方向旋转90°,……,按上述方法经过若干次旋转后,她提出了如下问题:
问题①:若正方形纸片OABC按上述方法经过3次旋转,求顶点O经过的路程,并求顶点O在此运动过程中所形成的图形与直线l2围成图形的面积;若正方形OABC按上述方法经过5次旋转,求顶点O经过的路程;
问题②:正方形纸片OABC按上述方法经过多少次旋转,顶点O经过的路程是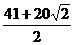 π?
π?
请你解答上述两个问题.
[答案]解问题①:如图,正方形纸片OABC经过3次旋转,顶点O运动所形成的图形是三段弧,即弧OO1、弧O1O2以及弧O2O3,
∴顶点O运动过程中经过的路程为
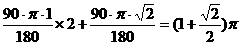 .
.
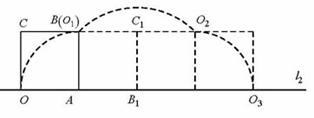
顶点O在此运动过程中所形成的图形与直线l2围成图形的面积为
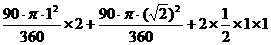 =1+π.
=1+π.
正方形OABC经过5次旋转,顶点O经过的路程为
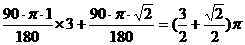 .
.
问题②:∵方形OABC经过4次旋转,顶点O经过的路程为
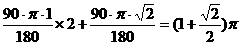
∴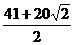 π=20×
π=20×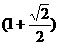 π+
π+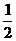 π.
π.
∴正方形纸片OABC经过了81次旋转.
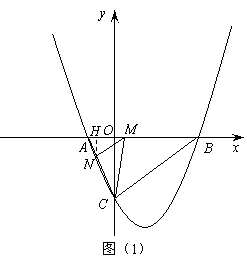
3. (2011四川凉山州,28,12分)如图,抛物线与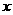 轴交于
轴交于 (
(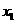 ,0)、
,0)、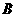 (
( ,0)两点,且
,0)两点,且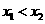 ,与
,与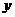 轴交于点
轴交于点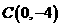 ,其中
,其中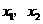 是方程
是方程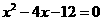 的两个根。
的两个根。
(1)求抛物线的解析式;
(2)点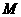 是线段
是线段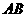 上的一个动点,过点
上的一个动点,过点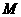 作
作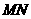 ∥
∥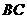 ,交
,交 于点
于点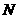 ,连接
,连接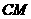 ,当
,当 的面积最大时,求点
的面积最大时,求点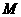 的坐标;
的坐标;
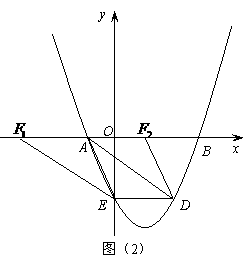
(3)点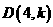 在(1)中抛物线上,点
在(1)中抛物线上,点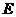 为抛物线上一动点,在
为抛物线上一动点,在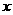 轴上是否存在点
轴上是否存在点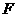 ,使以
,使以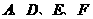 为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点
为顶点的四边形是平行四边形,如果存在,求出所有满足条件的点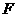 的坐标,若不存在,请说明理由。
的坐标,若不存在,请说明理由。
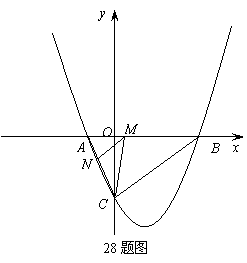

[答案]
(1)∵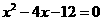 ,∴
,∴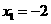 ,
,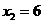 。
。
∴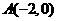 ,
,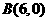 。
。
又∵抛物线过点 、
、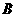 、
、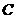 ,故设抛物线的解析式为
,故设抛物线的解析式为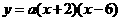 ,将点
,将点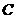 的坐标代入,求得
的坐标代入,求得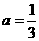 。
。
∴抛物线的解析式为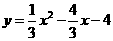 。
。
(2)设点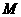 的坐标为(
的坐标为( ,0),过点
,0),过点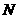 作
作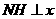 轴于点
轴于点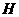 (如图(1))。
(如图(1))。
∵点 的坐标为(
的坐标为(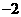 ,0),点
,0),点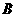 的坐标为(6,0),
的坐标为(6,0),
∴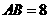 ,
,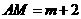 。
。
∵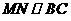 ,∴
,∴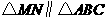 。
。
∴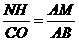 ,∴
,∴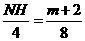 ,∴
,∴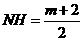 。
。
∴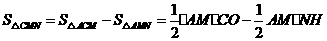

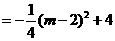 。
。
∴当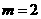 时,
时, 有最大值4。
有最大值4。
此时,点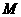 的坐标为(2,0)。
的坐标为(2,0)。
(3)∵点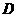 (4,
(4,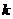 )在抛物线
)在抛物线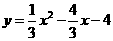 上,
上,
∴当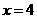 时,
时,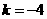 ,
,
∴点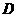 的坐标是(4,
的坐标是(4,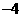 )。
)。
①
如图(2),当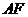 为平行四边形的边时,
为平行四边形的边时,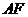


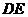 ,
,
∵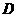 (4,
(4,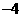 ),∴错误!链接无效。
),∴错误!链接无效。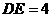 。
。
∴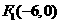 ,
,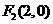 。
。
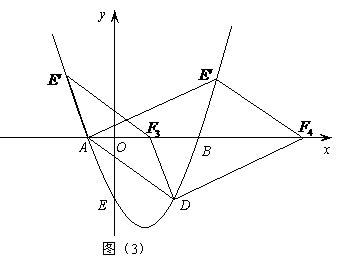
②
如图(3),当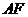 为平行四边形的对角线时,设
为平行四边形的对角线时,设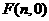 ,
,
则平行四边形的对称中心为(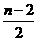 ,0)。
,0)。
∴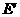 的坐标为(
的坐标为(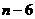 ,4)。
,4)。
把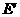 (
(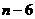 ,4)代入
,4)代入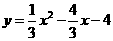 ,得
,得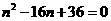 。
。
解得 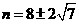 。
。
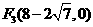 ,
,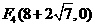 。
。
2. (2011江苏南通,27,12分)(本小题满分12分)
已知A(1,0), B(0,-1),C(-1,2),D(2,-1),E(4,2)五个点,抛物线y=a (x-1)2+k(a>0),经过其中三个点.
(1) 求证:C,E两点不可能同时在抛物线y=a (x-1)2+k(a>0)上;
(2) 点A在抛物线y=a (x-1)2+k(a>0)上吗?为什么?
(3) 求a和k的 值.
[答案](1)证明:将C,E两点的坐标代入y=a (x-1)2+k(a>0)得,
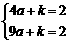 ,解得a=0,这与条件a>0不符,
,解得a=0,这与条件a>0不符,
∴C,E两点不可能同时在抛物线y=a (x-1)2+k(a>0)上.
(2)[法一]∵A、C、D三点共线(如下图),
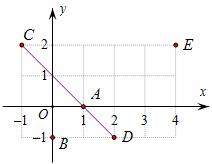
∴A、C、D三点也不可能同时在抛物线y=a (x-1)2+k(a>0)上.
∴同时在抛物线上的三点有如下六种可能:
①A、B、C;
②A、B、E;
③A、B、D;
④A、D、E;
⑤B、C、D;
⑥B、D、E.
将①、②、③、④四种情况(都含A点)的三点坐标分别代入y=a (x-1)2+k(a>0),解得:①无解;②无解;③a=-1,与条件不符,舍去;④无解.
所以A点不可能在抛物线y=a (x-1)2+k(a>0)上.
[法二]∵抛物线y=a (x-1)2+k(a>0)的顶点为(1,k)
假设抛物线过A(1,0),则点A必为抛物线y=a (x-1)2+k(a>0)的顶点,由于抛物线的开口向上且必过五点A、B、C、D、E中的三点,所以必过x轴上方的另外两点C、E,这与(1)矛盾,所以A点不可能在抛物线y=a (x-1)2+k(a>0)上.
(3)Ⅰ.当抛物线经过(2)中⑤B、C、D三点时,则
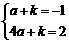 ,解得
,解得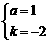
Ⅱ. 当抛物线经过(2)中⑥B、D、E三点时,同法可求: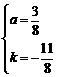 .
.
∴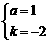 或
或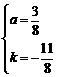 .
.
1. (2011江苏南京,28,11分)
问题情境
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
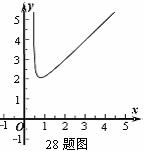
设该矩形的长为x,周长为y,则y与x的函数关系式为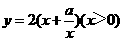 .
.
探索研究
⑴我们可以借鉴以前研究函数的经验,先探索函数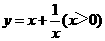 的图象性质.
的图象性质.
① 填写下表,画出函数的图象:
|
x |
…… |
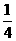 |
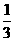 |
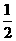 |
1 |
2 |
3 |
4 |
…… |
|
y |
…… |
|
|
|
|
|
|
|
…… |
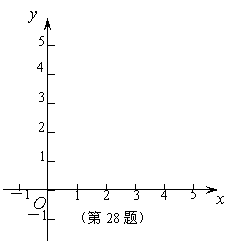
②观察图象,写出该函数两条不同类型的性质;
③在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.请你通过配方求函数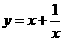 (x>0)的最小值.
(x>0)的最小值.
解决问题
⑵用上述方法解决“问题情境”中的问题,直接写出答案.
[答案]解:⑴①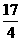 ,
,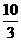 ,
,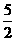 ,2,
,2,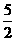 ,
,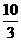 ,
,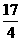 .
.
函数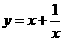
 的图象如图.
的图象如图.
②本题答案不唯一,下列解法供参考.
当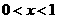 时,
时,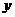 随
随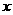 增大而减小;当
增大而减小;当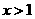 时,
时,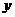 随
随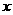 增大而增大;当
增大而增大;当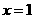 时函数
时函数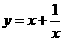
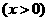 的最小值为2.
的最小值为2.
③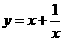
=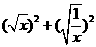
=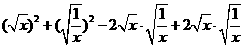
=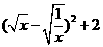
当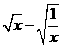 =0,即
=0,即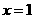 时,函数
时,函数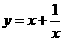
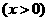 的最小值为2.
的最小值为2.
⑵当该矩形的长为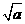 时,它的周长最小,最小值为
时,它的周长最小,最小值为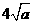 .
.
41. (2011湖北荆州,19,7分)(本题满分7分)如图,P是矩形ABCD下方一点,将△PCD绕P点顺时针旋转60°后恰好D点与A点重合,得到△PEA,连接EB,问△ABE是什么特殊三角形?请说明理由.
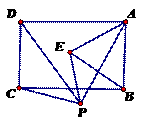
[答案]△ABE是等边三角形,理由如下:
因为△PEA是将△PCD绕P点顺时针旋转60°后得到的
所以△PEA≌△PCD,且AE与DC所夹的锐角为60°
所以AE=DC
又因为四边形ABCD是矩形
所以DC=AB且DC∥AB
所以AE=AB且∠EAB=60°
所以△ABE是等边三角形.
40. (2011湖南湘潭市,24,8分)(本题满分8分)
两个全等的直角三角形重叠放在直线 上,如图⑴,AB=6cm,BC=8cm,
上,如图⑴,AB=6cm,BC=8cm,
∠ABC=90°,将Rt△ABC在直线 上左右平移,如图⑵所示.
上左右平移,如图⑵所示.
⑴ 求证:四边形ACFD是平行四边形;
⑵ 怎样移动Rt△ABC,使得四边形ACFD为菱形;
⑶ 将Rt△ABC向左平移 ,求四边形DHCF的面积.
,求四边形DHCF的面积.
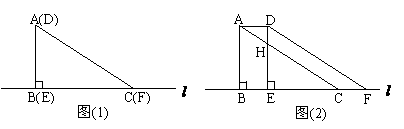

[答案] (1)证明:∵△ABC≌△DEF,∴AC=DF,∠ACB=∠DFE,∴AC∥DF,
∴四边形ACFD是平行四边形;
(2)在Rt△ABC中,由勾股定理得AC=10cm,要使四边形ACFD为菱形,则AC=CF,
∴可将Rt△ABC向左平移10cm或向右平移10cm;
(3)在Rt△ABC中,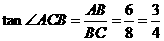 .
.
∴当Rt△ABC向左平移 时,EC=BC-BE=8-4=4(cm),
时,EC=BC-BE=8-4=4(cm),
在Rt△HEC中,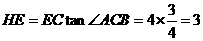 .
.
∴四边形DHCF的面积为: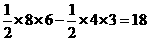 cm2.
cm2.
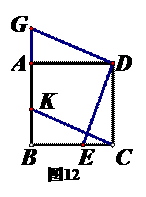
39. (2011河北,23,9分)如图12,四边形ABCD是正方形,点E,K分别在BC,AB上,点G在BA的延长线上,且CE=BK=AG.
(1)求证:①DE=EG;
②DE⊥EG;
(2)尺规作图:以线段DE,DG为边作出正方形DEFG(要求:只保留作图痕迹,不写作法和证明);
(3)连接(2)中的KF,猜想并写出四边形CEFK是怎样的特殊四边形,并证明你的猜想;
(4)当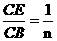 时,请直接写出
时,请直接写出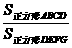 的值.
的值.
[答案](1)证明:∵四边形ABCD是正方形,∴DC=DA,∠DCE=∠DAG=90°,又∵CE=AG,∴△DCE≌△DAG,∴∠EDC=∠GDA,DE=DG.又∵∠ADE+∠EDC=90°,∴∠ADE+∠GDA=90°,∴DE⊥DG.
(2)如图
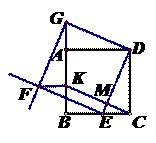
(3)四边形CEFK为平行四边形。
证明:设CK,DE相交于M点,∵四边形ABCD和四边形DEFG都是正方形,∴AB∥CD,AB=CD,EF=DG,EF∥DG;∵BK=AG,∴KG=AB=CD,∴四边形CKGD为平行四边形。∴CK=DG=EF,CK∥DG.∴∠KME=∠GDE=∠DEF=90°.∴∠KME+∠DEF=180°,∴CK∥EF,∴四边形CKEF为平行四边形。
(4)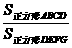 =
=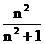
38. (2011贵州安顺,25,10分)如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.
⑴说明四边形ACEF是平行四边形;
⑵当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.
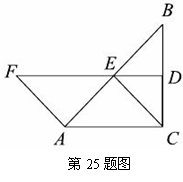

[答案](1)证明:由题意知∠FDC =∠DCA = 90°.∴EF∥CA ∴∠AEF =∠EAC
∵AF = CE = AE ∴∠F =∠AEF =∠EAC =∠ECA 又∵AE = EA
∴△AEC≌△EAF,∴EF = CA,∴四边形ACEF是平行四边形 .
(2)当∠B=30°时,四边形ACEF是菱形 .
理由是:∵∠B=30°,∠ACB=90°,∴AC=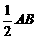 ,∵DE垂直平分BC,∴ BE=CE
,∵DE垂直平分BC,∴ BE=CE
又∵AE=CE,∴CE=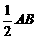 ,∴AC=CE,∴四边形ACEF是菱形.
,∴AC=CE,∴四边形ACEF是菱形.
37. (20011江苏镇江,25,6分)已知:如图1,图形①满足:AD=AB,MD=MB, ∠A=72°, ∠M=144°.图形②与图形①恰好拼成一个菱形(如图2).记作AB的长度为a,BM的长度为b.
(1)图中①中∠B=___度,图中②中∠E=____度.
(2)小明有两种纸片各若干张,其中一种纸片的形状及大小与图形①相同,这咱纸片称为“风筝一号”另一种纸片的形状及大小与图形②相同,这种纸片称为“飞镖一号”.
①小明仅有“,风筝一号”纸片拼成一个边长为b的正十边形,需要这种纸片____张;
②小明用若干张“风筝一号”和 “飞镖一号”纸片拼成一个“大风筝”(如图3),其中
∠P=72°, ∠Q=144°,PI=PJ=a+b,IQ=JQ.庄股你在图穷匕见中画出拼接线并保留画图痕迹.(本题中均为无重叠、无缝隙拼接)
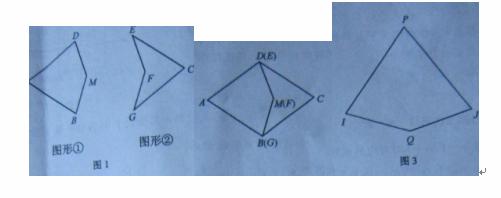
[答案](1)∠B=72°,∠E=36°
(2)5个;
(3)图略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com