
题目列表(包括答案和解析)
8.点P到A(1,0)和直线x=-1的距离相等,且点P到直线l:y=x的距离等于,则这样的点P的个数为________.
解析:由抛物线定义,知点P的轨迹为抛物线,其方程为y2=4x,设点P的坐标为,由点到直线的距离公式,知=,即y-4y0±4=0,易知y0有三个解,故点P个数有三个.
答案:3
7.已知抛物线型拱的顶点距离水面2米时,测量水面宽为8米,当水面上升米后,水面的宽度是________.
解析:设抛物线方程为x2=-2py,将(4,-2)代入方程得16=-2p·(-2),解得2p=8,
故方程为x2=-8y,水面上升米,则y=-,代入方程,得x2=-8×=12,x=±2.故水面宽4米.
答案:4米
6.设抛物线y2=2x的焦点为F,过点M(,0)的直线与抛物线相交于A,B两点,与抛物线的准线相交于点C,|BF|=2,则△BCF与△ACF的面积之比等于( )
A. B.
C. D.
解析:由|BF|=2小于点M到准线的距离知点B在A、C之间,由抛物线的定义知点B的横坐标为,代入得y2=3,则B,另一种可能是,那么此时直线AC的方程为=,即y=,把y=代入y2=2x,可得2x2-7x+6=0,可得x=2,则有y=2,即A(2,2),那么S△BCF?S△ACF=|BC|?|AC|=?=4?5,故选A.
答案:A
5.设F为抛物线y2=4x的焦点,A、B、C为该抛物线上三点,若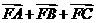 =0,则
=0,则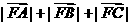 等于( )
等于( )
A.9 B.6
C.4 D.3
解析:设A、B、C三点的坐标分别为(x1,y1),(x2,y2),(x3,y3),F(1,0).
∵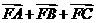 =0,∴x1+x2+x3=3.
=0,∴x1+x2+x3=3.
又由抛物线定义知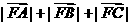 =x1+1+x2+1+x3+1=6,故选B.
=x1+1+x2+1+x3+1=6,故选B.
答案:B
4.若抛物线y2=4x的焦点是F,准线是l,则经过点F、M(4,4)且与l相切的圆共有( )
A.0个 B.1个
C.2个 D.4个
解析:经过F、M的圆的圆心在线段FM的垂直平分线上,设圆心为C,则|CF|=|CM|,又圆C与l相切,所以C到l距离等于|CF|,从而C在抛物线y2=4x上.
故圆心为FM的垂直平分线与抛物线的交点,显然有两个交点,所以共有两个圆,故选C.
答案:C
3.抛物线y2=4x的焦点为F,准线为l,经过F且斜率为的直线与抛物线在x轴上方的部分相交于点A,AK⊥l,垂足为K,则△AKF的面积是( )
A.4 B.3
C.4 D.8
解析:抛物线y2=4x的焦点为F(1,0),准线为l:x=-1,经过F且斜率为的直线y=(x-1)与抛物线在x轴上方的部分相交于点A(3,2),AK⊥l,垂足为K(-1,2),∴△AKF的面积是4.故选C.
答案:C
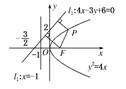
2.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2 B.3
C. D.
解析:如图所示,动点P到l2:x=-1的距离可转化为P到F的距离,由图可知,距离和的最小值即F到直线l1的距离d==2,故选A.
答案:A
1.设斜率为2的直线l过抛物线y2=ax(a≠0)的焦点F,且和y轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( )
A.y2=±4 B.y2=±8x
C.y2=4x D.y2=8x
解析:y2=ax的焦点坐标为.过焦点且斜率为2的直线方程为y=2,令x=0得:y=-.
∴×·=4,
∴a2=64,
∴a=±8,故选B.
答案:B
13.在右图所示的几何体中,平面PAC⊥平面ABC,PM∥BC,PA=PC,AC=1,BC=2PM=2,AB=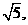 若该几何体的侧视图(左视图)的面积为
若该几何体的侧视图(左视图)的面积为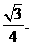
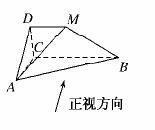
(1)求证:PA⊥BC;
(2)画出该几何体的正视图,并求其面积S;
(3)求出多面体A-BMPC的体积V.
解:(1)证明:AC=1,BC=2,AB=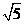 ,
,
∴AC2+BC2=AB2.
∴AC⊥BC.又∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴BC⊥平面PAC.又∵PA⊂平面PAC,∴PA⊥BC.
(2)设几何体的正视图如图所示:
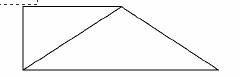
∵PA=PC,取AC的中点D,连接PD,则PD⊥AC.
又平面PAC⊥平面ABC,
∴PD⊥平面ABC.
∴几何体侧视图的面积=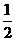 AC·PD
AC·PD
=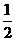 ×1×PD=
×1×PD=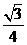 .
.
∴PD=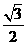 .易知△PAC是边长为1的正三角形.
.易知△PAC是边长为1的正三角形.
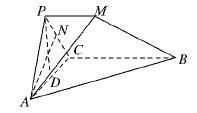
∴正视图的面积是上、下底边长分别为1和2,PD的长为高的直角梯形的面积.
∴S=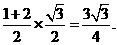
(3)取PC的中点N,连接AN,由△PAC是边长为1的正三角形,可知AN⊥PC,由(1)知BC⊥平面PAC,
∴AN⊥BC,∴AN⊥平面PCBM.
∴AN是四棱锥A-PCBM的高,且AN=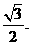
由BC⊥平面PAC,可知BC⊥PC.
由PM∥BC,可知四边形PCBM是上、下底边长分别为1和2,PC的长1为高的直角梯形.
其面积S′=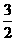 ,∴V=
,∴V=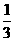 S′·AN=
S′·AN=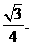
12.如图,在三角形ABC中,若AC=3,BC=4,AB=5,以AB所在直线为轴,将此三角形旋转一周,求所得旋转体的表面积和体积.
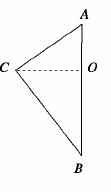
解:如图所示,所得旋转体是两个底面重合的圆锥,高的和为AB=5.底面半径等于CO=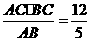 ,所以所得旋转体的表面积S=π·OC·(AC+BC)=π·
,所以所得旋转体的表面积S=π·OC·(AC+BC)=π·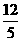 ·(3+4)=
·(3+4)=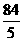 π;其体积V=
π;其体积V=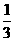 ·π·OC2·AO+
·π·OC2·AO+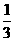 ·π·OC2·BO=
·π·OC2·BO=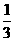 ·π·OC2·AB=
·π·OC2·AB=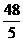 π.
π.
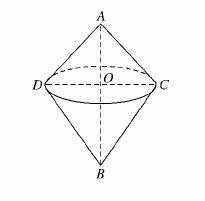
评析:求一些组合体的表面积和体积时,首先要弄清楚它由哪些基本几何体构成,再通过轴截面分析和解决问题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com