
题目列表(包括答案和解析)
1.若已知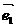 、
、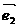 是平面上的一组基底,则下列各组向量中不能作为基底的一组是 ( )
是平面上的一组基底,则下列各组向量中不能作为基底的一组是 ( )
A.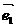 与-
与-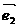 B.3
B.3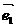 与2
与2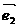 C.
C.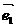 +
+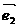 与
与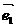 -
-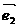 D.
D.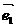 与2
与2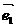
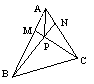 答案:D
答案:D
3.重难点:
(1)平行的情况有方向相同和方向相反两种
问题1:和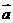 = (3,-4)平行的单位向量是_________;
= (3,-4)平行的单位向量是_________;
错解:因为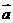 的模等于5,所以与
的模等于5,所以与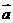 平行的单位向量就是
平行的单位向量就是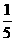
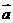 ,即 (,-)
,即 (,-)
错因:在求解平行向量时没有考虑到方向相反的情况。
正解:因为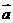 的模等于5,所以与
的模等于5,所以与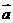 平行的单位向量是
平行的单位向量是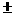
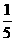
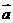 ,即(,-)或(-,)
,即(,-)或(-,)
★ 热 点 考 点 题 型 探 析★
考点一: 平面向量基本定理
题型1. 利用一组基底表示平面内的任一向量
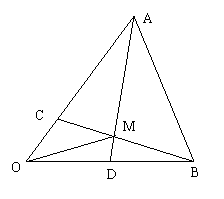
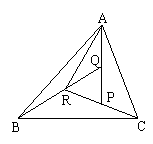
[例1] 在△OAB中,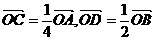 ,AD与BC交于点M,设
,AD与BC交于点M,设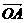 =
=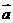 ,
,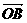 =
=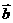 ,用
,用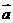 ,
,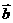 表示
表示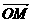 .
.
[解题思路]:若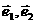 是一个平面内的两个不共线向量,则根据平面向量的基本定理,平面内的任何向量都可用
是一个平面内的两个不共线向量,则根据平面向量的基本定理,平面内的任何向量都可用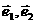 线性表示.本例中向量
线性表示.本例中向量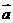 ,
,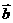 可作基底,故可设
可作基底,故可设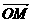 =m
=m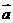 +n
+n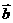 ,为求实数m,n,需利用向量
,为求实数m,n,需利用向量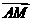 与
与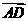 共线,向量
共线,向量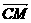 与
与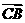 共线,建立关于m,n的两个方程.
共线,建立关于m,n的两个方程.
解析:设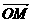 =m
=m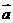 +n
+n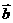 ,
,
则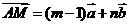 ,
,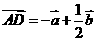
∵点A、M、D共线,∴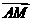 与
与
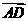 共线,
共线,
∴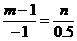 ,∴m+2n=1. ①
,∴m+2n=1. ①
而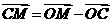
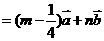 ,
,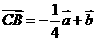
∵C、M、B共线,∴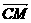 与
与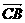 共线,
共线,
 ∴
∴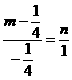 ,∴4m+n=1. ②
,∴4m+n=1. ②
联立①②解得:m=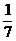 ,n=
,n=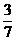 ,∴
,∴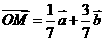
[例2] 已知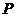 是
是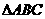 所在平面内一点,
所在平面内一点,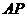 的中点为
的中点为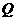 ,
,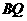 的中点为
的中点为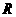 ,
, 的中点为
的中点为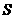 .证明:只有唯一的一点
.证明:只有唯一的一点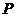 使得
使得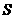 与
与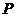 重合.
重合.
[解题思路]:要证满足条件的点是唯一的,只需证明向量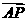 可用一组基底唯一表示.
可用一组基底唯一表示.
解析: [证明]设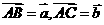 ,
,
则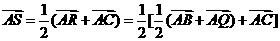
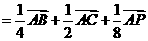 ,
,
由题设知: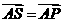
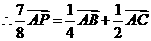
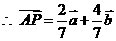
由于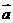 ,
,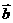 是确定的向量,所以
是确定的向量,所以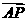 是唯一的一个向量,即
是唯一的一个向量,即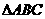 所在平面内只有唯一的一点
所在平面内只有唯一的一点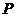 使得
使得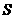 与
与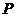 重合.
重合.
[名师指引]解决此类类问题的关键在于以一组不共线的向量主基底,通过向量的加、减、数乘以及向量平行的充要条件,把其它相关的向量用这一组基底表示出来,再利用向量相等建立方程,从而解出相应的值。
[新题导练]
2.难点:用坐标表示的平面向量共线的条件,能用向量的坐标形式判断两向量以及三点是否共线.
1.重点:
(1)了解平面向量基本定理及其意义,了解基底和两个非零向量夹角的概念,会进行向量的分解及正交分解;
(2)理解平面向量的坐标的概念,掌握平面向量的坐标运算,会用坐标表示平面向量的加、减与数乘运算;
4.向量平行的充要条件的坐标表示:设 =(x1, y1) ,
=(x1, y1) ,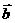 =(x2, y2) 其中
=(x2, y2) 其中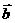 ¹
¹
 ∥
∥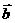 (
(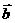 ¹
¹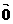 )的充要条件是
)的充要条件是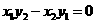
★ 重 难 点 突 破 ★
3.平面向量的坐标运算
(1) 若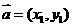 ,
,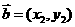 ,则
,则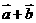 =
=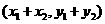 ,
,
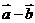 =
= 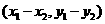
两个向量和与差的坐标分别等于这两个向量相应坐标的和与差
(2) 若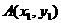 ,
,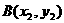 ,则
,则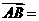
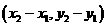
一个向量的坐标等于表示此向量的有向线段的终点坐标减去始点的坐标
(3)若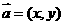 和实数
和实数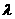 ,则
,则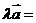
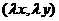
实数与向量的积的坐标等于用这个实数乘原来向量的相应坐标
2.平面向量的坐标表示
如图,在直角坐标系内,我们分别取与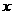 轴、
轴、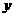 轴方向相同的两个__单位向量_
轴方向相同的两个__单位向量_ 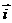 、
、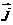 作为基底
作为基底 任作一个向量
任作一个向量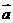 ,由平面向量基本定理知,有且只有一对实数
,由平面向量基本定理知,有且只有一对实数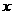 、
、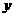 ,使得
,使得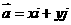 …………1,
…………1,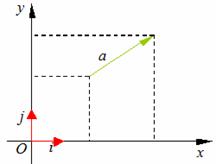
我们把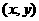 叫做向量
叫做向量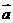 的(直角)坐标,记作
的(直角)坐标,记作
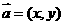 …………2
…………2
其中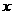 叫做
叫做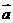 在
在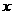 轴上的坐标,
轴上的坐标,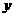 叫做
叫做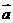 在
在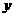 轴上的坐标,2式叫做向量的坐标表示
轴上的坐标,2式叫做向量的坐标表示
与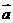 相等的向量的坐标也为
相等的向量的坐标也为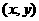

特别地,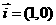 ,
,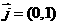 ,
,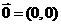

特别提醒:设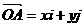 ,则向量
,则向量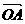 的坐标
的坐标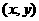 就是点
就是点 的坐标;反过来,点
的坐标;反过来,点 的坐标
的坐标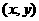 也就是向量
也就是向量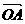 的坐标
的坐标 因此,在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示
因此,在平面直角坐标系内,每一个平面向量都是可以用一对实数唯一表示
1.平面向量基本定理:如果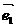 ,
,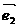 是同一平面内的两个_____不共线_____不共线向量,那么对于这一平面内的__任一__向量
是同一平面内的两个_____不共线_____不共线向量,那么对于这一平面内的__任一__向量 ,有且只有_一对实数λ1,λ2使
,有且只有_一对实数λ1,λ2使 =λ1
=λ1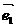 +λ2
+λ2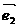
特别提醒:
(1)我们把不共线向量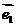 、
、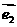 叫做表示这一平面内所有向量的一组基底;
叫做表示这一平面内所有向量的一组基底;
(2)基底不惟一,关键是不共线;
(3)由定理可将任一向量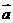 在给出基底
在给出基底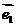 、
、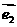 的条件下进行分解;
的条件下进行分解;
(4)基底给定时,分解形式惟一 λ1,λ2是被
λ1,λ2是被 ,
,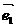 ,
,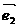 唯一确定的数量
唯一确定的数量
10.广东省恩城中学2009届高三上学期中段考试(数学理)
在△ABC中,已知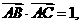
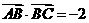 .
.
(1) 求AB边的长度;
(2) 证明:
证明: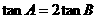 ;
;
(3)若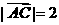 ,求
,求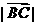 .
.
解:(1)∵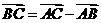 ∴
∴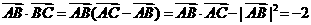
∵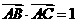 ∴
∴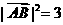 ,
, 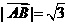 即AB边的长度为
即AB边的长度为 ----------------4分
----------------4分
(2) 由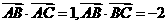 得
得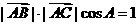 --------------------①
--------------------①
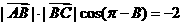 即
即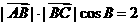 --------------------②-----6分
--------------------②-----6分
 由①②得
由①②得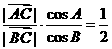 , 由正弦定理得
, 由正弦定理得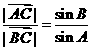
∴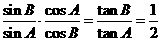
∴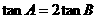 -----------------------------------------------9分
-----------------------------------------------9分
(3) ∵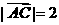 ,由(2)中①得
,由(2)中①得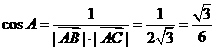
由余弦定理得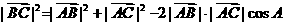 =
=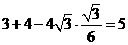
∴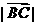 =
=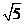 --------------------------------------------------------------------------14分
--------------------------------------------------------------------------14分
9.(广东省五校2009届高三上学期第二次联考(数学理))
设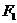 、
、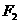 分别是椭圆
分别是椭圆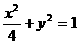 的左、右焦点.若
的左、右焦点.若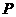 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
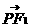 ·
·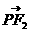 的最大值和最小值;
的最大值和最小值;
解:(Ⅰ)解法一:易知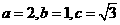 ,所以
,所以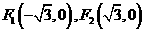
,设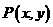 ,则
,则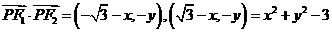
因为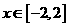 ,故当
,故当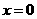 ,即点
,即点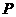 为椭圆短轴端点时,
为椭圆短轴端点时,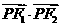 有最小值
有最小值
当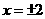 ,即点
,即点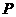 为椭圆长轴端点时,
为椭圆长轴端点时,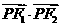 有最大值
有最大值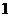
解法二:易知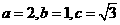 ,所以
,所以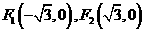
设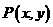 ,则
,则
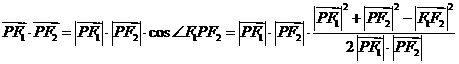
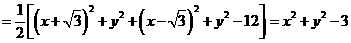 …
…
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com