
题目列表(包括答案和解析)
3. (2008·广东省实验中学高三第三次阶段考)在△ABC中,已知向量
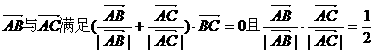 ,则△ABC为( )
,则△ABC为( )
A.三边均不相等的三角形 B.直角三角形
C.等腰非等边三角形 D.等边三角形
答案: D [解析]非零向量与满足(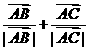 )·=0,即角A的平分线垂直于BC,∴ AB=AC,又
)·=0,即角A的平分线垂直于BC,∴ AB=AC,又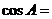
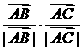 = ,∠A=
= ,∠A=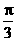 ,所以△ABC为等边三角形
,所以△ABC为等边三角形
2. 已知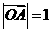 ,
,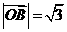 ,
,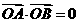 ,点C在
,点C在 内,且
内,且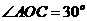 ,设
,设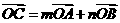
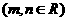 ,则
,则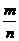 等于 ( )
等于 ( )
A.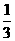 B.3 C.
B.3 C.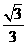 D.
D.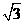
答案B∵ 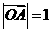 ,
,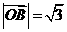 ,
,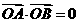
∴△ABC为直角三角形,其中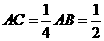
∴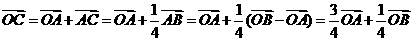
∴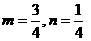 即
即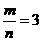 故本题的答案为B.
故本题的答案为B.
1. 如果一架向东飞行200km,再向南飞行300km,记飞机飞行的路程为s,位移为a,则 ( )
A. s>|a| B. s<|a| C. s=|a| D. s与|a|不能比大小
答案:A
6.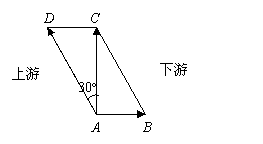 在静水中划船的速度是每分钟40,水流的速度是每分钟20,如果船从岸边出发,径直沿垂直与水流的航线到达对岸,那么船行进的方向应该指向何处?
在静水中划船的速度是每分钟40,水流的速度是每分钟20,如果船从岸边出发,径直沿垂直与水流的航线到达对岸,那么船行进的方向应该指向何处?
答案:船航行的方向是与河岸垂直方向
成30°夹角,即指向河的上游.
★ 抢 分 频 道 ★
基础巩固训练
5.点P在平面上作匀速直线运动,速度向量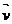 =(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|
=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|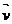 |个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为( )
|个单位.设开始时点P的坐标为(-10,10),则5秒后点P的坐标为( )
A.(-2,4) B (10,-5) C (-30,25) D (5,-10)
答案:B 解析:5秒后点P的坐标为(-10,10)+5(4,-3)= (10,- 5)
4.广东省揭阳二中2009届高三统测(数学理)
在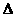 ABC中,a,b,c分别为角A、B、C的对边;若向量
ABC中,a,b,c分别为角A、B、C的对边;若向量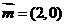 与
与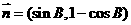 的夹角为
的夹角为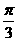 ,求角B的大小
,求角B的大小
解:由题意得: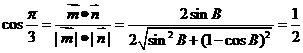 ,即
,即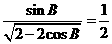
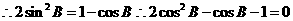
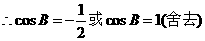
 0<B<
0<B<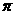
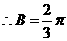 ………6分
………6分
考点三: 平面向量在物理中的应用
题型1: 用向量解决物理问题
[例4] 设炮弹被以初速v0和仰角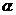 抛出(空气阻力忽略不计).当初速度v0的大小一定时,发射角
抛出(空气阻力忽略不计).当初速度v0的大小一定时,发射角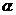 多大时,炮弹飞行的距离最远.
多大时,炮弹飞行的距离最远.
[解题思路]:上述问题中涉及速度等物理量,可根据平面向量的基本定理和物理问题的需要,把v0分解为水平方向和竖直方向两个不共线的向量,再利用运动学知识建立数学模型,最后利用向量的知识求解.
解析:将v0分解为水平方向和竖直方向两个分速度v1和v2,则| v1|=|
v0|cos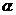 ,
,
|
v2|=| v0|sin 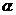 , 由物理学知识可知,
, 由物理学知识可知,
炮弹在水平方向飞行的距离S =| v1|·t=|
v0|cos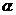 ·t(t是飞行时间) ①
·t(t是飞行时间) ①
炮弹在垂直方向的位移是0=| v2|·t-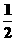 gt2(g是重力加速度) ②
gt2(g是重力加速度) ②
由②得t=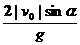 ,③代入①得
,③代入①得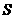 =
=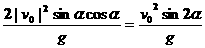
由于| v0|一定,所以当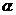 =45°时,S有最大值.
=45°时,S有最大值.
故发射角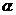 =45°时,炮弹飞行的距离最远.
=45°时,炮弹飞行的距离最远.
[例5] 某人骑车以每小时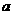 公里的速度向东行驶,感到风从正东方向吹来,而当速度为2
公里的速度向东行驶,感到风从正东方向吹来,而当速度为2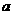 时,感到风从东北方向吹来,试求实际风速和方向.
时,感到风从东北方向吹来,试求实际风速和方向.
[解题思路]:利用向量知识解决物理中有关“速度的合成与分解”
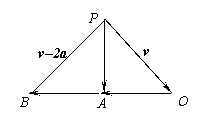
解析: 设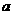 表示此人以每小时a公里的速度向东行驶的向量,
表示此人以每小时a公里的速度向东行驶的向量,
无风时此人感到风速为-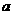 ,设实际风速为v,
,设实际风速为v,
那么此时人感到的风速为v - 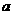 ,设
,设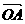 = -
= -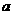 ,
,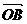 = -2
= -2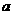
∵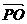 +
+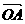 =
=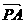 ∴
∴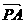 = v -
= v - 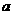 ,
,
这就是感到由正北方向吹来的风速,
∵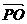 +
+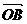 =
=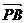 ∴
∴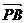 = v -2
= v -2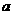 ,于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是
,于是当此人的速度是原来的2倍时所感受到由东北方向吹来的风速就是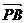 ,由题意:ÐPBO = 45°, PA^BO, BA = AO
,由题意:ÐPBO = 45°, PA^BO, BA = AO
从而,△POB为等腰直角三角形,∴PO = PB =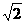
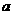 即:|v | =
即:|v | =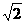
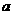
∴实际风速是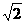
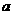 的西北风
的西北风
[名师指引]加强数学应用意识,提高分析问题,解决问题的能力
[新题导练]
3.  广东省高明一中2009届高三月考(数学理)
广东省高明一中2009届高三月考(数学理)
已知向量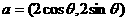 ,
,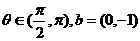 ,则向量
,则向量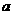 与
与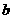 的夹角为( )
的夹角为( )
A.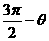 B.
B.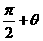 C.
C.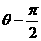 D.
D.
答案:A 解析: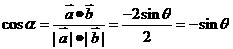 又
又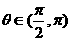 所以选A
所以选A
2.已知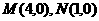 ,若动点
,若动点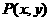 满足
满足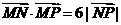 ,求动点P的轨迹方程.
,求动点P的轨迹方程.
[解析] 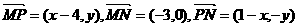
由已知得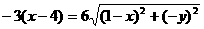 ,
,
化简得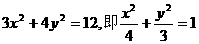 ,这就是动点P的轨迹方程.
,这就是动点P的轨迹方程.
考点二: 平面向量与三角函数、函数等知识的综合应有用
题型1: 与函数综合题
[例2] 广东省华南师大附中2009届高三综合测试(数学理)
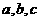 为△
为△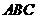 的内角A、B、C的对边,
的内角A、B、C的对边,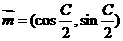 ,
,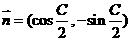 ,且
,且 与
与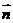 的夹角为
的夹角为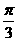 ,求C;
,求C;
[解题思路]: 考查向量数量积运算及三角函数二倍角公式
解析: ∵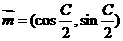 ,
,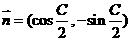
∴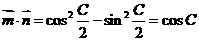
又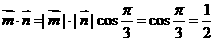
∴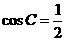 ,∴
,∴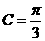
[例3] 广东省揭阳二中2009届高三统测(数学理)
已知A、B、C是直线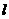 上的不同的三点,O是外一点,向量
上的不同的三点,O是外一点,向量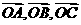 满足
满足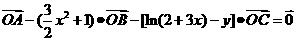 ,记
,记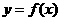 .求函数
.求函数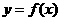 的解析式;
的解析式;
[解题思路]: A、B、C三点共线,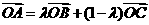
解析: 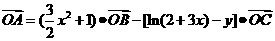
 A、B、C三点共线,
A、B、C三点共线,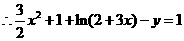
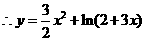 ………3分
………3分
[名师指引]涉及与三角综合的题目,多数只利用向量的基本运算,把问题转化为三角问题,以考查三角函数知识为主。三点共线是一个常考常新的知识点。要记住常用结论:A、B、C三点共线,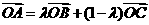
[新题导练]
1.证明:三角形重心与顶点的距离等于它到对边中点的距离的两倍.
[解析] 设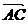 = b,
= b,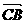 = a,则
= a,则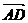 =
=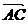 +
+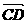 = b+
= b+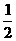 a,
a, 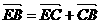 =
=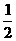 b+a
b+a
∵A, G, D共线,B, G, E共线
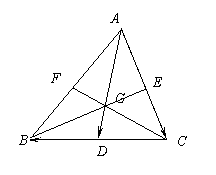 ∴可设
∴可设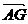 =λ
=λ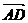 ,
,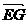 = μ
= μ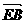 ,
,
则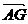 =λ
=λ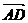 =λ(b+
=λ(b+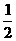 a)=λb+
a)=λb+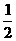 λa,
λa,
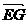 = μ
= μ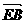 = μ(
= μ(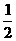 b+ a)=
b+ a)=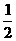 μb+μa,
μb+μa,
∵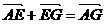 即:
即: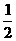 b + (
b + (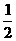 μb+μa) =λb+
μb+μa) =λb+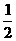 λa
λa
∴(μ-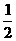 λ) a + (
λ) a + (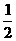 μ-λ+
μ-λ+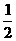 )b = 0 ∵a, b不平行,
)b = 0 ∵a, b不平行,
∴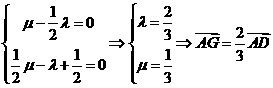
3.重难点:.
1 熟悉向量的性质及运算律;
熟悉向量的性质及运算律;
2 能根据向量性质特点构造向量;
能根据向量性质特点构造向量;
3 熟练平面几何性质在解题中应用;
熟练平面几何性质在解题中应用;
4 熟练向量求解的坐标化思路
熟练向量求解的坐标化思路
5 认识事物之间的内在联系;
认识事物之间的内在联系;
6 认识向量的工具性作用,加强数学在实际生活中的应用意识
认识向量的工具性作用,加强数学在实际生活中的应用意识
★ 热 点 考 点 题 型 探 析★
 考点一:平面向量在平面几何
考点一:平面向量在平面几何
题型1. 用向量证明几何题
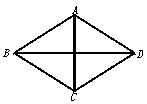
[例1] 已知:如图所示,ABCD是菱形,AC和BD是它的两条对角线 求证AC⊥BD
求证AC⊥BD
[解题思路]:对于线段的垂直,可以联想到两个向量垂直的充要条件,而对于这一条件的应用,可以考虑向量式的形式,也可以考虑坐标形式的充要条件
解析:证法一:∵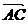 =
=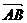 +
+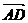 ,
,
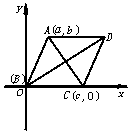
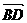 =
=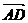 -
-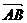 ,
,
∴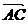 ·
·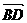 =(
=(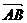 +
+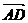 )·(
)·(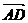 -
-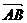 )
)
=|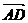 |2-|
|2-|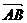 |2=O
|2=O
∴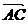 ⊥
⊥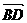
证法二:以OC所在直线为x轴,以B为原点建立直角坐标系,设B(O,O),A(a,b),C(c,O)则由|AB|=|BC|得a2+b2=c2
∵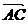 =
=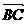 -
-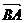 =(c,O)-(a,b)=(c-a,-b),
=(c,O)-(a,b)=(c-a,-b),
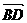 =
=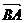 +
+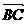 =(a,b)+(c,O)=(c+a,b)
=(a,b)+(c,O)=(c+a,b)
∴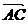 ·
·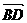 =c2-a2-b2=O
=c2-a2-b2=O
∴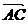 ⊥
⊥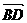 即 AC⊥BD
即 AC⊥BD
[名师指引]如能熟练应用向量的坐标表示及运算,则将给解题带来一定的方便 通过向量的坐标表示,可以把几何问题的证明转化成代数式的运算,体现了向量的数与形的桥梁作用。
通过向量的坐标表示,可以把几何问题的证明转化成代数式的运算,体现了向量的数与形的桥梁作用。
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com