
题目列表(包括答案和解析)
11.一个正三棱柱的三视图如图所示,求这个三棱柱的表面积和体积.
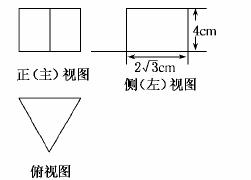
分析:由几何体的三视图,画出原几何体的直观图,然后求解即可.
解:由三视图易知,该正三棱柱的形状如图所示.
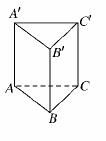
可知AA′=BB′=CC′=4 cm,正三角形ABC和正三角形A′B′C′的高为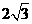 cm,
cm,
∴正三角形ABC的边长为|AB|=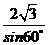 =4(cm),
=4(cm),
∴该三棱柱的表面积为S=3×4×4+2×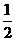 ×42sin60°=(48+8
×42sin60°=(48+8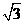 )(cm2),体积为V=S底•|AA′|=
)(cm2),体积为V=S底•|AA′|=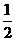 ×42sin60°×4=16
×42sin60°×4=16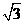 (cm3).
(cm3).
故这个三棱柱的表面积为(48+8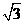 )cm2,体积为16
)cm2,体积为16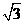 cm3.
cm3.
评析:(1)注意:侧(左)视图中的数据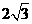 cm为底面正三角形的高,不要误认为是正三角形的边长.(2)通过三视图间接给出几何体的形状,打破以往直接给出几何体,并给出相关数据进行相关运算的传统模式,使三视图与传统意义上的几何有机结合,这也体现了新课标的思想,应是高考的新动向,希望引起大家注意.
cm为底面正三角形的高,不要误认为是正三角形的边长.(2)通过三视图间接给出几何体的形状,打破以往直接给出几何体,并给出相关数据进行相关运算的传统模式,使三视图与传统意义上的几何有机结合,这也体现了新课标的思想,应是高考的新动向,希望引起大家注意.
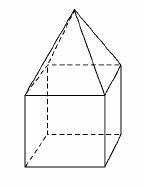
10.已知一个凸多面体共有9个面,所有棱长均为1,其平面展开图如图所示,则该凸多面体的体积V=________.
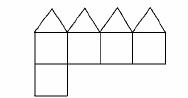
解析:该几何体形状如图所示,是一个正方体与正四棱锥的组合体,正方体的体积是1,正四棱锥的体积是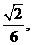 故该凸多面体的体积为
故该凸多面体的体积为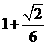 .
.
答案: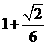
三、解答题:(本大题共3小题,11、12题13分,13题14分,写出证明过程或推演步骤.)
9.(2010·广州模拟)如图为一几何体的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及点P,D,C,R共线,沿图中虚线将它们折叠起来,使P,Q,R,S四点重合,则需要________个这样的几何体,可以拼成一个棱长为6的正方体.
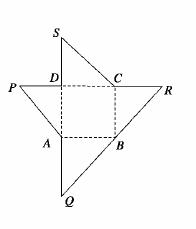
解析:由题意知,将该展开图沿虚线折叠起来以后,得到一个四棱锥P-ABCD(如图),其中PD⊥平面ABCD,因此该四棱锥的体积V=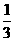 ×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要
×6×6×6=72,而棱长为6的正方体的体积V=6×6×6=216,故需要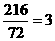 个这样的几何体,才能拼成一个棱长为6的正方体.
个这样的几何体,才能拼成一个棱长为6的正方体.
答案:3
评析:几何体的展开与折叠问题是近几年高考的一个热点内容,通过折叠与展开问题,可以很好地考查学生的空间想象能力以及推理能力.解决折叠与展开问题时,关键是弄清楚折叠与展开前后,位置关系和数量关系变化的情况,画出准确的图形解决问题.
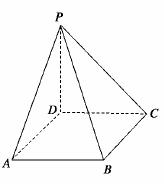
8.(2010·烟台检测)已知三棱柱ABC-A1B1C1的体积为V,E是棱CC1上一点,三棱锥E-ABC的体积是V1,则三棱锥E-A1B1C1的体积是________.
解析:如图,过E作AC、BC的平行线EF、EG,分别与AA1、BB1交于F、G,连接FG.
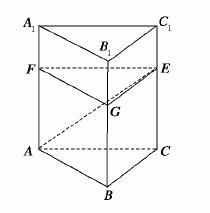
∵三棱锥E-ABC的体积是V1,∴三棱柱EFG-CAB的体积是3V1,
∴三棱柱EFG-C1A1B1的体积是V-3V1,
∵VE-A1B1C1=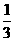 VEFG-C1A1B1,
VEFG-C1A1B1,
∴VE-A1B1C1=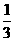 (V-3V1)=
(V-3V1)=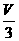 -V1.
-V1.
答案: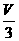 -V1
-V1
7.已知某个几何体的三视图如图(正视图中的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是________cm3.
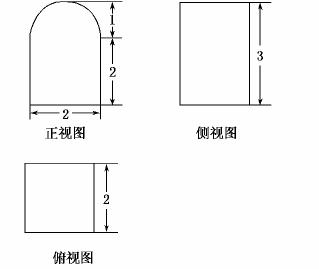
解析:该几何体由半个圆柱和一个正方体构成的组合体.
其体积为23+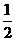 ×π×2=(8+π) cm3.
×π×2=(8+π) cm3.
答案:8+π
6.(原创题)设计一个杯子,其三视图如图所示,现在向杯中匀速注水,杯中水面的高度h随时间t变化的图象是( )
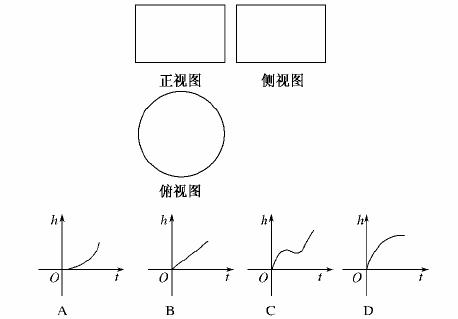
解析:由三视图可知杯子是圆柱形的,由于圆柱形的杯子上下大小相同,所以当向杯中匀速注水时,其高度随时间的变化是相同的,反映在图象上,选项B符合题意.故选B.
答案:B
二、填空题:(本大题共4小题,每小题6分,共24分,把正确答案填在题后的横线上.)
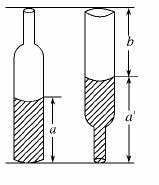
5.如图,啤酒瓶的高为h,瓶内酒面高度为a,若将瓶盖盖好倒置,酒面高度为a′(a′+b=h),则酒瓶容积与瓶内酒的体积之比为( )
A.1+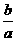 且a+b>h
且a+b>h
B.1+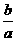 且a+b<h
且a+b<h
C.1+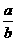 且a+b>h
且a+b>h
D.1+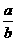 且a+b<h
且a+b<h
解析:设酒瓶下底面面积为S,则酒的体积为Sa,酒瓶的体积为Sa+Sb,故体积之比为1+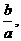 显然有a<a′,又a′+b=h,故a+b<h.选B.
显然有a<a′,又a′+b=h,故a+b<h.选B.
答案:B
4.如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为( )
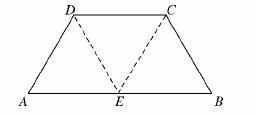
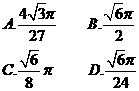
解析:由已知条件知,平面图形中AE=EB=BC=CD=DA=DE=EC=1.
∴折叠后得到一个正四面体.
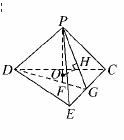
作PF⊥平面DEC,垂足为F,F即为△DEC的中点.
取EC中点G,连接DG、PG,
过球心O作OH⊥平面PEC.
则垂足H为△PEC的中心.
∵PG=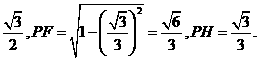
∴OP=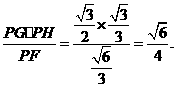
∴外接球体积为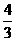 π×OP3=
π×OP3=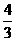 ×π×
×π×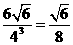 π.
π.
答案:C
3.已知几何体的三视图如图所示,它的表面积是( )
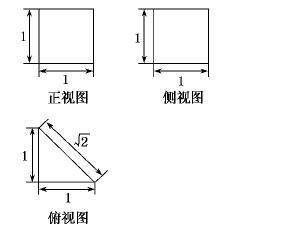
解析:该几何体为直三棱柱,其表面积为2×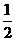 ×1×1+2×12+
×1×1+2×12+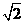 ×1=3+
×1=3+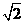 ,选C.
,选C.
答案:C
2.如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为( )
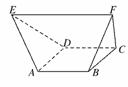
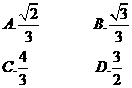
解析:如图,将几何体割成一个三棱柱和两个相同的三棱锥.
在梯形ABFE中,易知BN=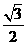 ,
,
∴S△BCN=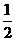 BC·HN=
BC·HN= ×1×
×1×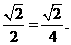
故该几何体体积为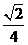 ×1+2×
×1+2×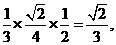 选A.
选A.
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com