
题目列表(包括答案和解析)
14、(2011•潍坊)一个y关于x的函数同时满足两个条件:①图象过(2,1)点;②当x>0时,y随x的增大而减小.这个函数解析式为 如:y=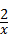 ,y=﹣x+3,y=﹣x2+5等 .(写出一个即可)
,y=﹣x+3,y=﹣x2+5等 .(写出一个即可)
考点:二次函数的性质;一次函数的性质;反比例函数的性质。
专题:开放型。
分析:本题的函数没有指定是什么具体的函数,可以从一次函数,反比例函数,二次函数三方面考虑,只要符合条件①②即可.
解答:解:符合题意的函数解析式可以是y=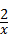 ,y=﹣x+3,y=﹣x2+5等,(本题答案不唯一)
,y=﹣x+3,y=﹣x2+5等,(本题答案不唯一)
故答案为:y=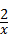 ,y=﹣x+3,y=﹣x2+5等.
,y=﹣x+3,y=﹣x2+5等.
点评:本题考查了一次函数,反比例函数,二次函数的性质.关键是从三种函数解析式上考虑,只要符合题意即可.
13、(2011•潍坊)分解因式:a3+a2﹣a﹣1= (a﹣1)(a+1)2.
考点:因式分解-分组分解法。
专题:因式分解。
分析:当被分解的式子是四项时,应考虑运用分组分解法进行分解.本题应采用两两分组,然后提取公因式a+1,注意分解要彻底.
解答:解:a3+a2﹣a﹣1=(a3+a2)﹣(a+1)=a2(a+1)﹣(a+1)=(a+1)(a2﹣1)=(a+1)(a+1)(a﹣1)=(a﹣1)(a+1)2.
故答案为:(a﹣1)(a+1)2.
点评:本题考查了分组分解法分解因式,难点是采用两两分组还是三一分组.注意分解要彻底.
12、(2011•潍坊)已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1,x2满足x1+x2=4和x1•x2=3,那么二次函数ax2+bx+c(a>0)的图象有可能是( )
A、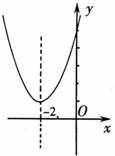 B、
B、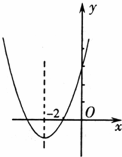
C、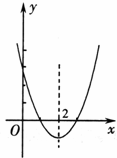 D、
D、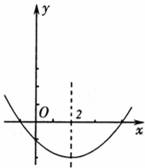
考点:抛物线与x轴的交点;二次函数的图象。
专题:数形结合。
分析:根据二次函数二次函数y=ax2+bx+c(a>0)的图象与x轴的交点横坐标就是一元二次方程ax2+bx+c=0(a>0)的两个实数根,利用两个实数根x1,x2满足x1+x2=4和x1•x2=3,求得两个实数根,作出判断即可.
解答:解:∵已知一元二次方程ax2+bx+c=0(a>0)的两个实数根x1,x2满足x1+x2=4和x1•x2=3,
∴x1,x2是一元二次方程x2﹣4x+3=0的两个根,
解得:x1=1,x2=3
∴二次函数ax2+bx+c(a>0)与x轴的交点坐标为(1,0)和(3,0)
故选C.
点评:本题考查了抛物线与x轴的交点坐标及二次函数的图象,解题的关键是根据题目提供的条件求出抛物线与横轴的交点坐标.
11、(2011•潍坊)已知直角梯形ABCD中,AD∥BC,∠BCD=90°,BC=CD=2AD,E、F分别是BC、CD边的中点,连接BF、DE交于点P,连接CP并延长交AB于点Q,连接AF.则下列结论不正确的是( )
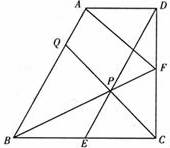
A、CP平分∠BCD B、四边形ABED为平行四边形
C、CQ将直角梯形分为面积相等的两部分 D、△ABF为等腰三角形
考点:直角梯形;全等三角形的判定与性质;平行四边形的判定与性质。
专题:证明题;几何综合题。
分析:本题可用排除法证明,即证明A、B、D正确,C不正确;易证△BCF≌△DCE(SAS),得∠FBC=∠EDC,∴△BPE≌△DPF,∴BP=DP;∴△BPC≌△DPC,∴∠BCP=∠DCP,∴A正确;∵AD=BE且AB∥BE,所以,四边形ABED为平行四边形,B正确;∵BF=ED,AB=ED,∴AB=BF,即D正确;
解答:证明:易证△BCF≌△DCE(SAS),
∴∠FBC=∠EDC,BF=ED;
∴△BPE≌△DPF(AAS),
∴BP=DP,
∴△BPC≌△DPC(SSS),
∴∠BCP=∠DCP,即A正确;
又∵AD=BE且AB∥BE,
∴四边形ABED为平行四边形,B正确;
∵BF=ED,AB=ED,
∴AB=BF,即D正确;
综上,选项A、B、D正确;
故选C.

点评:本题考查了等腰三角形、平行四边形和全等三角形的判定,熟记以上图形的性质,并能灵活运用其性质,是解答本题的关键,本题综合性较好.
10、(2011•潍坊)身高相等的四名同学甲、乙、丙、丁参加风筝比赛,四人放出风筝的线长、线与地面的夹角如下表(假设风筝线是拉直的),则四名同学所放的风筝中最高的是( )
|
同学 |
甲 |
乙 |
丙 |
丁 |
|
放出风筝线长 |
140m |
100m |
95m |
90m |
|
线与地面夹角 |
30° |
45° |
45° |
60° |
A、甲 B、乙
C、丙 D、丁
考点:解直角三角形的应用-坡度坡角问题。
专题:计算题。
分析:根据题意画出图形,分别利用解直角三角形的知识求出风筝的高再进行比较即可.
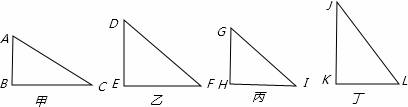
解答:解:如图,
甲中,AC=140m,∠C=30°,AB=140×sin30°=70m;
乙中,DF=100m,∠C=45°,DE=100×sin45°=50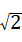 ≈70.71m;
≈70.71m;
丙中,GI=95m,∠I=45°,GH=95×sin45°=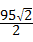 ≈67.18m;
≈67.18m;
丁中,JK=90m,∠C=60°,AB=90×sin60°=45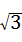 ≈77.9m.
≈77.9m.
可见JK最大,故选D.
点评:此题考查了解直角三角形的应用﹣﹣﹣坡度坡角问题,画出图形,直接根据解直角三角形的知识解答即可,要熟悉特殊角的三角函数值.
9、(2011•潍坊)如图,半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,则小圆扫过的阴影部分的面积为( )
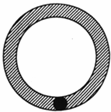
A、17π B、32π
C、49π D、80π
考点:圆与圆的位置关系。
专题:几何图形问题。
分析:由半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,即可求得空白处的圆的半径,即可求得阴影部分的面积.
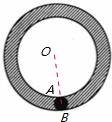
解答:解:∵半径为1的小圆在半径为9的大圆内滚动,且始终与大圆相切,
∴OB=9,AB=2,
∴OA=7,
∴小圆扫过的阴影部分的面积为:81π﹣49π=32π.
故选B.
点评:此题考查了圆与圆的位置关系.注意求得空白处的圆的半径是解此题的关键.
8、(2011•潍坊)在今年我市初中学业水平考试体育学科的女子800米耐力测试中,某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,下列说法正确的是( )
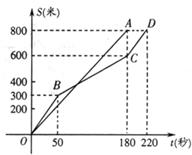
A、小莹的速度随时间的增大而增大 B、小梅的平均速度比小莹的平均速度大
C、在起跑后180秒时,两人相遇 D、在起跑后50秒时,小梅在小莹的前面
考点:函数的图象。
专题:数形结合。
分析:A、由于线段OA表示所跑的路程S(米)与所用时间t(秒)之间的函数图象,由此可以确定小莹的速度是没有变化的,
B、小莹比小梅先到,由此可以确定小梅的平均速度比小莹的平均速度是否小;
C、根据图象可以知道起跑后180秒时,两人的路程确定是否相遇;
D、根据图象知道起跑后50秒时OB在OA的上面,由此可以确定小梅是否在小莹的前面.
解答:解:A、∵线段OA表示所跑的路程S(米)与所用时间t(秒)之间的函数图象,∴小莹的速度是没有变化的,故选项错误;
B、∵小莹比小梅先到,∴小梅的平均速度比小莹的平均速度小,故选项错误;
C、∵起跑后180秒时,两人的路程不相等,∴他们没有相遇,故选项错误;
D、∵起跑后50秒时OB在OA的上面,∴小梅是在小莹的前面,故选项正确.
故选D.
点评:本题考查利用函数的图象解决实际问题,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
7、(2011•潍坊)关于x的方程x2+2kx+k﹣1=0的根的情况描述正确的是( )
A、k为任何实数,方程都没有实数根 B、k为任何实数,方程都有两个不相等的实数拫
C、k为任何实数,方程都有两个相等的实数根 D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种
考点:根的判别式。
分析:本题需先求出方程的根的判别式的值,然后得出判别式大于0,从而得出答案.
解答:解:∵关于x的方程x2+2kx+k﹣1=0中
△=(2k)2﹣4×(k﹣1)
=4k2﹣4k+4
=(2k﹣1)2+3>0
∴k为任何实数,方程都有两个不相等的实数根
故选B.
点评:本题主要考查了根的判别式的概念,在解题时要能对根的判别式进行整理变形是本题的关键.
6、(2011•潍坊)某市2011年5月1日﹣10日十天的空气污染指数的数据如下(主要污染物为可吸入颗粒物):
61,75,70,56,81,91,92,91,75,81.
那么该组数据的极差和中位数分别是( )
A、36,78 B、36,86
C、20,78 D、20,77.3
考点:极差;中位数。
专题:计算题。
分析:求极差的方法是用一组数据中的最大值减去最小值;中位数是把数据从小到大排列起来,位置处于最中间的数就是中位数.
解答:解:极差:92﹣56=36,
将这组数据从小到大的顺序排列56,61,70,75,75,81,81,91,91,92,
处于中间位置的那个数,75和81,所以中位数是(75+81)÷2=78.
故选:A.
点评:此题主要考查了极差,中位数的求法,准确把握这两种数的概念是做题的关键.
5、(2011•潍坊)不等式组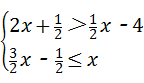 的解集在数轴上表示正确的是( )
的解集在数轴上表示正确的是( )
A、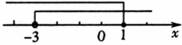 B、
B、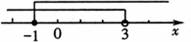
C、 D、
D、
考点:在数轴上表示不等式的解集;解一元一次不等式组。
专题:存在型。
分析:先分别求出各不等式的解集,并在数轴上表示出来,再找出符合条件的选项即可.
解答:解: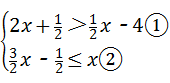 ,由①得,x>﹣3,由②得,x≤1,
,由①得,x>﹣3,由②得,x≤1,
故原不等式组的解集为:﹣3<x≤1,
在数轴上表示为:

故选A.
点评:本题考查的是在数轴上表示一元一次不等式组的解集,在解答此类问题时要注意实心圆点与空心圆点的区别.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com