
题目列表(包括答案和解析)
9.已知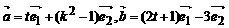 ,且
,且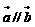 ,试求t关于k的函数。
,试求t关于k的函数。
答案: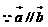 ,则 -3t = ( 2t + 1 )( k2 –
1 )
,则 -3t = ( 2t + 1 )( k2 –
1 )

8.已知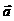 +
+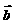 =
=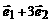 ,
,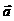 -
-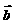 =
= ,用
,用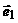 、
、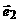 表示
表示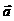 = 。
= 。
答案: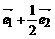 提示:(
提示:(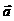 +
+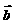 )+(
)+(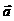 -
-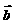 )=
)=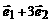 +
+ =
=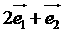
所以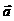 =
=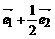
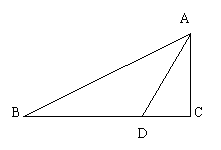
7.(安徽省合肥市2008年高三年级第一次质检)如图,已知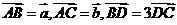 ,用
,用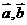 表示
表示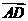 ,则
,则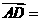 ( )
( )
A.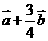 B.
B.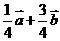 C.
C.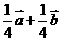 D.
D.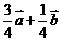
答案:B
解析: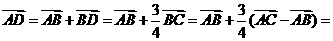
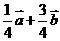
6.(广东北江中学2008高三统测)
若 则向量
则向量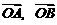 的关系是( )
的关系是( )
A.平行 B.重合 C.垂直 D.不确定
 答案:C 提示:
答案:C 提示: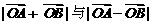 分别表示平行四边形的两条对角线,它们相等,即说明四边形ABCD为矩形。故选C
分别表示平行四边形的两条对角线,它们相等,即说明四边形ABCD为矩形。故选C
综合拔高训练
5.已知: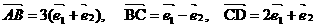 ,则下列关系一定成立的是( )
,则下列关系一定成立的是( )
A、A,B,C三点共线 B、A,B,D三点共线
C、C,A,D三点共线 D、B,C,D三点共线
答案:C 解析: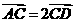 ,所以C,A,D三点共线
,所以C,A,D三点共线
4..D、E、F分别是△ABC的BC、CA、AB上的中点,且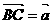 ,
, 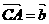 ,给出下列命题,其中正确命题的个数是( )
,给出下列命题,其中正确命题的个数是( )
①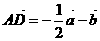 ②
②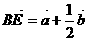
③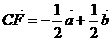 ④
④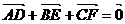
A、1 B、2 C、3 D、4
答案:D 提示:结合图形及向量加减法的几何意义,易得4个命题均是正确命题。
3.已知向量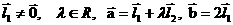 ,若向量
,若向量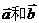 共线,则下列关系一定成立的是( )
共线,则下列关系一定成立的是( )
A、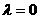 B、
B、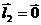 C、
C、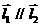 D、
D、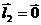 或
或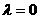
答案:D 提示:考虑情况要充分。
2. (四川省成都市一诊)在四边形ABCD中,“”是“四边形ABCD为梯形”的
A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件
答案:A 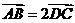 Þ 四边形ABCD为梯形,但反之不成立.选A
Þ 四边形ABCD为梯形,但反之不成立.选A
1. 判断下列命题是否正确,并说明理由:
(1)共线向量一定在同一条直线上。 ( )
(2)所有的单位向量都相等。 ( )
(3)向量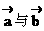 共线,
共线,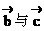 共线,则
共线,则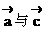 共线。 ( )
共线。 ( )
(4)向量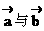 共线,则
共线,则 ( )
( )
(5)向量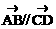 ,则
,则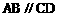 。 ( )
。 ( )
(6)平行四边形两对边所在的向量一定是相等向量。 ( )
解:(1)错。因为两个向量的方向相同或相反叫共线向量,而两个向量所在直线平行时也称它们为共线向量,即共线向量不一定在同一条直线上。
(2)错。单位向量是指长度等于1个单位长度的向量,而其方向不一定相同,它不符合相等向量的意义。
(3)错。注意到零向量与任意向量共线,当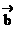 为零向量时,它不成立。(想一想:你能举出反例吗?又若
为零向量时,它不成立。(想一想:你能举出反例吗?又若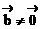 时,此结论成立吗?)
时,此结论成立吗?)
(4)对。因共线向量又叫平行向量。
(5)错。平行向量与平行直线是两个不同概念,AB、CD也可能是同一条直线上。
(6)错。平行四边形两对边所在的向量也可能方向相反。
6.向量方法证明:对角线互相平分的四边形是平行四边形。
已知四边形ABCD,AC与BD交于O,AO=OC,DO=OB,
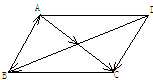 求证:ABCD是平行四边形。
求证:ABCD是平行四边形。
证:如图:∵
又由已知 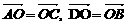
∴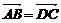 ,故AB与DC平行且相等,所以ABCD是平行四边形。
,故AB与DC平行且相等,所以ABCD是平行四边形。
★ 抢 分 频 道 ★
基础巩固训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com