
题目列表(包括答案和解析)
3.实数与向量的积:
(1)定义:实数λ与向量a的积是一个向量,记作λa,规定:|λa|=|λ||a|.当λ>0时,λa的方向与a的方向相同;当λ<0时,λa的方向与a的方向相反;当λ=0时,λa与a平行.
(2)运算律:λ(μa)=(λμ)a, (λ+μ)a=λa+μa, λ(a+b)=λa+λb.
特别提醒:
1) 向量的加、减及其与实数的积的结果仍是向量。
2) 重要定理:
向量共线定理:向量b与非零向量a共线的充要条件是有且仅有一个实数λ,使得b=λa,即b∥a b=λa(a≠0).
b=λa(a≠0).
★ 重 难 点 突 破 ★
2.向量的减法:
(1)定义:求两个向量差的运算,叫做向量的减法.
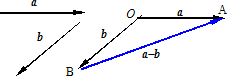 已知向量a、b,求作向量
已知向量a、b,求作向量
∵(a-b) + b = a + (-b) + b = a + 0 = a
减法的三角形法则作法:在平面内取一点O,
作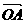 = a,
= a, 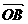 = b, 则
= b, 则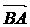 = a - b
= a - b
即a - b可以表示为从向量b的终点指向向量a的终点的向量
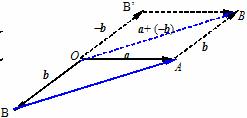 注意:
注意:
1) 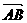 表示a - b
表示a - b 强调:差向量“箭头”指向被减数
强调:差向量“箭头”指向被减数
2) 用“相反向量”定义法作差向量,a - b = a + (-b)
显然,此法作图较繁,但最后作图可统一
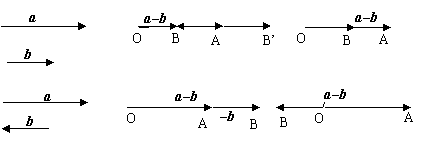 a∥b∥c
a - b = a
+ (-b) a - b
a∥b∥c
a - b = a
+ (-b) a - b
(2)法则:____三角形法则_______
1.向量的加法:
(1)定义:求两个向量和的运算,叫做向量的加法.
如图,已知向量a,b, 在平面内任取一点
在平面内任取一点 ,作
,作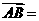 a,
a,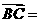 b,则向量
b,则向量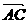 叫做a与b的和,记作a+b,即 a+b
叫做a与b的和,记作a+b,即 a+b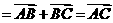
特殊情况: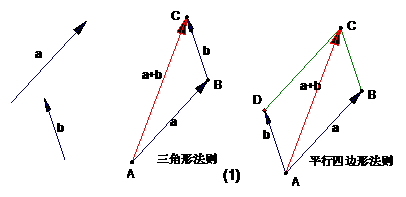

对于零向量与任一向量a,有 a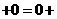 a
a 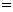 a
a
(2)法则:____三角形法则_______,_____平行四边形法则______
(3)运算律:____ a+b=b+a;_______,____(a+b)+c=a+(b+c)._______
2.向量的线性运算
1.平面向量的有关概念:
(1)向量的定义:既有____大小又有方向_________的量叫做向量.
(2)表示方法:用有向线段来表示向量.有向线段的____长度_____表示向量的大小,用_____箭头所指的方向____表示向量的方向.用字母a,b,…或用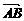 ,
,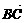 ,…表示.
,…表示.
特别提醒:
1)
模:向量的长度叫向量的模,记作|a|或|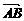 |.
|.
2) 零向量:长度为零的向量叫做零向量,记作0;零向量的方向不确定.
3) 单位向量:长度为1个长度单位的向量叫做单位向量.
4) 共线向量:方向相同或相反的向量叫共线向量,规定零向量与任何向量共线.
5) 相等的向量:长度相等且方向相同的向量叫相等的向量.
10.已知点O(0,0),A(1,2),B(4,5),且 =+t.
(1) 当t变化时,点P是否在一条定直线上运动?
(2) 当t取何值时,点P在y轴上?
(3) OABP能否成为平行四边形?若能求出相应的t值;若不能,请说明理由.
解:(1)由= +t可得 = t,∥,又、都过A点,故A、P、B三点在同一条直线上,而A、B为定点,所以P点恒在直线AB上运动.(2)=(1+3t,2+3t),若P在y轴上,则1+3t=0,t=-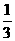 .(3)A、B、P三点在同一条直线上,OABP不可能为平行四边形,若用 = 可列方程组,但方程组无解.
.(3)A、B、P三点在同一条直线上,OABP不可能为平行四边形,若用 = 可列方程组,但方程组无解.
9.已知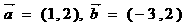 ,当实数
,当实数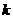 取何值时,
取何值时,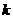
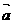 +2
+2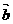 与2
与2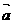 -4
-4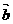 平行?
平行?
[解析]方法一: ∵ 2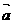 -4
-4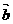
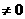 ,∴ 存在唯一实数
,∴ 存在唯一实数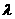 使
使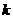
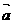 +2
+2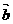 =
=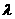
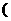 2
2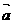 -4
-4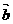 )
)
将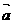 、
、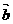 的坐标代入上式得(
的坐标代入上式得(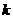 -6,2
-6,2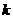 +4)=
+4)=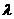
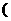 14,-4)
14,-4)
得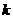 -6=14
-6=14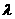 且2
且2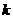 +4= -4
+4= -4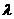 ,解得
,解得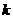 = -1
= -1
方法二:同法一有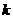
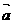 +2
+2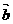 =
=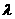 (2
(2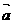 -4
-4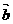 ),即(
),即(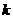 -2
-2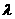
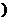
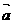 +(2+4
+(2+4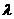
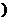
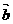 =0
=0
∵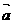 与
与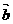 不共线,∴
不共线,∴ 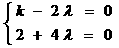 ∴
∴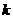 = -1
= -1
8.(江西省鹰潭市2008届高三第一次模拟)已知向量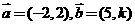 ,若
,若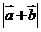 不超过5,则
不超过5,则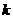 的取值范围是 .
的取值范围是 .
答案: [-6,2]
解析: 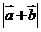 =
=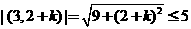 解得
解得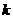 的取值范围是[-6,2]
的取值范围是[-6,2]
7.(广东省深圳外国语学校2009届高三统测(数学理))
已知向量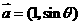 ,
,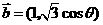 ,则
,则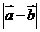 的最大值为 .
的最大值为 .
答案:2 解析: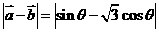 =
=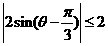 .
.
6.(2009年广东省广州市高三年级调研测试数 学(理 科))
如图,在△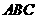 中,已知
中,已知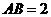 ,
,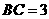 ,
,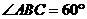 ,
,
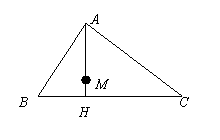
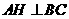 于
于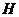 ,
,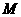 为
为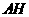 的中点,若
的中点,若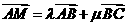 ,
,
则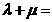 .
.
答案: 解析:
解析: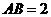 ,
,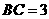 ,
,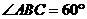
所以BH=1,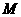 为
为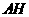 的中点,所以
的中点,所以
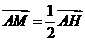
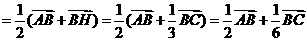
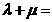

综合拔高训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com