
题目列表(包括答案和解析)
5.数列1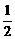 ,3
,3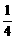 ,5
,5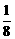 ,7
,7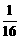 ,…,(2n-1)+
,…,(2n-1)+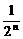 的前n项之和为Sn,则Sn等于
的前n项之和为Sn,则Sn等于
A.n2+1-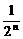 B.2n2-n+1-
B.2n2-n+1-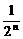 C.n2+1-
C.n2+1-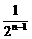 D.n2-n+1-
D.n2-n+1-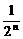
4.已知a=(2,1),b=(x,1),且a+b与2a-b平行,则x等于
A.10 B.-10 C.2 D.-2
3.双曲线kx2+5y2=5的一个焦点是(0,2),则k等于
A.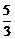 B.-
B.-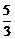 C.
C.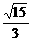 D.-
D.-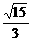
2.已知sinθ=-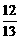 ,θ∈(-
,θ∈(-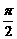 ,0),则cos(θ-
,0),则cos(θ-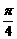 )的值为
)的值为
A.-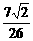 B.
B.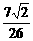 C.-
C.-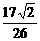 D.
D.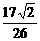
1.已知集合P={(x,y)|y=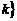 ,Q={(x,y)|y=ax+
,Q={(x,y)|y=ax+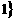 ,且P∩Q=
,且P∩Q=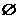 ,那么k的取值范围是
,那么k的取值范围是
A.(-∞,1) B.(-∞,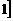 C.(1,+∞) D.(-∞,+∞)
C.(1,+∞) D.(-∞,+∞)
20.(本小题满分16分)
设f1(x)=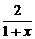 ,定义fn+1 (x)=f1[fn(x)],an=
,定义fn+1 (x)=f1[fn(x)],an=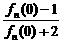 ,其中n∈N*.
,其中n∈N*.
(1)求数列{an}的通项公式;
(2)若T2n=a1+2a2+3a3+…+2na2n,Qn=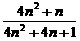 ,其中n∈N*,试比较9T2n与Qn的大小,并说明理由.
,其中n∈N*,试比较9T2n与Qn的大小,并说明理由.
19.(本小题满分14分)
已知点H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足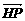 ·
·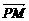 =0,
=0,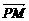 =-
=-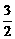
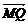 ,
,
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-1,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使得△ABE为等边三角形,求x0的值.
18.(本小题满分13分)
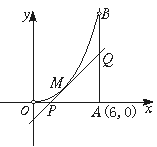 如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
如图所示,曲线段OMB是函数f(x)=x2(0<x<6)的图象,BA⊥x轴于A,曲线段OMB上一点M(t,f(t))处的切线PQ交x轴于点P,交线段AB于点Q,
(1)试用t表示切线PQ的方程;
(2)试用t表示出△QAP的面积g(t);若函数g(t)在(m,n)上单调递减,试求出m的最小值;
(3)若S△QAP∈[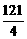 ,64],试求出点P横坐标的取值范围.
,64],试求出点P横坐标的取值范围.
17.(本小题满分13分)
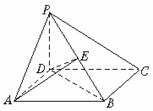 如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
如图,四棱锥P-ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.
求证:(1)平面PAC⊥平面PBD;
(2)求PC与平面PBD所成的角;
(3)在线段PB上是否存在一点E,使得PC⊥平面ADE?若存在,请加以证明,并求此时二面角A-ED-B的大小;若不存在,请说明理由.
16.(本小题满分12分)
已知平面向量a=(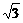 ,-1),b=(
,-1),b=(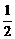 ,
,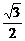 ),若存在不为零的实数k和角α,使向量c=a+ (sinα-3)b,d=-ka+(sinα)b,且c⊥d,试求实数k的取值范围.
),若存在不为零的实数k和角α,使向量c=a+ (sinα-3)b,d=-ka+(sinα)b,且c⊥d,试求实数k的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com