
题目列表(包括答案和解析)
17.
(2001上海(19)14分)用一块钢锭浇铸一个厚度均匀,且全面积为2平方米的正四棱锥形有盖容器(如图),设容器的高为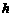 米,盖子边长为
米,盖子边长为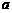 米.
(1)求
米.
(1)求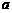 关于
关于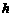 的函数解析式;
(2)设容器的容积为
的函数解析式;
(2)设容器的容积为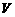 立方米,则当
立方米,则当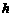 为何值时,
为何值时,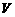 最大?求出
最大?求出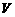 的最大值.(求解本题时,不计容器的厚度)
的最大值.(求解本题时,不计容器的厚度)
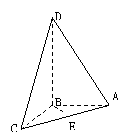
16. 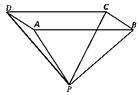 (2000上海(18)12分)如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成角的大小为arccos
(2000上海(18)12分)如图所示四面体ABCD中,AB、BC、BD两两互相垂直,且AB=BC=2,E是AC中点,异面直线AD与BE所成角的大小为arccos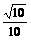 ,求四面体ABCD的体积
,求四面体ABCD的体积
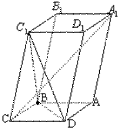
15. (2000⒅12分)如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°
⑴证明:C1C⊥BD;
⑵假定CD=2,CC1=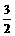 ,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
⑶当
,记面C1BD为α,面CBD为β,求二面角α-BD-β的平面角的余弦值;
⑶当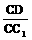 的值为多少时,能使A1C⊥平面C1BD?请给出证明.
的值为多少时,能使A1C⊥平面C1BD?请给出证明.
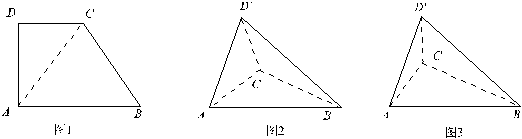
14. (2000安徽(20)12分)在直角梯形ABCD中,∠D=∠BAD=90°,AD=DC=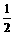 AB=a(如图1).将△ADC沿AC折起,使D到D′.记面ACD′为α,面ABC为β,面BCD′为γ.
(I)若二面角α-AC-β为直二面角(如图2),求二面角β-BC-γ的大小;
(II)若二面角α-AC-β为60°(如图3),求三棱锥D′-ABC的体积.
AB=a(如图1).将△ADC沿AC折起,使D到D′.记面ACD′为α,面ABC为β,面BCD′为γ.
(I)若二面角α-AC-β为直二面角(如图2),求二面角β-BC-γ的大小;
(II)若二面角α-AC-β为60°(如图3),求三棱锥D′-ABC的体积.
13. (99(21)12分)如图,已知正四棱柱ABCD-A′B′C′D′,点E在棱D′D上, 截面EAC∥D′B,且面EAC与底面ABCD所成的角为45°,AB=a (1)求截面EAC的面积 (2)求异面直线A′B′与AC之间的距离 (3)求三棱锥B′-EAC的体积
12. (98(23)12分)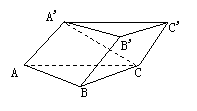
 已知斜三棱柱ABC-A′B′C′的侧面A′ACC′与底面ABC垂直,∠ABC=90°,BC=2,AC=2
已知斜三棱柱ABC-A′B′C′的侧面A′ACC′与底面ABC垂直,∠ABC=90°,BC=2,AC=2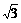 且AA′⊥A′C,AA′=A′C.
①求侧棱AA′与底面ABC所成角的大小;
②求侧面A′ABB′与底面ABC所成二面角的大小;
③求顶点C到侧面A′ABB′的距离.
且AA′⊥A′C,AA′=A′C.
①求侧棱AA′与底面ABC所成角的大小;
②求侧面A′ABB′与底面ABC所成二面角的大小;
③求顶点C到侧面A′ABB′的距离.
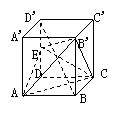
11. 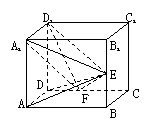 (97(23)12分)如图,在正方体ABCD-A1B1C1D1中,E,F分别是BB1、CD的中点.
Ⅰ.证明AD⊥D1F;
Ⅱ.求AE与D1F所成的角;
Ⅲ.证明面AED⊥面A1FD1;
Ⅳ.设AA1=2,求三棱锥F-A1ED1的体积VF-A1ED1.
(97(23)12分)如图,在正方体ABCD-A1B1C1D1中,E,F分别是BB1、CD的中点.
Ⅰ.证明AD⊥D1F;
Ⅱ.求AE与D1F所成的角;
Ⅲ.证明面AED⊥面A1FD1;
Ⅳ.设AA1=2,求三棱锥F-A1ED1的体积VF-A1ED1.
10. (96(22)12分)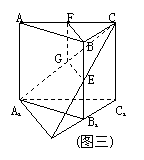
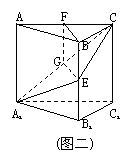
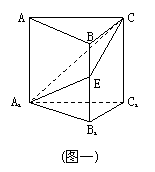 如图:在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
Ⅰ.求证:BE=EB1;
Ⅱ.若AA1=A1B1,求平面A1EC与平面所成二面角(锐角)的度数.
注意:在下面横线上填上适当内容,使之成为Ⅰ的完整证明,并解答Ⅱ.
Ⅰ.证明:在截面A1EC内,过E作EG⊥A1C,G是垂足,
①∵_____________,
∴EG⊥侧面AC1;取AC的中点F,连结BF,FG,
由AB=BC得BF⊥AC,
②∵_____________,
∴BF⊥侧面AC1;得BF∥EG,
则BF,EG确定一个平面,交侧面AC1于FG,
③∵_____________,
∴BF∥FG,四边形BEGF是平行四边形,BE=FG.
④∵_____________,
∴FG∥AA1,△AA1C∽△FGC
⑤∵_____________,
∴FG=
如图:在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
Ⅰ.求证:BE=EB1;
Ⅱ.若AA1=A1B1,求平面A1EC与平面所成二面角(锐角)的度数.
注意:在下面横线上填上适当内容,使之成为Ⅰ的完整证明,并解答Ⅱ.
Ⅰ.证明:在截面A1EC内,过E作EG⊥A1C,G是垂足,
①∵_____________,
∴EG⊥侧面AC1;取AC的中点F,连结BF,FG,
由AB=BC得BF⊥AC,
②∵_____________,
∴BF⊥侧面AC1;得BF∥EG,
则BF,EG确定一个平面,交侧面AC1于FG,
③∵_____________,
∴BF∥FG,四边形BEGF是平行四边形,BE=FG.
④∵_____________,
∴FG∥AA1,△AA1C∽△FGC
⑤∵_____________,
∴FG=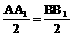 ,即BE=
,即BE=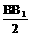 ,故BE=EB1.
,故BE=EB1.
9. (95上海)四棱锥P-ABCD中,底面是矩形,AB=3,AD=1,又PA⊥AB,PA=4,∠PAD=60° ⑴求四棱锥P-ABCD的体积; ⑵求二面角P-BC-D的大小(用反三角函数表示)
8. (95(23)12分)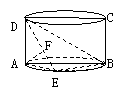 如图:圆柱的轴截面ABCD是正方形,
点E在底面圆周上,AF⊥DE,F是垂足
Ⅰ.求证:AF⊥DB;
Ⅱ.如果圆柱与三棱锥D-ABC的体积比等于3π,
求直线DE与平面ABCD所成的角.
如图:圆柱的轴截面ABCD是正方形,
点E在底面圆周上,AF⊥DE,F是垂足
Ⅰ.求证:AF⊥DB;
Ⅱ.如果圆柱与三棱锥D-ABC的体积比等于3π,
求直线DE与平面ABCD所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com