
题目列表(包括答案和解析)
21、正方形ABCD和正方形ABEF折成一个二面角,M、N分别是对角线AC和BF上的点,且AM=FN(如图),求证:MN//平面BEC.
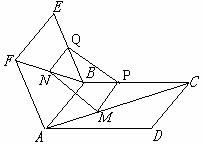 证明:如图,分别过M、N作
证明:如图,分别过M、N作
MP∥DC交BC于P,NQ ∥EF交
EB于Q,连接PQ ∵EF∥AB∥CD,∴MP∥NQ
又∵AM=FN,∴在正方形ABEF
和正方形ABCD中,MP=NQ
∴ 四边形 MPQN为平行四边形
∴MN∥PQ,∵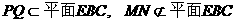
∴MN∥平面EBC
20、将两副三角板放成如图所示的形状,使二面角D-AC-B成直二面角。
已知:BC=CD,∠ACD=∠ABC=900.求:二面角C-AB-D的大小。
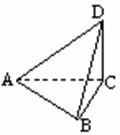 证:如图∵平面ACD^平面ABC,CD^AC,
证:如图∵平面ACD^平面ABC,CD^AC,
∴CD^平面ABC.
∵斜线BD在平面ABD上的射影为BC,AB^BC,
∴AB^BD.即∠DBC为二面角
C-AB-D的平面角。
∵BC=CD,CD^BC,∴∠DBC=450翰林汇
19、已知数列{an}满足a1=2,对于任意的n∈N,都有an>0,
且(n+1)a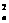 +anan+1-na
+anan+1-na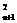 =0,又知数列{bn}:b1=2n-1+1
(1)求数列{an}的通项an以及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn和Tn的大小关系,并说明理由.
=0,又知数列{bn}:b1=2n-1+1
(1)求数列{an}的通项an以及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn和Tn的大小关系,并说明理由.
解:(Ⅰ)∵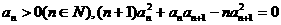
∴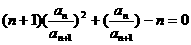 。
。
∴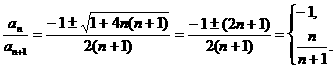
∴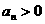 ,∴
,∴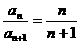 。 即
。 即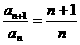 。
。
∴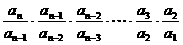
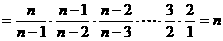 。
。
∴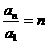 ,∴又
,∴又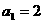 ,∴
,∴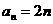 。
。
∴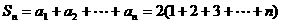
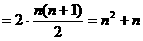 。
。
(Ⅱ)∵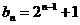 ,
,
∴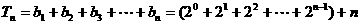
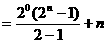
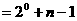 。
。
(Ⅲ)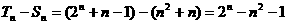
当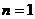 时,
时,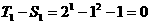 ,∴
,∴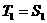 ;
;
当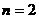 时,
时,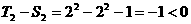 ,∴
,∴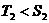 ;
;
当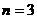 时,
时,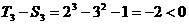 ,∴
,∴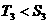 ;
;
当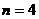 时,
时,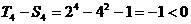 ,∴
,∴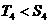 ;
;
当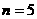 时,
时,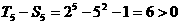 ,∴
,∴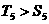 ;
;
当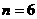 时,
时,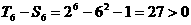 ,∴
,∴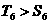 。
。
猜想:当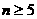 时,
时,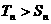 。 即
。 即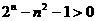 。亦即
。亦即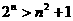 。
。
下面用数学归纳法证明:
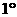 当
当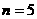 时,前面已验证成立;
时,前面已验证成立;
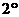 假设
假设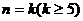 时,
时,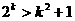 成立,那么当
成立,那么当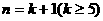 时,
时,
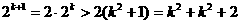
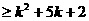
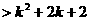
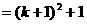 。
。
∴当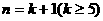 时,
时,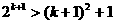 也成立。
也成立。
由以上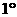 、
、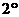 可知,当
可知,当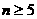 时,有
时,有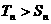 ;当
;当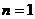 时,
时,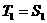 ;
;
当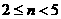 时,
时,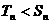 。
。
18、在工厂生产中,若机器更新过早,则生产潜力未能充分发挥而造成浪费;若更新过迟,老机器生产效率低,维修与损耗费用大,也会造成浪费.因此,需要确定机器使用的最佳年限(即机器使用多少年平均费用最小) 某工厂用7万元购买了一台新机器,运输安装费2千元,每年投保、动力消耗固定的费用为2千元;每年的保养、维修、更换易损件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,……,即每年增加1千元,问这台机器的最佳使用年限是多少年?并求出年平均费用的最小值.
解:设使用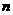 年为最佳年限,则每年的平均费用
年为最佳年限,则每年的平均费用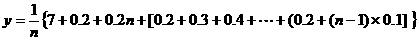
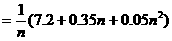
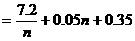
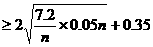
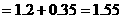 (万元)。
(万元)。
当且仅当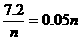 ,即
,即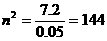 ,即
,即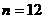 时取等号。
时取等号。
答:这台机器最佳使用年限为12年,且年平均费用的最小值为1.55万元。
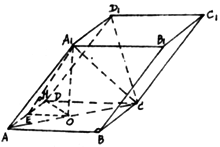
17、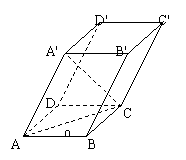 如图,平行六面体ABCD-A'B'C'D'中,AC=2
如图,平行六面体ABCD-A'B'C'D'中,AC=2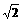 ,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
(1)求侧棱AA'与底面ABCD所成角的大小;
(2)求侧面A'ADD'底面ABCD所成二面角的正切值;
(3)求四棱锥C-A'ADD'的体积.
,BC=AA'=A'C=2,∠ABC=90°,点O是点A'在底面ABCD上的射影,且点O恰好落在AC上.
(1)求侧棱AA'与底面ABCD所成角的大小;
(2)求侧面A'ADD'底面ABCD所成二面角的正切值;
(3)求四棱锥C-A'ADD'的体积.
解:(I)连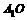 ,则
,则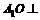 平面
平面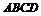 于
于
∴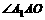 就是侧棱
就是侧棱 与底面
与底面 所成的角
所成的角
在 中,
中,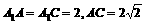
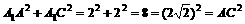
∴ 是等腰直角三角形
是等腰直角三角形
∴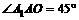 ,即侧棱
,即侧棱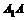 与底面
与底面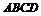 所成角为45°,
所成角为45°,
(II)在等腰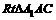 中,
中,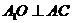 ,∴
,∴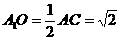 ,且O为AC中点,
,且O为AC中点,
过O作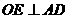 于E,连
于E,连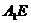 。∵
。∵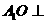 平面ABCD于O,
平面ABCD于O,
由三垂线定理,知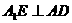 ,
,
∴∠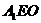 是侧面
是侧面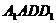 与底面ABCD所成二面角的平面角。
与底面ABCD所成二面角的平面角。
∵∠ABC=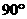 ,
,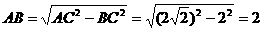 ,∴底面ABCD是正方形。
,∴底面ABCD是正方形。
∴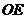
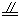
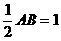 。 在
。 在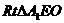 中,
中,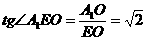 。
。
即所求二面角的正切值为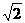 。
。
(Ⅲ)由(Ⅱ)知,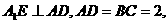
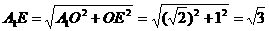 。
。
∴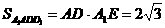 。
。
∵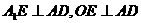 ,∴
,∴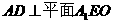 。
。
∵ ,∴平面
,∴平面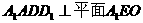 ,它们的交线是
,它们的交线是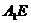 。
。
过O作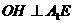 ,则
,则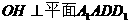 。
。
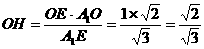 。
。
又∵ 的中点,∴点C到平面
的中点,∴点C到平面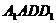 的距离
的距离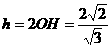 。
。
∴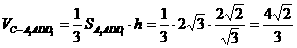 。
。
另解: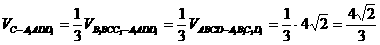 。
。
16、已知复数z1=2-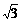 x+xi,z2=
x+xi,z2=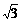 y-1+(
y-1+(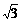 -y)i,x、y属于R,若|z1|=|z2|且argz1/z2=90º,求
-y)i,x、y属于R,若|z1|=|z2|且argz1/z2=90º,求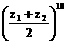 的值
的值
解:∵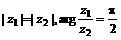 ∴
∴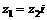
∴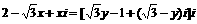
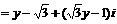 ∴
∴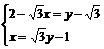
解得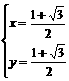
∴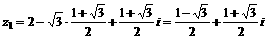 ,
,
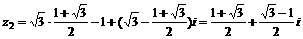
∴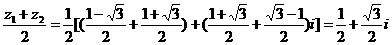
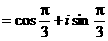
∴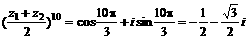
15、在三角形ABC中,三内角满足A+C=2B,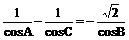 ,求cos
,求cos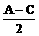 的值
的值
解:∵A+C=2B,∴A+C=120°,B=60°
又∵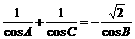 ,∴
,∴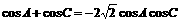
∴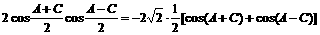
即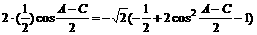
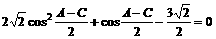
令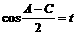 ,则上式为
,则上式为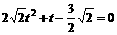
∴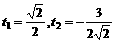
∵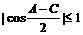 ,∴
,∴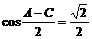
14、解关于x的不等式:loga(x2-x-2)>loga(x-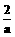 )+1(a>0,a≠1)
)+1(a>0,a≠1)
解:原不等式等价于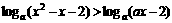 ……①
……①
1°当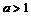 时,①式可化为
时,①式可化为
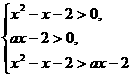 从而
从而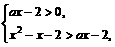 即
即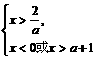
∴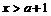
2°当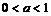 时,①式可化为
时,①式可化为
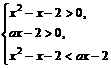 从而
从而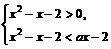 即
即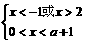 ∴
∴ Φ
Φ
综上所述,当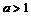 时,原不等式的解集为
时,原不等式的解集为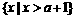 ;当
;当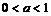 时,不等式的解集为Φ
时,不等式的解集为Φ
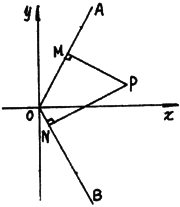
13、已知:如图,射线OA为y=2x(x>0),射线OB为y= –2x(x>0),动点P(x, y)在 的内部,
的内部,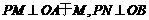 于N,四边形ONPM的面积为2..
于N,四边形ONPM的面积为2..
(I)动点P的纵坐标y是其横坐标x的函数,求这个函数y=f(x)的解析式;
 (II)确定y=f(x)的定义域.
(II)确定y=f(x)的定义域.
解:(Ⅰ)设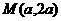 ,
,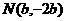
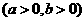 .
.
则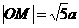 ,
,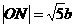
由动点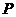 在
在 的内部,得
的内部,得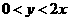 .
.
∴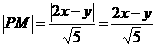 ,
,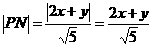
∴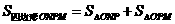
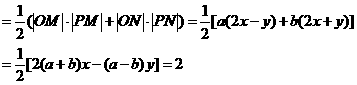
∴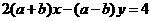 ①
①
又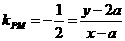 ,
,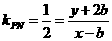
分别解得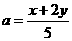 ,
,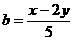
代入①式消去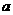 、
、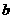 ,并化简得
,并化简得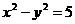 .
.
∵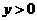 ,∴
,∴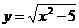 .
.
(Ⅱ)由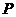 在
在 内部,得
内部,得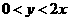 .
.
又垂足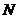 必须在射线
必须在射线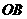 上,否则
上,否则 、
、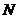 、
、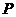 、
、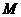 四点不能构成四边形,所以还必须满足条件
四点不能构成四边形,所以还必须满足条件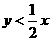
∴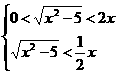
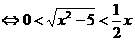
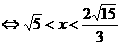
所以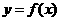 的定义域为
的定义域为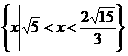
12、已知水渠在过水断面面积为定值的情况下,过水湿周越小,其流量越大.现有以下两种设计,如图:
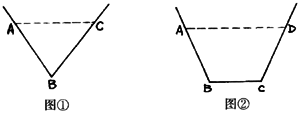
图①的过水断面为等腰△ABC,AB=BC,过水湿周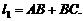
图②的过水断面为等腰梯形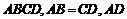 ∥
∥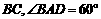 ,过水湿周
,过水湿周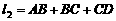 .若
.若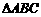 与梯形ABCD的面积都为S,
与梯形ABCD的面积都为S,
(I)分别求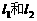 的最小值;
的最小值;
(II)为使流量最大,给出最佳设计方案.
解(Ⅰ)在图①中,设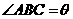 ,
,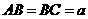 .
.
则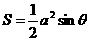 .由于
.由于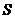 、
、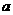 、
、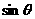 皆为正值,可解得
皆为正值,可解得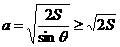 .
.
当且仅当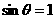 ,即
,即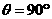 时取等号.
时取等号.
所以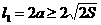 .
.
在图②中,设 ,
,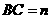 .
.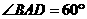 可求得
可求得
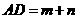 ,
,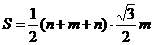
解得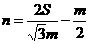 .
.
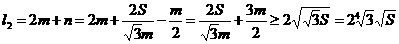 .
.
当且仅当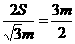 ,即
,即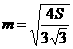 时取等号.
时取等号.
(Ⅱ)由于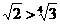 ,则
,则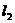 的最小值小于
的最小值小于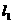 的最小值.
的最小值.
所以在方案②中当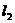 取得最小值时的设计为最佳方案.
取得最小值时的设计为最佳方案.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com