
题目列表(包括答案和解析)
43、α,β是两个不重合的平面,在α上取4个点,在β上取3个点,则由这些点最多可以确定平面( )。 (A)35个 (B)30个 (C)32个 (D)40个
提示:运用排列组合以及平面的性质进行分析。
42、已知函数f(x)在定义域R内是减函数且f(x)<0,则函数g(x)=x2 f(x)的单调情况一定是( )。
(A)在R上递减 (B)在R上递增 C)在(0,+∞)上递减 (D)在(0,+∞)上递增
提示:先选定区间(0,+∞)分析其增减性,再结合筛选法,对余下的部分,取特殊值进行验证。
41. 已知函数y=|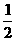 +cos(2x+
+cos(2x+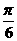 )|, (
)|, (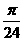 ≤x≤
≤x≤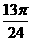 ), 下列关于此函数的最值及相应的x的取值的结论中正确的是( )。
), 下列关于此函数的最值及相应的x的取值的结论中正确的是( )。
(A)ymax=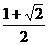 ,x=
,x=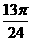 (B)ymax=
(B)ymax=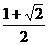 ,x=
,x=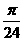
(C)ymin=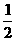 ,x=
,x=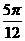 (D)ymin=0,x=
(D)ymin=0,x=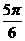
提示:对余弦函数最值进行分析。
40、能够使得sinx>0和tgx>0同时成立的角x的集合是( )。
(A){x|0<x<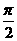 } (B){x|0<x<
} (B){x|0<x<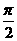 或
或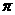 <x<
<x<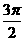 }
}
(C){x|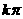 <x<
<x<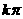 +
+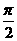 ,k∈Z} (D){x|2
,k∈Z} (D){x|2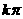 <x<2
<x<2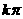 +
+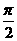 ,k∈Z}
,k∈Z}
提示:通过不同象限,三角函数值的正负不同的特点,进行分析。
39、设A={x| x2+px+q=0},B={x| x2+(p-1)x+2q=0},若A∩B={1},则( )。
(A)
A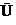 B (B)A
B (B)A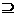 B (C)A∪B ={1, 1, 2}
B (C)A∪B ={1, 1, 2} (D)A∪B=(1,-2)
(D)A∪B=(1,-2)
提示:考察集合与集合的关系。
38、有下列三个对应:①A=R+,B=R,对应法则是“取平方根”;②A={矩形},B=R+,对应法则是“求矩形的面积”;③A={非负实数},B=(0,1),对应法则是“平方后与1的和的倒数”,其中从A到B的对应中是映射的是( )。
(A)② (B)②,③ (C)①,②,③ (D)①,②
提示:映射的概念。
37、在正方体AC1中,过与顶点A相邻的三个顶点作平面α,过与顶点C1相邻的三个顶点作平面β,那么平面α与平面β的位置关系是( )
(A)垂直 (B)平行 (C)斜交 (D)斜交或平行
提示:作图后,找线线关系,由线线平行得出线面平行,从而求得面面平行。
36、直线x-ay+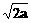 =0(a>0且a≠1)与圆x2+y2=1的位置关系是( )
=0(a>0且a≠1)与圆x2+y2=1的位置关系是( )
(A)相交 (B)相切 (C)相离 (D)不能确定
提示:运用点到直线的距离公式,比较半径与距离的大小。
35、在-8,-6,-4,-2,0,1,3,5,7,9这十个数中,任取两个作为虚数a+b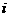 的实部和虚部(a, b∈R, a≠b),则能组成模大于5的不同虚数的个数有( )。
的实部和虚部(a, b∈R, a≠b),则能组成模大于5的不同虚数的个数有( )。
(A)64个 (B)65个 (C)72个 (D)73个
提示:虚部不能为0,模大于5,最好用“树图”来讨论。
34、在(2-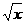 )8的展开式中,第七项是( )
)8的展开式中,第七项是( )
(A)112x3 (B)-112x3 (C)16x3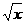 (D)-16x3
(D)-16x3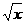
提示:运用二项展开式的通项公式,注意:r =6。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com