
题目列表(包括答案和解析)
6.(理)在正方体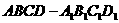 中,M,N分别为棱
中,M,N分别为棱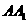 和
和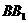 之中点,则sin(
之中点,则sin(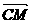 ,
,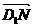 )的值为( )
)的值为( )
A.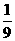 B.
B.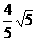 C.
C.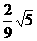 D.
D.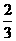
(文)已知三棱锥S-ABC中,SA,SB,SC两两互相垂直,底面ABC上一点P到三个面SAB,SAC,SBC的距离分别为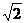 ,1,
,1,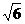 ,则PS的长度为( )
,则PS的长度为( )
A.9 B.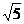 C.
C.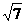 D.3
D.3
5.与命题“若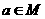 则
则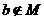 ”的等价的命题是( )
”的等价的命题是( )
A.若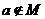 ,则
,则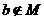 B.若
B.若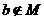 ,则
,则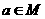
C.若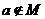 ,则
,则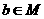 D.若
D.若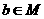 ,则
,则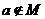
4.若函数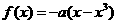 的递减区间为(
的递减区间为(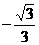 ,
,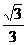 ),则a的取值范围是( )
),则a的取值范围是( )
A.a>0 B.-1<a<0 C.a>1 D.0<a<1
3.已知数列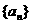 前n项和为
前n项和为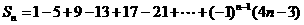 ,则
,则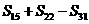 的值是( )
的值是( )
A.13 B.-76 C.46 D.76
2.(理)复数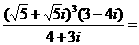 ( )
( )
A.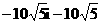 B.
B.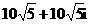 C.
C.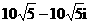 D.
D.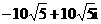
(文)点M(8,-10),按a平移后的对应点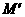 的坐标是(-7,4),则a=( )
的坐标是(-7,4),则a=( )
A.(1,-6) B.(-15,14) C.(-15,-14) D.(15,-14)
1.(理)全集设为U,P、S、T均为U的子集,若 (
(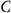
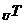 )=(
)=(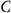
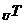 )
)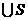 则( )
则( )
A. B.P=T=S C.T=U D.
B.P=T=S C.T=U D.
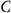
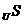 =T
=T
(文)设集合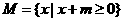 ,
,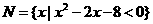 ,若U=R,且
,若U=R,且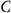
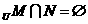 ,则实数m的取值范围是( )
,则实数m的取值范围是( )
A.m<2 B.m≥2 C.m≤2 D.m≤2或m≤-4
22.(14分)已知等差数列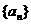 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列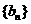 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,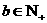 ,且
,且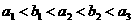 .
.
(1)求a的值;
(2)若对于任意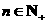 ,总存在
,总存在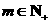 ,使
,使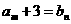 ,求b的值;
,求b的值;
(3)在(2)中,记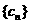 是所有
是所有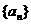 中满足
中满足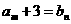 ,
, 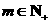 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记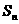 为
为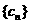 的前n项和,
的前n项和,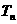
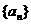 的前n项和,求证:
的前n项和,求证: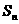 ≥
≥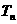
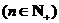 .
.
21.(12分)已知椭圆方程为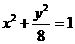 ,射线
,射线 (x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(x≥0)与椭圆的交点为M,过M作倾斜角互补的两条直线,分别与椭圆交于A、B两点(异于M).
(1)求证直线AB的斜率为定值;
(2)求△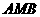 面积的最大值.
面积的最大值.
20.(12分)已知函数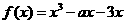 .
.
(1)若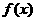 在
在 [1,+∞
[1,+∞ 上是增函数,求实数a的取值范围;
上是增函数,求实数a的取值范围;
(2)若x=3是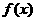 的极值点,求
的极值点,求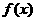 在
在 [1,a]上的最小值和最大值.
[1,a]上的最小值和最大值.
18.(12分)(理)甲、乙队进行篮球总决赛,比赛规则为:七场四胜制,即甲或乙队,谁先累计获胜四场比赛时,该队就是总决赛的冠军,若在每场比赛中,甲队获胜的概率均为0.6,每场比赛必须分出胜负,且每场比赛的胜或负不影响下一场比赛的胜或负.
(1)求甲队在第五场比赛后获得冠军的概率;
(2)求甲队获得冠军的概率;
(文)有甲、乙两只口袋,甲袋装有4个白球2个黑球,乙袋装有3个白球和4个黑球,若从甲、乙两袋中各任取出两球后并交换放入袋中.
(1)求甲袋内恰好有2个白球的概率;
(2)求甲袋内恰好有4个白球的概率;
注意:考生在(19甲)、(19乙)两题中选一题作答,如果两题都答,只以(19甲)计分.
19甲.(12分)如图,正三棱锥P-ABC,PA=4,AB=2,D为BC中点,点E在AP上,满足AE=3EP.
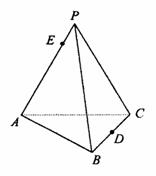
(1)建立适当坐标系,写出A、B、D、E四点的坐标;
(2)求异面直线AD与BE所成的角.
19乙.(12分)如图,长方体 中,
中,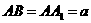 ,
,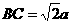 ,M是AD中点,N是
,M是AD中点,N是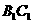 中点.
中点.
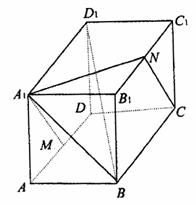
(1)求证: 、M、C、N四点共面;
、M、C、N四点共面;
(2)求证: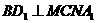 ;
;
(3)求证:平面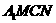 ⊥平面
⊥平面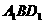 ;
;
(4)求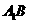 与平面
与平面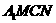 所成的角.
所成的角.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com