
题目列表(包括答案和解析)
根据题设条件的特征进行观察、分析,从而得出正确的结论。
[例4] 设含有10个元素的集合全部子集数为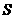 ,其中由3个元素组成的子集数为
,其中由3个元素组成的子集数为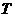 ,则
,则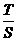 的值为
。
的值为
。
解:由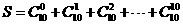 ,
,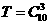 ,故
,故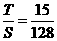 。
。
[类比1] 设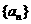 是首项为1的正项数列,且
是首项为1的正项数列,且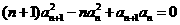 (n=1,2,3,…),
(n=1,2,3,…),
则它们的通项公式是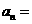 。
。
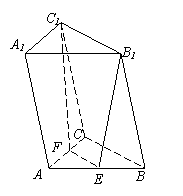
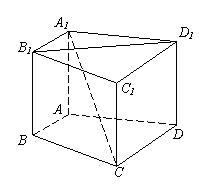 [类比2] 如右图,在直四棱柱
[类比2] 如右图,在直四棱柱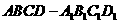
中,当底面四边形满足条件
时,有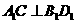 (填上你认为正确的一个条件
(填上你认为正确的一个条件
即可,不必考虑所有可能性的情形)。
[类比3] 椭圆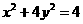 长轴上一个顶点为
长轴上一个顶点为
A, 以A为直角顶点作一个内接于椭圆的等腰直角
三角形,该三角形的面积是 。
[类比4] 已知函数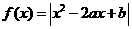
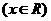 ,给出下列命题:
,给出下列命题:
①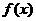 必是偶函数;
必是偶函数;
②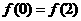 时,
时,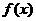 的图象必关于直线
的图象必关于直线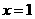 对称;
对称;
③若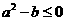 ,则
,则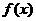 在区间
在区间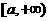 上是增函数;
上是增函数;
④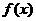 有最大值
有最大值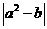 。
。
其中正确的命题的序号是 。
根据题设条件与结论的特殊性,构造出一些新的数学形式,并借助于它认识和解决问题的一种方法。
[例3] 4个不同的小球放入编号为1,2,3,4的4个盒中,则只有1个空盒的放法共有
种(用数字作答)。
解:符合条件的放法是:有一个盒中放2个球,有2个盒中各放1个球。因此可先将球
分成3堆(一堆2个,其余2堆各1个,即构造了球的“堆”),然后从4个盒中选出3个盒
放1堆球,依分步计算原理,符合条件的放法有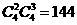 (种)。
(种)。
[类比1] 在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=
PC=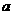 ,那么这个球面面积是
。
,那么这个球面面积是
。
根据题设条件的特征,选取恰当的特殊值进行计算,从而得出探求的结论。
[例2] 不论 取何值,直线
取何值,直线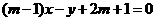 恒过一定点,这个定点坐标是 .
恒过一定点,这个定点坐标是 .
 解:取
解:取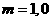 两个值分别代入直线得不同方程为
两个值分别代入直线得不同方程为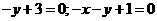 。解得交点坐标为
。解得交点坐标为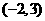 。
。
[类比1] 如图所示,三棱柱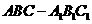 中,若E、
中,若E、
F分别为AB、AC的中点,平面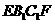 将三棱柱分成
将三棱柱分成
体积为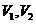 两部分,则
两部分,则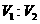 =
。
=
。
[类比2] 设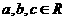 ,且
,且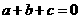 ,则直线
,则直线
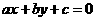 通过的定点为
。
通过的定点为
。
[类比3] 若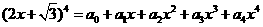 ,则
,则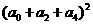
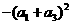
= 。
[类比4] 已知等差数列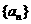 的各项均为正数,且满足
的各项均为正数,且满足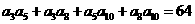 ,
,
则该数列的前12项之和等于 。
从题设条件出发,运用定义、定理、公式、性质、法则等知识,通过变形、推理、计算等,得到正确的结论。
[例1] 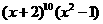 的展开式中
的展开式中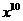 的系数为
。
的系数为
。
解: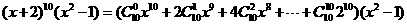
得展开式中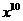 的系数为
的系数为
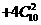 =179。
=179。
[类比1] 已知函数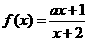 在区间
在区间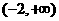 上为增函数,则实数
上为增函数,则实数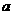 的取值范围
的取值范围
是 。
[类比2] 函数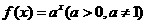 ,在
,在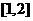 中的最大值比最小值大
中的最大值比最小值大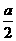 ,则
,则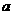 的值
的值
为 。
[类比3] 在等差数列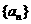 中,若
中,若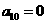 ,则等式
,则等式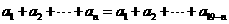
(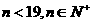 )成立,类比上述性质,相应地,在等比数列
)成立,类比上述性质,相应地,在等比数列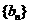 中,若
中,若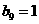 ,则有等
,则有等
式 成立。
[类比4] 已知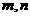 是直线,
是直线,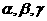 是平面,给出下列命题:
是平面,给出下列命题:
①若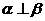 ,
,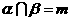 ,
,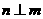 ,则
,则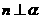 ,或
,或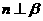 ;
;
②若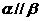 ,
,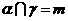 ,
,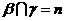 ,则
,则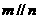 ;
;
③若 不垂直
不垂直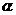 ,则
,则 不可能垂直于
不可能垂直于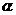 内无数条直线;
内无数条直线;
④若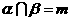 ,
,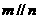 ,且
,且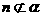 ,
,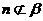 ,则
,则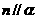 且
且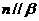 。
。
其中正确的命题的序号是 。(注:把你认为正确的命题的序号都填上)
22.(14分)(理)已知O为△ABC所在平面外一点,且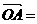 a,
a,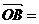 b,
b,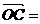 c,OA,OB,OC两两互相垂直,H为△ABC的垂心,试用a,b,c表示
c,OA,OB,OC两两互相垂直,H为△ABC的垂心,试用a,b,c表示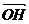 .
.
(文)直线l∶y=ax+1与双曲线C∶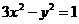 相交于A,B两点.
相交于A,B两点.
(1)a为何值时,以AB为直径的圆过原点;
(2)是否存在这样的实数a,使A,B关于直线x-2y=0对称,若存在,求a的值,若不存在,说明理由.
21.(12分)定义在(-1,1)上的函数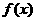 ,(i)对任意x,
,(i)对任意x,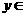 (-1,1)都有:
(-1,1)都有:
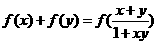 ;(ii)当
;(ii)当 (-1,0)时,
(-1,0)时,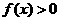 ,回答下列问题.
,回答下列问题.
(1)判断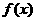 在(-1,1)上的奇偶性,并说明理由.
在(-1,1)上的奇偶性,并说明理由.
(2)判断函数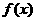 在(0,1)上的单调性,并说明理由.
在(0,1)上的单调性,并说明理由.
(3)(理)若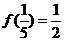 ,试求
,试求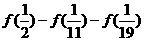 的值.
的值.
20.(12分)线段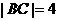 ,BC中点为M,点A与B,C两点的距离之和为6,设
,BC中点为M,点A与B,C两点的距离之和为6,设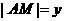 ,
,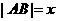 .
.
(1)求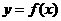 的函数表达式及函数的定义域;
的函数表达式及函数的定义域;
(2)(理)设 ,试求d的取值范围;
,试求d的取值范围;
(文)求y的取值范围.
19.(12分)某森林出现火灾,火势正以每分钟 的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火
的速度顺风蔓延,消防站接到警报立即派消防队员前去,在火灾发生后五分钟到达救火现场,已知消防队员在现场平均每人每分钟灭火 ,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.问应该派多少消防队员前去救火,才能使总损失最少?
,所消耗的灭火材料、劳务津贴等费用为每人每分钟125元,另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元,而烧毁一平方米森林损失费为60元.问应该派多少消防队员前去救火,才能使总损失最少?
18.(12分)如图,在正三棱柱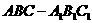 中,M,N分别为
中,M,N分别为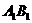 ,BC之中点.
,BC之中点.
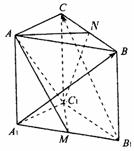
(1)试求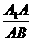 ,使
,使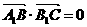 .
.
(2)在(1)条件下,求二面角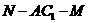 的大小.
的大小.
17.(12分)从一批含有13只正品,2只次品的产品中不放回地抽取3次,每次抽取一只,设抽得次品数为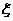 .
.
(1)求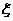 的分布列;
的分布列;
(2)求E(5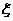 -1).
-1).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com