
题目列表(包括答案和解析)
8.新教材同学做:
某校高二(8)班四位同学的数学期中、期末和平时成绩可分别用矩阵
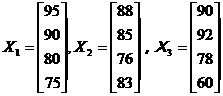 表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵
表示,总评成绩分别按期中、期末和平时成绩的30%、40%、30%的总和计算,则四位同学总评成绩的矩阵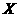 可用
可用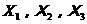 表示为
表示为 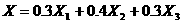 。
。
老教材同学做:
某足球队共有11名主力队员和3名替补队员参加一场足球比赛,其中有2名主力和1名替补队员不慎误服违禁药物,依照比赛规定,比赛后必须随机抽取2名队员的尿样化验,则能查到服用违禁药物的主力队员的概率为 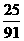 。(结果用分数表示)
。(结果用分数表示)
7.已知函数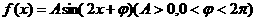 ,若对任意
,若对任意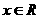 有
有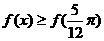 成立,则方程
成立,则方程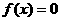 在
在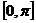 上的解为
上的解为 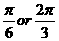 。
。
6.新教材同学做:
若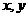 满足
满足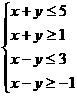 ,则目标函数
,则目标函数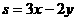 取最大值时
取最大值时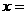
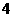 。
。
老教材同学做:
若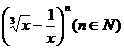 的展开式中第3项为常数项,则展开式中二项式系数最大的是第
的展开式中第3项为常数项,则展开式中二项式系数最大的是第 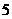 项。
项。
5.数列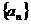 的首项为
的首项为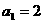 ,且
,且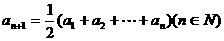 ,记
,记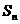 为数列
为数列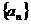 前
前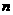 项和,则
项和,则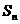
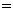
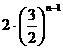 。
。
4.关于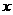 的方程
的方程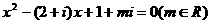 有一实根为
有一实根为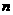 ,则
,则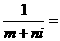
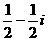 。
。
3.若角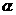 终边落在射线
终边落在射线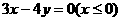 上,则
上,则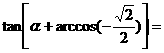
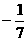 。
。
2.已知集合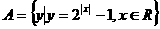 ,集合
,集合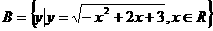 ,则集合
,则集合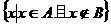
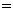
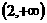 。
。
1.函数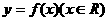 图象恒过定点
图象恒过定点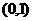 ,若
,若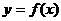 存在反函数
存在反函数 ,则
,则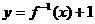 的图象必过定点
的图象必过定点 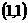 。
。
根据题目条件的特点,作出符合题意的图形(象),然后通过对图形的分析而得出正确的结论。
[例6] 设对任意实数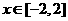 ,函数
,函数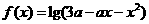 总有意义,则实数
总有意义,则实数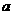 的取值范围是
。
的取值范围是
。
解:函数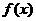 有意义,有
有意义,有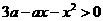 ,
,
即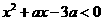 在
在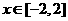 时恒成立。
时恒成立。
 设
设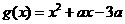 ,则当
,则当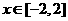 时,
时,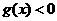 恒成立。
恒成立。
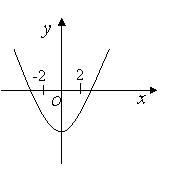
依右图抛物线的特征,有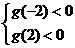 ,
,
得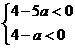 ,解得
,解得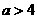 。
。
另解:函数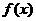 有意义,有
有意义,有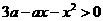 ,
,
即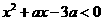 在
在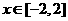 时恒成立。得
时恒成立。得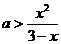 ,运用导数可求得
,运用导数可求得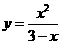
在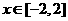 时的极大值为4,于是
时的极大值为4,于是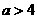 。
。
[类比1] 定义在R上的函数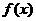 是增函数,
是增函数,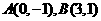 是其图象上的两点,则不等式
是其图象上的两点,则不等式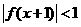 的解集为
。
的解集为
。
[类比2] 对任意实数 表示
表示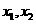 中较小的那个数,若
中较小的那个数,若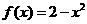 ,
,
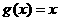 ,则
,则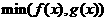 的最大值是
。
的最大值是
。
[类比3] 关于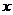 的方程
的方程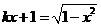 有且只有一个实根,则实数
有且只有一个实根,则实数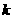 的取值范围是 。
的取值范围是 。
将需要解决的问题看作一个整体,通过研究问题的整体形式、整体结构、整体功能或作种种整体处理后,达到顺利而又简捷地解决问题的目的。
[例5] 三棱锥的三个侧面两两互相垂直,它们的侧面积分别是6、4、3,则它的体积等于 。
解:设三条棱长分别为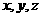 ,则
,则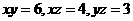 。
。
得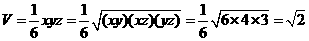 。
。
[类比1] 不等式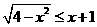 的解集为
。
的解集为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com