
题目列表(包括答案和解析)
5、若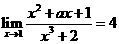 ,则 a = ( )
,则 a = ( )
A 1 B 2 C 8 D 10
4、


 已知,F1(
– 3,0) , F2 (3 , 0) 满足 PF1 –
PF2 = 2m – 1 条件的动点P的轨迹是双曲线的一支。则m可以是下列数据: ① 2; ②
– 1 ; ③ 4 ; ④ – 3 中的
已知,F1(
– 3,0) , F2 (3 , 0) 满足 PF1 –
PF2 = 2m – 1 条件的动点P的轨迹是双曲线的一支。则m可以是下列数据: ① 2; ②
– 1 ; ③ 4 ; ④ – 3 中的
A ①② B ①③ C ①②④ D ②④
3、设f (x)与g (x)是定义在R上的两个可导函数,若f (x)、g (x)满足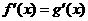 ,则f (x)与g (x)满足
,则f (x)与g (x)满足
A f (x) = g (x) B f (x) = g (x) = 0
C f (x) - g (x) 是常数函数 D f (x) +g (x)是常数函数
2、


 已知向量
已知向量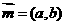 ,向量
,向量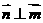 ,且
,且 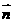 =
=  ,则
,则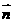 的坐标可以是
的坐标可以是
A (b,-a) B (-a,b) C (a,-b) D (-b,-a)
中,只有一项是符合题目要求的.
1、设A、B、C是三个集合,则“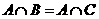 ”是“B=C”的( )
”是“B=C”的( )
A 充分但不必要条件 B 必要但不充分条件
C 充分且必要条件 D 即不充分也不必要条件
皮擦干净后,再选涂其它答案,不能答在试题卷上.
3. 考试结束,监考人员将本试卷和答题卡一并收回.
参考公式:
如果事件 、
、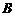 互斥,那么 球的表面积公式
互斥,那么 球的表面积公式
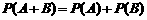 ,
, 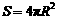
如果事件 、
、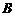 相互独立,那么 其中
相互独立,那么 其中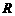 表示球的半径
表示球的半径
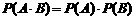 , 球的体积公式
, 球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是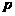 ,
, 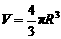
那么在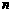 次独立重复试验中恰好发生
次独立重复试验中恰好发生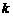 次的概率 其中
次的概率 其中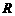 表示球的半径
表示球的半径
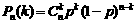 .
.
22.(本题满分18分)
已知函数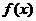 是定义在
是定义在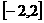 上的奇函数,当
上的奇函数,当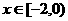 时,
时,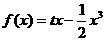 (
(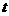 为常数)。
为常数)。
(1)求函数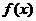 的解析式;
的解析式;
(2)当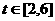 时,求
时,求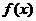 在
在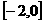 上的最小值,及取得最小值时的
上的最小值,及取得最小值时的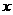 ,并猜想
,并猜想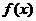 在
在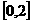 上的单调递增区间(不必证明);
上的单调递增区间(不必证明);
(3)当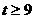 时,证明:函数
时,证明:函数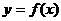 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线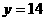 上。
上。
解:(1)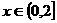 时,
时,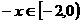 , 则
, 则 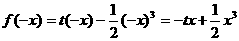
∵函数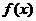 是定义在
是定义在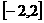 上的奇函数,即
上的奇函数,即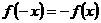
∴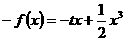 ,即
,即 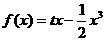 ,又可知
,又可知 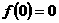
∴函数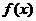 的解析式为
的解析式为 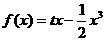 ,
,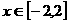
(2)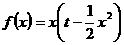 ,∵
,∵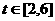 ,
,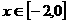 ,∴
,∴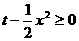
∵ 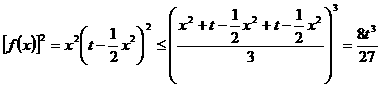
∴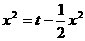 ,即
,即 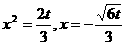
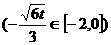 时,
时,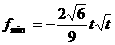 。
。
猜想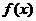 在
在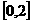 上的单调递增区间为
上的单调递增区间为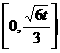 。
。
(3)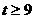 时,任取
时,任取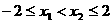 ,∵
,∵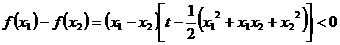
∴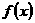 在
在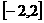 上单调递增,即
上单调递增,即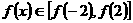 ,即
,即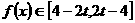
∵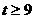 ,∴
,∴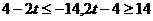 ,∴
,∴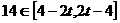
∴当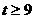 时,函数
时,函数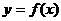 的图象上至少有一个点落在直线
的图象上至少有一个点落在直线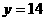 上。
上。
21.(本题满分16分)
对数列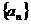 ,规定
,规定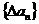 为数列
为数列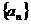 的一阶差分数列,其中
的一阶差分数列,其中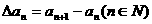 。
。
对自然数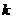 ,规定
,规定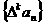 为
为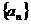 的
的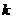 阶差分数列,其中
阶差分数列,其中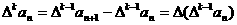 。
。
(1)已知数列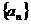 的通项公式
的通项公式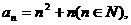 ,试判断
,试判断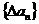 ,
,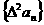 是否为等差或等比数列,为什么?
是否为等差或等比数列,为什么?
(2)若数列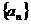 首项
首项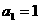 ,且满足
,且满足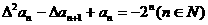 ,求数列
,求数列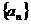 的通项公式。
的通项公式。
(3)对(2)中数列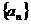 ,是否存在等差数列
,是否存在等差数列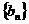 ,使得
,使得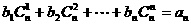 对一切自然
对一切自然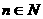 都成立?若存在,求数列
都成立?若存在,求数列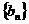 的通项公式;若不存在,则请说明理由。
的通项公式;若不存在,则请说明理由。
解:(1)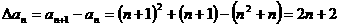 ,∴
,∴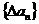 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
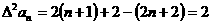
∴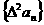 是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
是首项为2,公差为0的等差数列;也是首项为2,公比为1的等比数列。
(2)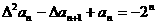 ,即
,即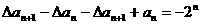 ,即
,即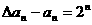 ,∴
,∴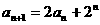
∵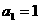 ,∴
,∴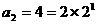 ,
,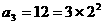 ,
,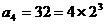 ,猜想:
,猜想: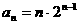
证明:ⅰ)当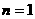 时,
时,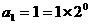 ;
;
ⅱ)假设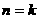 时,
时,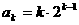
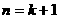 时,
时,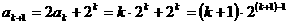 结论也成立
结论也成立
∴由ⅰ)、ⅱ)可知,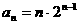
(3)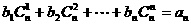 ,即
,即 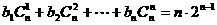
∵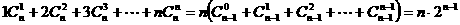
∴存在等差数列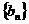 ,
,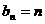 ,使得
,使得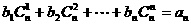 对一切自然
对一切自然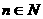 都成立。
都成立。
20.(本题满分14分)
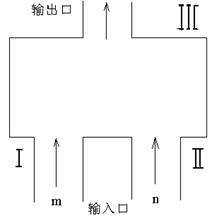 如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数
如图,一个计算装置有两个数据输入口Ⅰ、Ⅱ与一个运算结果输出口Ⅲ,当Ⅰ、Ⅱ分别输入正整数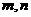 时,输出结果记为
时,输出结果记为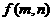 ,且计算装置运算原理如下:
,且计算装置运算原理如下:
①
若Ⅰ、Ⅱ分别输入1,则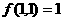 ;②若Ⅰ输入固定的正整数,
;②若Ⅰ输入固定的正整数,
Ⅱ输入的正整数增大1,则输出结果比原来增大3;③若Ⅱ输入1,
Ⅰ输入正整数增大1,则输出结果为原来3倍。
试求:
(1)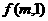 的表达式
的表达式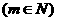 ;(2)
;(2)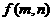 的表达式
的表达式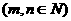 ;
;
(3)若Ⅰ、Ⅱ都输入正整数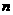 ,则输出结果
,则输出结果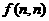 能否为2005?
能否为2005?
若能,求出相应的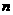 ;若不能,则请说明理由。
;若不能,则请说明理由。
解:(1)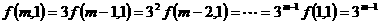
(2)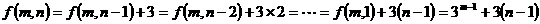
(3)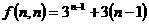 ,∵
,∵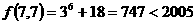 ,
,
∴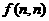 输出结果不可能为
输出结果不可能为 。
。
19.(本题满分14分)
已知关于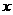 的不等式
的不等式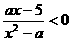 的解集为
的解集为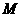 。
。
(1)当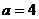 时,求集合
时,求集合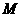 ;
;
(2)若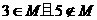 ,求实数
,求实数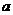 的取值范围。
的取值范围。
解:(1)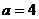 时,不等式为
时,不等式为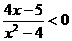 ,解之,得
,解之,得 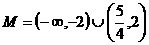
(2)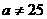 时,
时,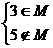
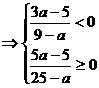
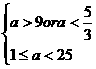
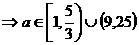
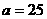 时,不等式为
时,不等式为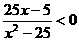 , 解之,得
, 解之,得 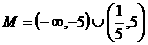 ,
,
则 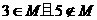 , ∴
, ∴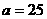 满足条件
满足条件
综上,得 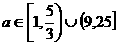 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com