
题目列表(包括答案和解析)
2.(2010辽宁理)(12) (12)有四根长都为2的直铁条,若再选两根长都为a的直铁条,使这六根铁条端点处相连能够焊接成一个三棱锥形的铁架,则a的取值范围是
(A)(0,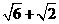 ) (B)(1,
) (B)(1,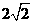 )
)
(C) (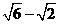 ,
,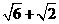 ) (D) (0,
) (D) (0,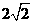 )
)
[答案]A
[命题立意]本题考查了学生的空间想象能力以及灵活运用知识解决数学问题的能力。
[解析]根据条件,四根长为2的直铁条与两根长为a的直铁条要组成三棱镜形的铁架,有以下两种情况:(1)地面是边长为2的正三角形,三条侧棱长为2,a,a,如图,此时a可以取最大值,可知AD=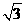 ,SD=
,SD=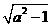 ,则有
,则有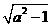 <2+
<2+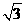 ,即
,即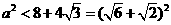 ,即有a<
,即有a<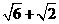
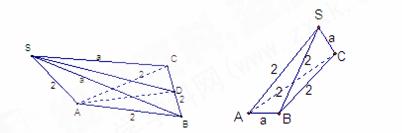
(2)构成三棱锥的两条对角线长为a,其他各边长为2,如图所示,此时a>0;
综上分析可知a∈(0,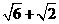 )
)
1.(2010全国卷2理)(11)与正方体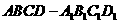 的三条棱
的三条棱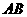 、
、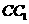 、
、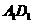 所在直线的距离相等的点
所在直线的距离相等的点
(A)有且只有1个 (B)有且只有2个
(C)有且只有3个 (D)有无数个
[答案]D
[解析]直线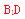 上取一点,分别作
上取一点,分别作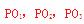 垂直于
垂直于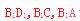 于
于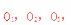 则
则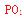

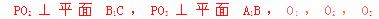 分别作
分别作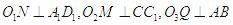 ,垂足分别为M,N,Q,连PM,PN,PQ,由三垂线定理可得,PN⊥
,垂足分别为M,N,Q,连PM,PN,PQ,由三垂线定理可得,PN⊥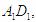 PM⊥
PM⊥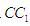 ;PQ⊥AB,由于正方体中各个表面、对等角全等,所以
;PQ⊥AB,由于正方体中各个表面、对等角全等,所以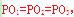
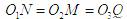 ,∴PM=PN=PQ,即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件,故选D.
,∴PM=PN=PQ,即P到三条棱AB、CC1、A1D1.所在直线的距离相等所以有无穷多点满足条件,故选D.
2010年高考题
18. (2009广东省清远一中高三综合测试)已知
(2009广东省清远一中高三综合测试)已知 中,
中,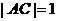 ,
,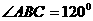 ,
,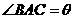 ,记
,记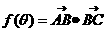 ,
,
(1)求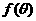 关于
关于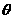 的表达式;
的表达式;
(2)求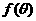 的值域;
的值域;
解(1)由正弦定理有: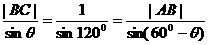 ;
;
∴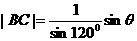 ,
,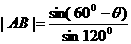 ;
;
∴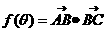

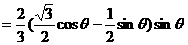
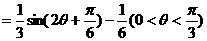
(2)由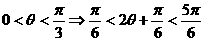 ;
;
∴ ;∴
;∴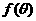
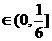
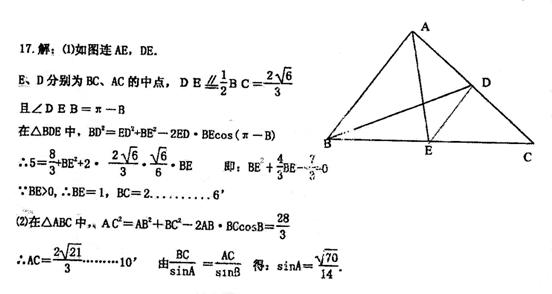
17.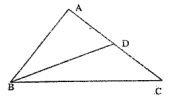 (天津市河东区2009年高三一模)如图所示,在△ABC,已知
(天津市河东区2009年高三一模)如图所示,在△ABC,已知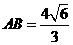 ,
,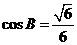 ,AC边上的中线
,AC边上的中线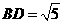 ,
,
求:(1)BC的长度;
(2) 的值。
的值。
16.(福建省泉州一中2009年高三模拟)在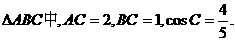
(1)求边AB的长;
(2)求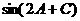 的值。
的值。
解:(1)由余弦定理,得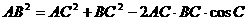
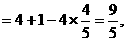
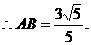
(2)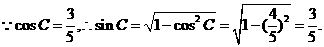
由正弦定理,得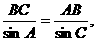
即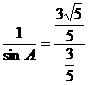 ,
,
解得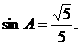
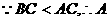 为锐角,
为锐角,
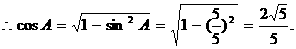
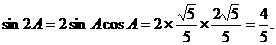
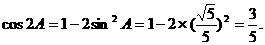
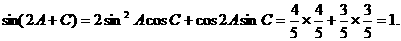
15.(安徽省合肥市一六八中学2009届高三适应性训练) 在 中,
中,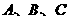 的对边
的对边
分别是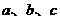 ,且满足
,且满足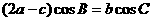 .(1)求
.(1)求 的大小;
(2)设m
的大小;
(2)设m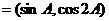 ,n
,n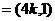
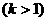 ,且m·n的最大值是5,求
,且m·n的最大值是5,求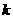 的值.
的值.
解(1)
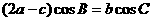 ,
, ,
,
即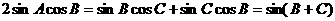
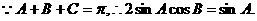
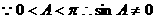 .
. 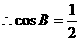 .
.
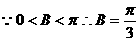
(2)m·n=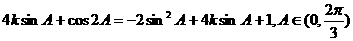 ,
,
设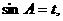 则
则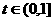 .
.
则m·n=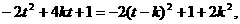
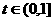
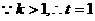 时,m·n取最大值.
时,m·n取最大值.
依题意得,(m·n) 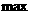 =
=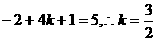
14.(天津和平区2009高三一模)在△ABC中,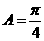 ,
,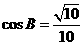 .
.
(Ⅰ)求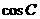 ;
;
(Ⅱ)设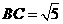 ,求
,求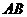 .
.
解 (Ⅰ)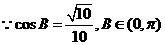

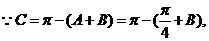
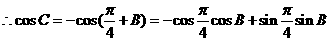
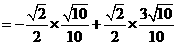
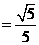
(Ⅱ)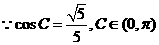
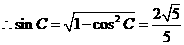 .
.
由已知条件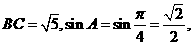
根据正弦定理,得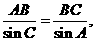
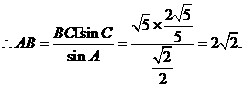
13.(山东省潍坊市2009高三一模)△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),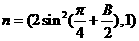 ,m⊥n,
,m⊥n,
(1)求角B的大小;
(2)若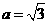 ,b=1,求c的值.
,b=1,求c的值.
解:(I) 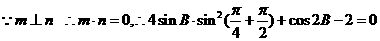 ,………2分
,………2分
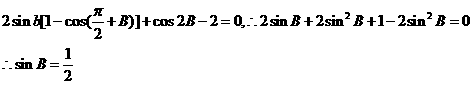

(Ⅱ) 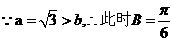
方法一:由余弦定理得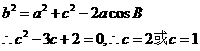
方法二:由正弦定理得
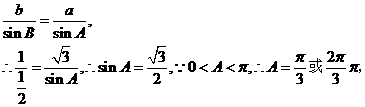
若

12.(山东省试验中学2009年高三第三次诊断性考试)在 中,
中,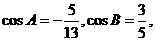
(1)求 的值
的值
(2)设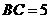 ,求
,求 的面积
的面积
.解(I)由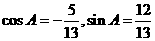 ,得
,得
由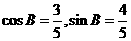 ,得
,得
又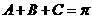
所以
(II)由正弦定理得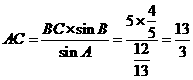
所以 的面积
的面积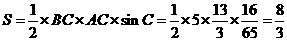
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com