
题目列表(包括答案和解析)
1.均值不等式: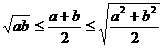
注意:①一正二定三相等;②变形,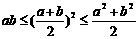 。
。
5.等差数列前n项和最值的求法:
⑴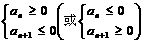 ;⑵利用二次函数的图象与性质。
;⑵利用二次函数的图象与性质。
4.前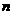 项和的求法:⑴拆、并、裂项法;⑵倒序相加法;⑶错位相减法。
项和的求法:⑴拆、并、裂项法;⑵倒序相加法;⑶错位相减法。
2.等差、等比数列性质




 等差数列
等比数列
等差数列
等比数列

 通项公式
通项公式 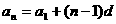
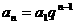
前n项和 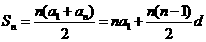
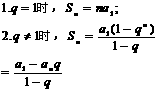
 性质 ①an=am+ (n-m)d,
①an=amqn-m;
性质 ①an=am+ (n-m)d,
①an=amqn-m;
 ②m+n=p+q时am+an=ap+aq
②m+n=p+q时aman=apaq
②m+n=p+q时am+an=ap+aq
②m+n=p+q时aman=apaq
 ③
③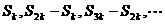 成AP ③
成AP ③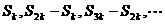 成GP
成GP

 ④
④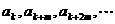 成AP,
成AP,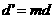 ④
④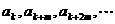 成GP,
成GP,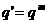
等差数列特有性质:①项数为2n时:S2n=n(an+an+1)=n(a1+a2n);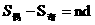 ;
;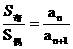 ;②项数为2n-1时:S2n-1=(2n-1)
;②项数为2n-1时:S2n-1=(2n-1)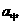 ;
;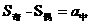 ;
;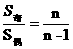 ;
;
③若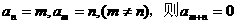 ;若
;若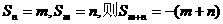 ;
;
若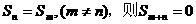 。
。
|
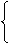
|
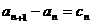 ;
;
⑷叠乘法(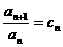 型);⑸构造法(
型);⑸构造法(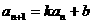 型);(6)迭代法;
型);(6)迭代法;
⑺间接法(例如: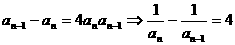 );
);
⑻作商法(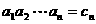 型)
型)
注:当遇到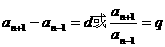 时,要分奇数项偶数项讨论,结果是分段形式。
时,要分奇数项偶数项讨论,结果是分段形式。
1.定义:
⑴等差数列 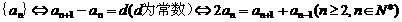
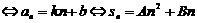 ;
;
⑵等比数列 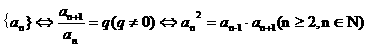
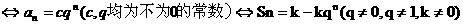 ;
;
⑴设a=(x1,y1),b=(x2,y2),则:① a∥b(b≠0) a=
a= b (
b (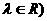
 x1y2-x2y1=0;
x1y2-x2y1=0;
② a⊥b(a、b≠0) a·b=0
a·b=0 x1x2+y1y2=0 .
x1x2+y1y2=0 .
⑵a·b=|a||b|cos<a,b>=x2+y1y2; cos<a,b>=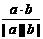 ;
;
注:①|a|cos<a,b>叫做a在b方向上的投影;|b|cos<a,b>叫做b在a方向上的投影;
② a·b的几何意义:a·b等于|a|与|b|在a方向上的投影|b|cos<a,b>的乘积。
⑶三点共线的充要条件P,A,B三点共线
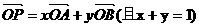 ;
;
4.求轨迹的常用方法:
(1)定义法:利用圆锥曲线的定义; (2)直接法(列等式);(3)代入法(相关点法或转移法);⑷待定系数法;(5)参数法;(6)交轨法。
3.直线与圆锥曲线问题解法:
⑴直接法(通法):联立直线与圆锥曲线方程,构造一元二次方程求解。
注意以下问题:①联立的关于“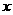 ”还是关于“
”还是关于“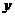 ”的一元二次方程?
”的一元二次方程?
②直线斜率不存在时考虑了吗?③判别式验证了吗?
⑵设而不求(代点相减法):--------处理弦中点问题
步骤如下:①设点A(x1,y1)、B(x2,y2);②作差得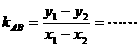 ;③解决问题。
;③解决问题。
2.结论 ⑴焦半径:①椭圆: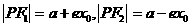 (e为离心率); (左“+”右“-”);②抛物线:
(e为离心率); (左“+”右“-”);②抛物线: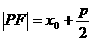
⑵弦长公式:
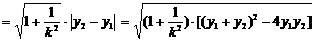 ;
;
注:(Ⅰ)焦点弦长:①椭圆: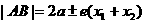 ;②抛物线:
;②抛物线: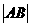 =x1+x2+p=
=x1+x2+p= ;(Ⅱ)通径(最短弦):①椭圆、双曲线:
;(Ⅱ)通径(最短弦):①椭圆、双曲线: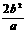 ;②抛物线:2p。
;②抛物线:2p。
⑶过两点的椭圆、双曲线标准方程可设为: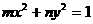 (
(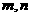 同时大于0时表示椭圆,
同时大于0时表示椭圆,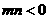 时表示双曲线);
时表示双曲线);
⑷椭圆中的结论:①内接矩形最大面积 :2ab;
②P,Q为椭圆上任意两点,且OP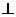 0Q,则
0Q,则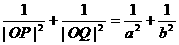 ;
;
③椭圆焦点三角形:<Ⅰ>.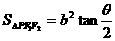 ,(
,( );<Ⅱ>.点
);<Ⅱ>.点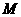 是
是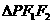 内心,
内心,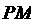 交
交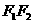 于点
于点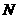 ,则
,则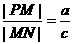 ;
;
④当点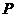 与椭圆短轴顶点重合时
与椭圆短轴顶点重合时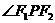 最大;
最大;
⑸双曲线中的结论:
①双曲线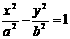 (a>0,b>0)的渐近线:
(a>0,b>0)的渐近线: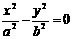 ;
;
②共渐进线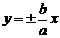 的双曲线标准方程为
的双曲线标准方程为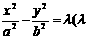 为参数,
为参数, ≠0);
≠0);
③双曲线焦点三角形:<Ⅰ>.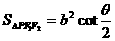 ,(
,( );<Ⅱ>.P是双曲线
);<Ⅱ>.P是双曲线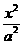 -
-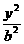 =1(a>0,b>0)的左(右)支上一点,F1、F2分别为左、右焦点,则△PF1F2的内切圆的圆心横坐标为
=1(a>0,b>0)的左(右)支上一点,F1、F2分别为左、右焦点,则△PF1F2的内切圆的圆心横坐标为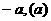 ;
;
④双曲线为等轴双曲线
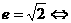 渐近线为
渐近线为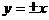
 渐近线互相垂直;
渐近线互相垂直;
(6)抛物线中的结论:
①抛物线y2=2px(p>0)的焦点弦AB性质:<Ⅰ>.
x1x2=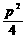 ;y1y2=-p2;
;y1y2=-p2;
<Ⅱ>.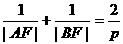 ;<Ⅲ>.以AB为直径的圆与准线相切;<Ⅳ>.以AF(或BF)为直径的圆与
;<Ⅲ>.以AB为直径的圆与准线相切;<Ⅳ>.以AF(或BF)为直径的圆与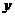 轴相切;<Ⅴ>.
轴相切;<Ⅴ>.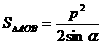 。
。
②抛物线y2=2px(p>0)内结直角三角形OAB的性质:
<Ⅰ>. 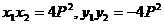 ; <Ⅱ>.
; <Ⅱ>.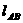 恒过定点
恒过定点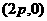 ;
;
<Ⅲ>.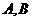 中点轨迹方程:
中点轨迹方程: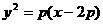 ;
;
<Ⅳ>.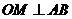 ,则
,则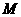 轨迹方程为:
轨迹方程为: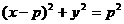 ;<Ⅴ>.
;<Ⅴ>.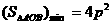 。
。
③抛物线y2=2px(p>0),对称轴上一定点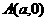 ,则:
,则:
<Ⅰ>.当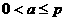 时,顶点到点A距离最小,最小值为
时,顶点到点A距离最小,最小值为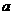 ;
;
<Ⅱ>.当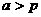 时,抛物线上有关于
时,抛物线上有关于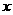 轴对称的两点到点A距离最小,最小值为
轴对称的两点到点A距离最小,最小值为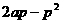 。
。
1.定义:⑴椭圆: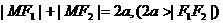 ;
;
⑵双曲线: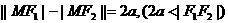 ;⑶抛物线:略
;⑶抛物线:略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com