6．空间四边形ABCD，M，N分别是AB、CD的中点，且AC＝4，BD＝6，则(　)

A．1＜MN＜5　 　　B．2＜MN＜10 　　C．1≤MN≤5　 　D．2＜MN＜5

答案：A

解析：取AD中点P，△PMN中，PM＝3，PN＝2，由三角形三边大小关系得：1＜MN＜5.故选A.

5．设a、b是异面直线，那么　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．必然存在惟一的一个平面同时平行a、b

B．必然存在惟一的一个平面同时垂直a、b

C．过a存在惟一的一个平面平行于b

D．过a存在惟一的一个平面垂直于b

答案：C

解析：A错，可以存在无数个平面同时平行于a，b.B错，不一定存在平面和a，b同时垂直．D错，过a也不一定存在平面垂直于b.综上所述C正确．

总结评述：本题考查立体几何中线面平行、垂直关系，培养学生空间想象能力．

4．(2009·山东泰安一模)设A、B、C、D是空间中四个不同的点，在下列命题中，不正确的是　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　 (　)

A．若AC与BD共面，则AD与BC共面

B．若AC与BD是异面直线，则AD与BC是异面直线

C．若AB＝AC，DB＝DC，则AD⊥BC

D．若AB＝AC，DB＝DC，则AD＝BC

答案：D

解析：若AC与BD共面，则A、B、C、D四点共面，那么AD与BC共面，所以A正确；若AC与BD是异面直线，那么A、B、C、D四点不共面，那么AD与BC是异面直线，所以B正确；若AB＝AC，DB＝DC且四点共面，显然AD⊥BC，若AB＝AC，DB＝DC且四点不共面，如图，空间四边形中，取BC中点M，连接AM、DM，显然BC⊥平面AMD，那么AD⊥BC，所以C正确．综上可知选D.

3．若点P∈α，Q∈α，R∈β，α∩β＝m，且R∉m，PQ∩m＝M，过P、Q、R三点确定一个平面γ，则β∩γ是　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．直线QR　 　　　 B．直线PR　　 C．直线RM　 　 D．以上均不正确

答案：C

解析：∵PQ∩m＝M，m⊂β，∴M∈β.

又M∈平面PQR，即M∈γ，

故M是β与γ的公共点．

又R∈β，R∈平面PQR，即R∈γ，

∴R是β与γ的公共点．∴β∩γ＝MR.

2．(2009·南京五校诊断卷)已知四个命题：(1)三点确定一个平面；(2)若点P不在平面α内，A、B、C三点都在平面α内，则P、A、B、C四点不在同一平面内；(3)两两相交的三条直线在同一平面内；(4)两组对边分别相等的四边形是平行四边形，其中正确命题的个数是(　)

A．0个　 　　　　　　 B．1个　 　　　　　　 C．2个　 　　　　　　 D．3个

答案：A

解析：根据平面的基本性质进行判断．(1)不正确，若此三点共线，则过共线的三点有无数个平面．(2)不正确，当A、B、C三点共线时，P、A、B、C四点共面．(3)不正确，共点的三条直线可能不共面，如教室墙角处两两垂直的三条直线就不共面．(4)不正确，将平行四边形沿其对角线翻折一个适当的角度后折成一个空间四边形，两组对边仍然相等，但四个点不共面，连平面图形都不是，显然不是平行四边形．故选A.

1．(教材改编题)三个平面两两相交，它们的交线条数是　　　　　　　　　　　　　　　　　 　 (　)

A．1条　B．2条　　　　 C．3条　 　 　　D．1条或3条

答案：D

解析：如图(平面图)．

16．如图，在四面体ABCD中，CB＝CD，AD⊥BD，点E、F分别是AB、BD的中点．

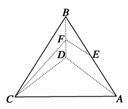
求证：

(1)直线EF∥平面ACD；

(2)平面EFC⊥平面BCD.

命题意图：本小题主要考查直线与平面、平面与平面的位置关系，考查空间想象能力、推理论证能力．

证明：(1)在△ABD中，∵E、F分别是AB、BD的中点，所以EF∥AD.

又AD⊂平面ACD，EF⊄平面ACD，∴直线EF∥平面ACD.

(2)在△ABD中，∵AD⊥BD，EF∥AD，∴EF⊥BD.

在△BCD中，∵CD＝CB，F为BD的中点，∴CF⊥BD.

∵EF⊂平面EFC，CF⊂平面EFC，EF与CF交于点F，∴BD⊥平面EFC.

又∵BD⊂平面BCD，∴平面EFC⊥平面BCD.

15．如图，l₁、l₂是互相垂直的异面直线，MN是它们的公垂线段．点A、B在l₁上，C在l₂上，AM＝MB＝MN.

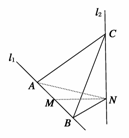
(1)求证AC⊥NB；

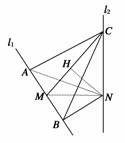(2)若∠ACB＝60°，求NB与平面ABC所成角的余弦值．

证明：(1)如图由已知l₂⊥MN，l₂⊥l₁，MN∩l₁＝M，可得l₂⊥平面ABN.

由已知MN⊥l₁，AM＝MB＝MN，可知AN＝NB且AN⊥NB.

又AN为AC在平面ABN内的射影，

∴AC⊥NB.

(2)∵Rt△CNA≌Rt△CNB，

∴AC＝BC，又已知∠ACB＝60°，因此△ABC为正三角形．

∵Rt△ANB≌Rt△CNB，

∴NC＝NA＝NB，因此N在平面ABC内的射影H是正三角形ABC的中心．连结BH，∠NBH为NB与平面ABC所成的角．

在Rt△NHB中，

cos∠NBH＝＝＝.

14．如下图，在四棱锥P－ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD＝DC.过BD作与PA平行的平面，交侧棱PC于点E，又作DF⊥PB，交PB于点F.

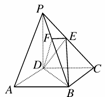
(1)求证：点E是PC的中点；

(2)求证：PB⊥平面EFD.

证明：(1)连结AC，交BD于O，则O为AC的中点，连结EO.

∵PA∥平面BDE，平面PAC∩平面BDE＝OE，∴PA∥OE.

∴点E是PC的中点；

(2)∵PD⊥底面ABCD且DC⊂底面ABCD，

∴PD⊥DC，△PDC是等腰直角三角形，而DE是斜边PC的中线，

∴DE⊥PC，①

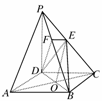又由PD⊥平面ABCD，得PD⊥BC.∵底面ABCD是正方形，CD⊥BC，∴BC⊥平面PDC.

而DE⊂平面PDC.∴BC⊥DE.②

由①和②推得DE⊥平面PBC.而PB⊂平面PBC，

∴DE⊥PB，又DF⊥PB且DE∩DF＝D，

所以PB⊥平面EFD.

13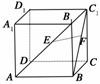．如图所示，正方体ABCD－A₁B₁C₁D₁中，侧面对角线AB₁，BC₁上分别有两点E、F，且B₁E＝C₁F，求证：EF∥ABCD.

证明：解法一：分别过E、F作EM⊥AB于M，FN⊥BC于N，连结MN.

∵BB₁⊥平面ABCD，

∴BB₁⊥AB，BB₁⊥BC，

∴EM∥BB₁，FN∥BB₁，

∴EM∥FN.

又B₁E＝C₁F，∴EM＝FN，

故四边形MNFE是平行四边形，

∴EF∥MN，

又MN在平面ABCD中，

所以EF∥平面ABCD.

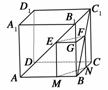
解法二：过E作EG∥AB交BB₁于G，

连结GF，则＝，

∵B₁E＝C₁F，B₁A＝C₁B，

∴＝，∴FG∥B₁C₁∥BC.

又EG∩FG＝G，AB∩BC＝B，

∴平面EFG∥平面ABCD，

而EF⊂平面EFG，

∴EF∥平面ABCD.