
题目列表(包括答案和解析)
7、(2007· 惠州)若直线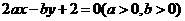 经过圆
经过圆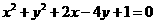 的圆心,则
的圆心,则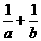 的最小值是
( )
的最小值是
( )
A.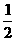 B.
B.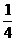 C.4 D.2
C.4 D.2
解:圆心为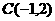 ,
,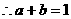 ,
,
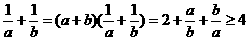
6、已知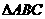 的三个顶点的坐标分别为
的三个顶点的坐标分别为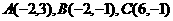 ,,以原点为圆心的圆与三角形有唯一的公共点,求圆的方程
,,以原点为圆心的圆与三角形有唯一的公共点,求圆的方程
解析:原点到三角形三边的最近距离是1,原点到三角形三个顶点的最远距离是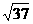 ,
,
故所求圆的方程为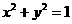 或
或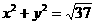
综合提高训练3-4
5、关于方程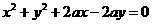 表示的圆,下列叙述中:①关于直线x+y=0对称;②其圆心在x轴上;③过原点④半径为
表示的圆,下列叙述中:①关于直线x+y=0对称;②其圆心在x轴上;③过原点④半径为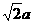 .其中叙述正确的是____(要求写出所有正确命题的序号)
.其中叙述正确的是____(要求写出所有正确命题的序号)
解析: ①③④
圆心为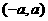 ,半径为
,半径为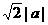 ,故①③④正确
,故①③④正确
4、直线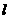 截圆
截圆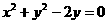 所得弦
所得弦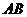 的中点是
的中点是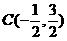 ,则
,则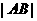 =
=
解析:圆心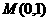 ,半径
,半径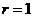 ,
,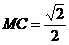 ,又
,又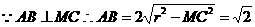
3、方程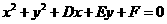 表示的圆与
表示的圆与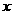 轴相切于原点,则
轴相切于原点,则
A.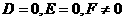 B.
B.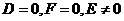
C.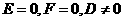 D.
D.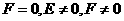
解析:圆心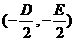 在
在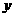 轴上,
轴上,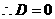 ,又圆经过原点,
,又圆经过原点,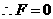
2、(2009天河区)直线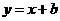 平分圆
平分圆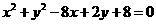 的周长,则
的周长,则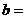
A.3 B.5 C.-3 D.-5
解析:直线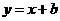 经过圆心(4,-1),
经过圆心(4,-1),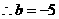
1、点(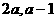 )在圆
)在圆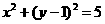 的内部,则
的内部,则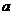 的取值范围是 ( )
的取值范围是 ( )
A.-1<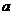 <1 B. 0<
<1 B. 0<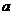 <1 C.–1<
<1 C.–1<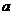 <
<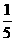 D.-
D.-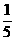 <
<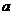 <1
<1
解析: 由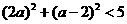 得-
得-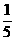 <
<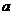 <1
<1
6.已知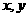 满足
满足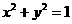 ,则
,则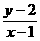 的最小值为
的最小值为
[解析] 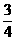
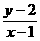 表示圆上的点
表示圆上的点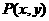 与点
与点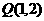 连线的斜率,所以
连线的斜率,所以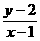 的最小值是直线
的最小值是直线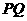 与圆相切时的斜率,
与圆相切时的斜率,
设直线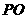 的方程为
的方程为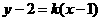 ,即
,即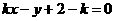
由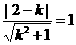 得
得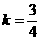 ,
,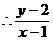 的最大值与最小值分别为
的最大值与最小值分别为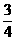
--------抢分频道★
基础巩固训练
5.已知圆的方程为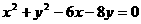 .
.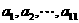 是该圆过点(3,5)的11条弦的长,若数列
是该圆过点(3,5)的11条弦的长,若数列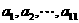 是等差数列,则 数列
是等差数列,则 数列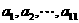 的公差的最大值为
的公差的最大值为
[解析] 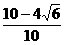
圆心坐标为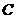 (3,4),半径为5,圆的弦长的最小值和最大值分别是
(3,4),半径为5,圆的弦长的最小值和最大值分别是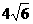 和10,
和10,
数列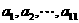 的公差的最大值为
的公差的最大值为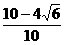
考点: 与圆有关的最值
题型:求与圆有关的最值
[例4 ]已知圆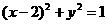 ,求(1)
,求(1)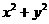 的最大值(2)
的最大值(2)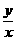 的最大值与最小值(3)
的最大值与最小值(3)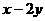 的最小值
的最小值
[解题思路]根据所求式子的几何意义求解或转化为函数的最值
[解析](1)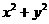 表示圆上的点
表示圆上的点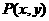 到原点的距离的平方
到原点的距离的平方
因圆心到点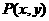 的距离为2,
的距离为2,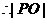 的最大值为3,从而
的最大值为3,从而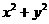 的最大值为9
的最大值为9
方法2:设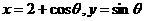 ,则
,则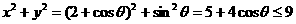
(2)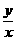 表示圆上的点
表示圆上的点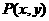 与原点连线的斜率,所以
与原点连线的斜率,所以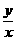 的最大值与最小值是直线
的最大值与最小值是直线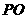 与圆相切时的斜率,
与圆相切时的斜率,
设直线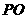 的方程为
的方程为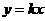 ,
,
由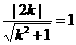 得
得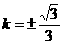 ,
,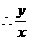 的最大值与最小值分别为
的最大值与最小值分别为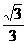 和
和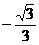
(3)设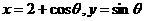 ,
,
则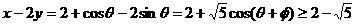
解法2:设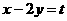 ,则
,则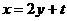 ,
,
代入圆的方程并化简得: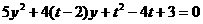
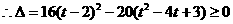 ,解得:
,解得: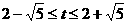
[名师指引](1)与圆有关的最值的求法有:几何法、函数法、判别式法
(2)用几何法时,要见“数”想“形”,即所求式子的几何意义
(3)用函数法时,常用三角换元
[新题导练]
4.动点P到点A(8,0)的距离是到点B(2,0)的距离的2倍,那么点的轨迹方程为( )
A. 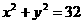 B.
B. 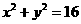 C.
C. 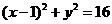 D.
D. 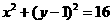
[解析]B
设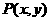 ,则
,则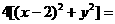
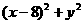 ,化简得
,化简得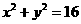
考点2 圆的几何性质
题型1:运用圆的几何性质解题
[例3 ]一圆与y轴相切,圆心在直线x-3y=0上,且直线y=x截圆所得弦长为2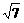 ,求此圆的方程.
,求此圆的方程.
[解题思路]因题目条件与圆心、半径关系密切,选择圆的标准方程,与弦长有关的问题,一般要利用弦心距、半径、半弦长构成的“特征三角形”
[解析]:因圆与y轴相切,且圆心在直线x-3y=0上,故设圆方程为
(x-3b)2+(y-b)2=9b2.
又因为直线y=x截圆得弦长为2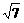 ,
,
则有(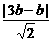 )2+(
)2+(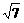 )2=9b2,
)2=9b2,
解得b=±1.故所求圆方程为
(x-3)2+(y-1)2=9或(x+3)2+(y+1)2=9.
[名师指引]在求圆的方程时,应当注意以下几点:
(1)确定用圆的标准方程还是一般方程;
(2)运用圆的几何性质(如本例的相切、弦长等)建立方程求得a、b、r或D、E、F;
(3)在待定系数法的应用上,列式要尽量减少未知量的个数.
[例4 ] 已知⊙O的半径为3,直线l与⊙O相切,一动圆与l相切,并与⊙O相交的公共弦恰为⊙O的直径,求动圆圆心的轨迹方程.
[解题思路]问题中的几何性质十分突出,如何利用切线、直径、垂直、圆心这些几何性质是关键,动圆圆心满足的条件是关注的焦点
[解析]取过O点且与l平行的直线为x轴,过O点且垂直于l的直线为y轴,建立直角坐标系.
设动圆圆心为M(x,y),
⊙O与⊙M的公共弦为AB,⊙M与l切于点C,则|MA|=|MC|.
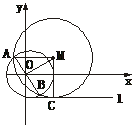
∵AB为⊙O的直径,
∴MO垂直平分AB于O.
由勾股定理得|MA|2=|MO|2+|AO|2=x2+y2+9,而|MC|=|y+3|,
∴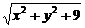 =|y+3|.
=|y+3|.
化简得x2=6y,这就是动圆圆心的轨迹方程.
[名师指引]求轨迹的步骤是“建系,设点,列式,化简”,建系的原则是特殊化(把图形放在最特殊的位置上),这类问题一般需要通过对图形的观察、分析、转化,找出一个关于动点的等量关系。
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com