12．P为△ABC所在平面外一点，PA、PB、PC与平面ABC所成角均相等，又PA与BC垂直，那么△ABC形状可以是________．

①正三角形　②等腰三角形　③非等腰三角形　④等腰直角三角形(将你认为正确的序号全填上)

答案：①②④

解析：设点P在底面ABC上的射影为O，由PA、PB、PC与平面ABC所成角均相等，得OA＝OB＝OC，即点O为△ABC的外心，又由PA⊥BC，得OA⊥BC，即AO为△ABC中BC边上的高线，∴AB＝AC，即△ABC必为等腰三角形，故应填①②④.

11．对于四面体ABCD，给出下列四个命题：

①若AB＝AC，BD＝CD，则BC⊥AD；

②若AB＝CD，AC＝BD，则BC⊥AD；

③若AB⊥AC，BD⊥CD，则BC⊥AD；

④若AB⊥CD，AC⊥BD，则BC⊥AD.

其中真命题的序号是________．(把你认为是正确命题的序号都填上)

答案：①④

解析：本题考查四面体的性质，取BC的中点E，则BC⊥AE，BC⊥DE，∴BC⊥面ADE，∴BC⊥AD，故①正确．设O为A在面BCD上的射影，依题意OB⊥CD，OC⊥BD，∴O为垂心，∴OD⊥BC，∴BC⊥AD，故④正确，②③易排除，故答案为①④.

10．如下图所示，PA⊥矩形ABCD所在的平面，那么以P、A、B、C、D五个点中的三点为顶点的直角三角形的个数是________．

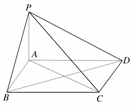
答案：9个

解析：C－1＝10－1＝9，(包括△PBD，为什么说△PBD不为Rt△)

易判断∠PDB≠90°.

∠PBD≠90°，只须判断∠BPD≠90°.

假设∠BPD＝90°，设PA＝a，AD＝b，AB＝c.

∴PB²＝a²+c²，PD²＝a²+b²

∵∠BPD＝90°，∴BD²＝b²+c²+2a²

而由Rt△ABD得：BD²＝b²+c².

这显然不成立．∴∠BPD≠90°.

综合而得：△PBD不是Rt△，Rt△共有9个．

9．过三棱柱ABC-A₁B₁C₁任意两条棱的中点作直线，其中与平面ABB₁A₁平行的直线共有________条．

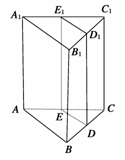
答案：6

解析：如图，过任意两条棱中点的直线与平面ABB₁A₁平行的直线有：DE、DD₁、DE₁、D₁E₁、D₁E、EE₁共6条．

8．在一个45°的二面角的一平面内有一条直线与二面角的棱成45°角，则此直线与二面角的另一个面所成的角为(　)

A．30°　 　　　　　　　　　　 B．45°　 　　　　　　　 C．60°　 　　　　　　　 D．90°

答案：A

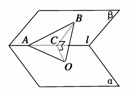解析：解法一：由于45°的二面角的一平面内一条直线与二面角的棱成45°角，根据最小角定理，则此直线为二面角的另一个面所成的角小于45°，故选A.

解法二：如图，α-l-β成45°角，∠BAC＝45°，∠BCO＝45°为二面角的平面角，BO⊥α，设OB＝OC＝1，则BC＝，AO＝.tan∠BAO＝＝，∠BAO＝30°.

故选A.

7．下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得到AB∥平面MNP的图形的序号是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

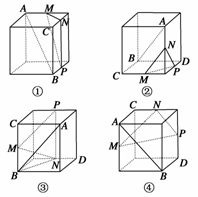
A.①、③　 　　　　　　　　　　　　　　　　　　　 B．②、③

C．①、④　 　　　　　　　　　　　　　　　　　　 D．②、④

答案：C

解析：如①图中，连结AC，则平面ACB∥平面MNP，又AB⊂面ACB，∴AB∥面MNP；

如②图中，平面ACD∥平面MNP，又AB与面ACD相交，所以AB与面MNP也相交；

如③图中，因为AB与平面NPCB相交，所以AB与平面MNP相交；

如④图中，AB∥CD，CD∥NP，那么AB∥NP，AB∥平面MNP.

综上所述，正确答案为①、④.故选C.

6．(2009·鄞州中学试题)已知a，b是异面直线，a⊥平面M，b⊥平面N，则平面M，N的位置关系是　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．相交　 　　　　　　 B．平行　 　　　　　　 C．垂直　 　　　　　　 D．不能确定

答案：A

解析：如果M∥N，则必有a∥b，故平面M，N必相交，故应选A.

5．给定空间中的直线l及平面α，条件“直线l与平面α内无数条直线都垂直”是“直线l与平面α垂直”的　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．充要条件　　　　　　 B．充分非必要条件

C．必要非充分条件　　　 D．既非充分又非必要条件

答案：C

解析：当l与平面α内无数条直线都垂直时，l与α不一定垂直，故不充分．

当l⊥α时，l一定垂直于α内无数条直线，故必要．

4．一条直线l上有相异三个点A、B、C到平面α的距离相等，那么直线l与平面α的位置关系是　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．l∥α　B．l⊥α 　　　C．l与α相交但不垂直　　 D．l∥α或l⊂α

答案：D

解析：l∥α时，直线l上任意点到α的距离都相等；l⊂α时，直线l上的所有点与α距离都是0；l⊥α时，直线l上只能有两点到α距离相等；l与α斜交时，也只能有两点到α距离相等．

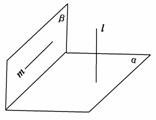
3．(2009·河北秦皇岛一模)已知直线l⊥平面α，直线m⊂平面β，下面有三个命题①α∥β⇒l⊥m；②α⊥β⇒l∥m；③l∥m⇒α⊥β.则真命题的个数为　　　　　　　　　　　　　　　　　　　 (　)

A．0　　B．1　　C．2　　D．3

答案：C

解析：①正确；②不正确，如图，直线l与m可能异面；③正确，是面与面垂直的判定定理．故选C.