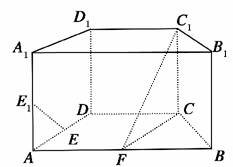
16．(2009·山东，18)如图所示，在直四棱柱ABCD－A₁B₁C₁D₁中，底面ABCD为等腰梯形，AB∥CD，AB＝4，BC＝CD＝2，AA₁＝2，E、E₁、F分别是棱AD、AA₁、AB的中点．

(1)证明：直线EE₁∥平面FCC₁；

(2)求二面角B－FC₁－C的余弦值．

解析：(1)证法一：取A₁B₁的中点F₁，连结FF₁、C₁F₁，

由于FF₁∥BB₁∥CC₁，

所以F₁∈平面FCC₁，

因此平面FCC₁即为平面C₁CFF₁，

连结A₁D、F₁C，由于A₁F₁綊D₁C₁綊CD，

所以四边形A₁DCF₁为平行四边形，因此A₁D∥F₁C.

又EE₁∥A₁D，得EE₁∥FC，

而EE₁⊄平面FCC₁，F₁C⊂平面FCC₁，

故EE₁∥平面FCC₁.

证法二：因为F为AB的中点，CD＝2，AB＝4，

AB∥CD，所以CD綊AF，

因此四边形AFCD为平行四边形，所以AD∥FC.

又CC₁∥DD₁，FC∩CC₁＝C，

FC⊂平面FCC₁，CC₁⊂平面FCC₁，

所以平面ADD₁A₁∥平面FCC₁，

又EE₁⊂平面ADD₁A₁，

所以EE₁∥平面FCC₁.

(2)解法一：取FC的中点H，

由于FC＝BC＝FB，所以BH⊥FC.

又BH⊥CC₁，所以BH⊥平面FCC₁.

过H作HG⊥C₁F于G，连结BG.

由于HG⊥C₁F，BH⊥平面FCC₁，所以C₁F⊥平面BHG，

因此BG⊥C₁F，所以∠BGH为所求二面角的平面角．

在Rt△BHG中，BH＝，

又FH＝1，且△FCC₁为等腰直角三角形，

所以HG＝，BG＝＝，

因此cos∠BGH＝＝＝，

即所求二面角的余弦值为.

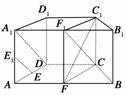
解法二：过D作DR⊥CD交AB于R，以D为坐标原点建立如图所示的空间直角坐标系，

则F(，1,0)，B(，3,0)，C(0,2,0)，C₁(0,2,2)，

所以＝(0,2,0)，＝(－，－1,2)，＝(，3,0)，

由FB＝CB＝CD＝DF，所以DB⊥FC.

又CC₁⊥平面ABCD，所以为平面FCC₁的一个法向量．

设平面BFC₁的一个法向量为n＝(x，y，z)，

则由，得

即

取x＝1，得

因此n＝(1,0，)，

所以cos〈，n〉＝

＝＝＝.

故所求二面角的余弦值为.

15．如图，四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD＝PD，E、F分别为CD、PB的中点．

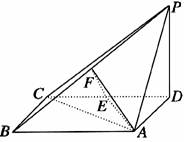
(1)求证：EF⊥平面PAB；

(2)设AB＝BC，求AC与平面AEF所成的角的大小．

解析：解法一：(1)证明：连结EP，

∵PD⊥底面ABCD，DE在平面ABCD内，∴PD⊥DE.又CE＝ED，PD＝AD＝BC.

∴Rt△BCE≌Rt△PDE.∴PE＝BE.

∵F为PB中点，∴EF⊥PB.

由三垂线定理得PA⊥AB，

∴在Rt△PAB中PF＝AF.又PE＝BE＝EA，

∴△EFP≌△EFA.∴EF⊥FA.

∵PB、FA为平面PAB内的相交直线，∴EF⊥平面PAB.

(2)解：不妨设BC＝1，则AD＝PD＝1，

AB＝，PA＝，AC＝.

∴△PAB为等腰直角三角形，且PB＝2，

F为其斜边中点，BF＝1，且AF⊥PB.

∵PB与平面AEF内两条相交直线EF、AF都垂直，

∴PB⊥平面AEF.

连结BE交AC于G，作GH∥BP交EF于H，则GH⊥平面AEF，∠GAH为AC与平面AEF所成的角．

由△EGC∽△BGA，可知EG＝GB，EG＝EB，

AG＝AC＝.由△EGH∽△EBF，

可知GH＝BF＝.

∴sin∠GAH＝＝.

∴AC与平面AEF所成的角为arcsin.

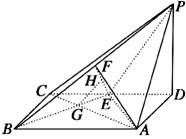
解法二：以D为坐标原点，DA的长为单位长，建立如图所示的直角坐标系．

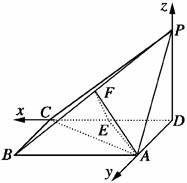
(1)证明：设E(a,0,0)，其中a>0，则C(2a,0,0)，A，(0,1,0)，B(2a,1,0)，P(0,0,1)，F(a，，)，

＝(0，，)，＝(2a,1，－1)，＝(2a,0,0)．

∵·＝0，∴EF⊥PB.

∵·＝0，∴EF⊥AB.

又PB⊂平面PAB，AB⊂平面PAB，PB∩AB＝B，

∴EF⊥平面PAB.

(2)解：由AB＝BC，得a＝.

可得＝(，－1,0)，＝(，1，－1)，

cos〈，〉＝＝，

异面直线AC、PB所成的角为arccos.

＝(，－，)，∴·＝0，PB⊥AF.

又PB⊥EF，EF、AF为平面AEF内两条相交直线，

∴PB⊥平面AEF.

AC与平面AEF所成的角为－arccos，即arcsin.

14．如图，PD垂直正方形ABCD所在的平面，AB＝2，E是PB的中点，cos〈，〉＝.

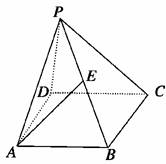
(1)建立适当的空间坐标系，写出点E的坐标；

(2)在平面PAD内求一点F，使EF⊥平面PCB.

解析：(1)以DA、DC、DP所在直线分别为x轴、y轴、z轴建立空间坐标系，如图，得到坐标：

A(2,0,0)，B(2,2,0)，C(0,2,0)，设P(0,0,2m)⇒E(1,1，m)，

∴＝(－1,1，m)，＝(0,0,2m)，

∴cos〈，〉＝＝⇒m＝1，

∴点E的坐标是(1,1,1)．

(2)∵F∈平面PAD，∴可设F(x,0，z)⇒

＝(x－1，－1，z－1)，

∵EF⊥平面PCB，

∴⊥⇒(x－1，－1，z－1)·(2,0,0)＝0⇒x＝1，

∵⊥，

∴⊥⇒(x－1，－1，z－1)·(0,2，－2)＝0⇒z＝0.

∴点F的坐标是(1,0,0)，即点F是AD的中点．

13．(2009·杭州名校联测)如图，正三棱锥P－ABC，PA＝4，AB＝2，D为BC中点，点E在AP上，满足AE＝3EP.

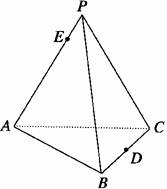
(1)建立适当坐标系，写出A、B、D、E四点的坐标；

(2)求异面直线AD与BE所成的角．

解析：(1)建立如图坐标系：O为△ABC的重心，直线OP为z轴，AD为y轴，x轴平行于CB，得A(0，－，0)、B(1，，0)、D(0，，0)、E(0，－，)．

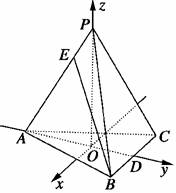
(2)＝(0，，0)，＝(－1，－，)．设AD与BE所成的角为θ，则

cosθ＝＝＝.

∴θ＝arccos.

12．设a，b是直线，α，β是平面，a⊥α，b⊥β，向量a₁在a上，向量b₁在b上，a₁＝(1,1,1)，b₁＝(－3,4,0)，则α，β所成二面角中较小的一个为________．

答案：arccos

解析：由cos?a₁·b₁?＝＝

＝＝，

所以α，β所成二面角中较小的一个为arccos.

11．(2009·台湾，11)如图所示，正方体ABCD－EFGH的棱长等于2(即|A|＝2)，K为正方形ABCD的中心，M、N分别为线段BF、EF的中点．试问下列选项是正确的序号为________．

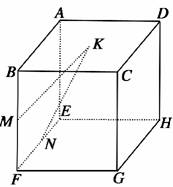
(1)＝－+；

(2)·＝1；

(3)＝3；

(4)△KMN为一直角三角形；

(5)△KMN的面积为10.

答案：(1)(4)

解析：如图，建立空间直角坐标系E－xyz.

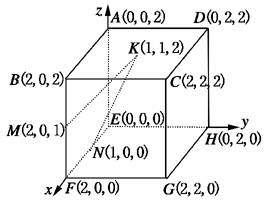
∵＝(1，－1，－1，)，－+＝(2,0,0)－(0,2,0)+(0,0，－2)＝(1，－1，－1)，

∴＝－+，

∴·＝(1，－1，－1)·(2,0,0)＝2≠1.

∵＝(1，－1，－1)，∴||＝≠3.

∵||＝，||＝，||＝⇒||²＝||²+||²，

∴△KMN为直角三角形，

∴△KMN的面积为＝≠10.

故选(1)(4)．

10．(2009·安徽，11)在空间直角坐标系中，已知点A(1,0,2)，B(1，－3,1)，点M在y轴上，且M到A与到B的距离相等，则M的坐标是________．

答案：(0，－1,0)

解析：设M(0，y,0)，由|MA|＝|MB|得

(1－0)²+(0－y)²+(2－0)²＝(1－0)²+(－3－y)²+(1－0)²，解得y＝－1.

∴M(0，－1,0)．

9．在空间直角坐标系O－xyz中，给定点P(2，－1,3)，若点A与点P关于xOy平面对称，点B与点P关于z轴对称，则|AB|＝________.

答案：2

解析：依题意，得知

A(2，－1，－3)，B(－2,1,3)，则＝(－4,2,6)，|AB|＝＝＝2.

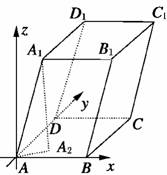
8．平行六面体ABCD－A₁B₁C₁D₁中，AB＝1，AD＝2，AA₁＝3，∠BAD＝90°，∠BAA₁＝∠DAA₁＝60°，则对角线A₁C的长为(　)

A.　 B.

C.　 D.

答案：C

解析：由题意建立如图坐标系，

作A₁A₂⊥平面xAy，

由cos∠DAA₁＝cos∠A₁AA₂·cos∠DAA₂，即cos60°＝cos45°·cos∠A₁AA₂，

得cos∠A₁AA₂＝.

分析可得A₁(，，)，C(1,2,0)

∴A₁C＝＝，故选C.

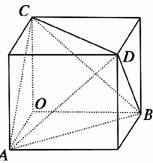
7．(2009·江西，9)如图所示，正四面体ABCD的顶点A，B，C分别在两两垂直的三条射线Ox，Oy，Oz上，则在下列命题中，错误的为　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．O－ABC是正三棱锥

B．直线OB∥平面ACD

C．直线AD与OB所成的角是45°

D．二面角D－OB－A的为45°

答案：B

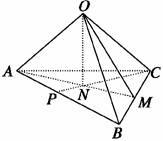解析：①如图，ABCD为正四面体，

∴△ABC为等边三角形，

又∵OA、OB、OC两两垂直．

∴OA⊥面OBC，∴OA⊥BC，

过O作底面ABC的垂线，垂足为N，

连结AN交BC于M，

由三垂线定理可知BC⊥AM，

∴M为BC的中点，

同理可证，连结CN交AC于P，则P为AB中点，∴N为底面△ABC中心，

∴O－ABC是正三棱锥，故A正确．

②将正四面体ABCD放入正方体中，如图所示，显然OB与面ACD不平行，故选B.