
题目列表(包括答案和解析)
1.借助空间几何模型进行想象,理解空间点的位置关系及坐标关系
问题1:点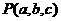 到
到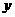 轴的距离为
轴的距离为
[解析]借助长方体来思考,以点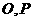 为长方体对角线的两个顶点,点
为长方体对角线的两个顶点,点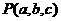 到
到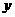 轴的距离为长方体一条面对角线的长度,其值为
轴的距离为长方体一条面对角线的长度,其值为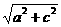
5.以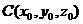 为球心,
为球心, 为半径的球面方程为
为半径的球面方程为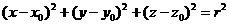
特殊地,以原点为球心, 为半径的球面方程为
为半径的球面方程为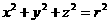
★重难点突破★
重点:了解空间直角坐标系,会用空间直角坐标系表示点的位置,会推导和使用空间两点间的距离公式
难点:借助空间想象和通过与平面直角坐标系的类比,认识空间点的对称及坐标间的关系
重难点: 在空间直角坐标系中,点的位置关系及空间两点间的距离公式的使用
5.空间两点间的距离公式
已知空间两点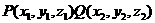 ,
,
则两点的距离为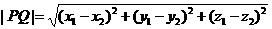 ,
,
特殊地,点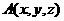 到原点
到原点 的距离为
的距离为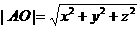 ;
;
4. 已知空间两点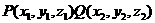 ,则线段
,则线段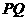 的中点坐标为
的中点坐标为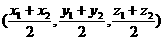
3、点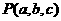 关于
关于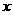 轴的对称点的坐标为
轴的对称点的坐标为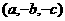
点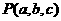 关于
关于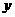 轴的对称点的坐标为
轴的对称点的坐标为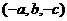 ;
;
点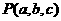 关于
关于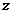 轴的对称点的坐标为
轴的对称点的坐标为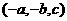 ;
;
点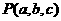 关于坐标平面
关于坐标平面 的对称点为
的对称点为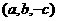 ;
;
点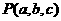 关于坐标平面
关于坐标平面 的对称点为
的对称点为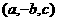 ;
;
点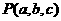 关于坐标平面
关于坐标平面 的对称点为
的对称点为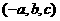 ;
;
点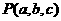 关于原点的对称点
关于原点的对称点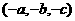 。
。
2、在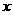 轴上的点分别可以表示为
轴上的点分别可以表示为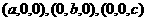 ,
,
在坐标平面 ,
, ,
, 内的点分别可以表示为
内的点分别可以表示为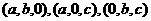 ;
;
1.右手直角坐标系
①右手直角坐标系的建立规则: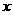 轴、
轴、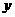 轴、
轴、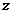 轴互相垂直,分别指向右手的拇指、食指、中指;
轴互相垂直,分别指向右手的拇指、食指、中指;
②已知点的坐标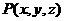 作点的方法与步骤(路径法):
作点的方法与步骤(路径法):
沿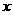 轴正方向(
轴正方向(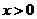 时)或负方向(
时)或负方向(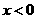 时)移动
时)移动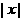 个单位,再沿
个单位,再沿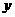 轴正方向(
轴正方向(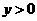 时)或负方向(
时)或负方向(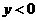 时)移动
时)移动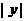 个单位,最后沿
个单位,最后沿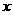 轴正方向(
轴正方向(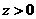 时)或负方向(
时)或负方向(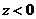 时)移动
时)移动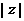 个单位,即可作出点
个单位,即可作出点
③已知点的位置求坐标的方法:
过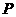 作三个平面分别与
作三个平面分别与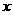 轴、
轴、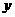 轴、
轴、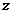 轴垂直于
轴垂直于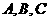 ,点
,点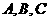 在
在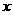 轴、
轴、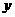 轴、
轴、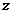 轴的坐标分别是
轴的坐标分别是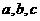 ,则
,则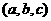 就是点
就是点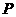 的坐标
的坐标
9.数列 中,
中,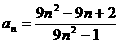 .
.
⑴求这个数列的第10项;
⑵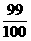 是否为该数列的项,为什么?
是否为该数列的项,为什么?
⑶求证: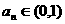 ;
;
⑷在区间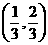 内有无数列的项,若有,有几项?若无,说明理由.
内有无数列的项,若有,有几项?若无,说明理由.
[解析]⑴
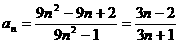 ,
,
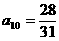 ;
;
⑵令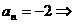
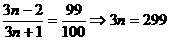 ,无整数解,
,无整数解,
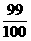 不是该数列的项.
不是该数列的项.
⑶
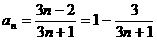 ,
,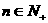 ,
,
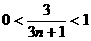 ,
,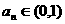
⑷由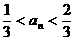 ,得
,得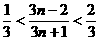

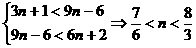 ,
, 当且仅当
当且仅当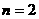 时,在区间
时,在区间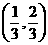 内有数列的项.
内有数列的项.
8.设数列 的第
的第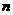 项
项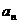 是二次函数,
是二次函数,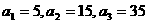 ,求
,求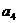 .
.
[解析]设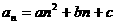 ,由
,由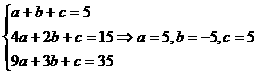

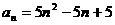 ,
,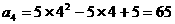 .
.
7.(2009恩城中学 节选)已知数列
节选)已知数列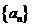 的首项
的首项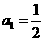 ,其前
,其前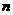 项和
项和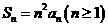 .求数列
.求数列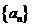 的通项公式.
的通项公式.
[解析]由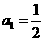 ,
,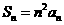 ,① ∴
,① ∴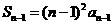 ,②
,②
①-②得: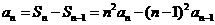 ,即,
,即,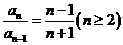 ,
,
∵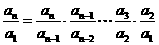
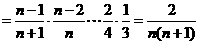 ,∴
,∴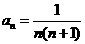 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com