7．下图(a)，在直角梯形ABCD中，∠B＝90°，DC∥AB，动点P从B点出发，由B?C?D?A沿边运动，设点P运动的路程为x，△ABP的面积为y，如果关于x的函数y的图象如下图(b)，则△ABC的面积等于　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　 (　)

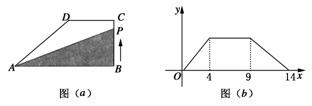
A．10　 　　　　 B．16 　　　　　　　　 C．18　 　　　　 D．32

答案：B

解析：由题可知，BC＝4，CD＝5，AD＝5，∴AB＝3+5＝8，∴S_△ABC＝×8×4＝16，故选B.

6．设y＝f(x)的定义域为A＝[4，+∞)．给出下列函数：y＝f(2x－4)，y＝f()，y＝f(2)，y＝f(－)，其中定义域仍是A的有　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1个　 　　　 B．2个　 　　　　　　 C．3个　 　　　 D．4个

答案：B

解析：∵2x－4≥4，∴x≥4，因此y＝f(2x－4)定义域仍为A.同理可知y＝f(2)定义域仍为A.故选B.

5．(2009·重庆市高三联合诊断性考试(第一次))已知函数f(x)＝，则f[f()]的值是　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－　 　　　 B．－9 　　　　　　　 C.　 　　　　　　 D．9

答案：C

解析：依题意得f()＝log₂＝－2，f[f()]＝f(－2)＝3^－2＝，选C.

4．(2010·湖北省大冶实验中学月考)函数f(x)是偶函数，当x>0时，f(x)＝1+2x－x²，当x<0时，f(x)＝　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．1+2x－x²　 　　　　　　　　　　　　 B．1－2x－x²

C．1+2x+x²　 　　　　　　　　　　　　 D．1－2x+x²

答案：B

解析：当x<0时，f(x)＝f(－x)＝1+2(－x)－(－x)²＝1－2x－x²，故选B.

3．(2009·山东，7)定义在R上的函数f(x)满足f(x)＝则f(3)的值为　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A．－1　　B．－2　　　　 C．1　　　 D．2

答案：B

解析：∵x＞0时，f(x)＝f(x－1)－f(x－2)，

∴f(3)＝f(2)－f(1)＝f(1)－f(0)－f(1)＝－f(0)＝－log₂(4－0)＝－2.故选B.

2．(2009·湖北省八校高三第一次联考)设f(x)＝，则f()+f()+f(－2)+f(－3)＝　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　)

A.　　　 B．－　　　　 C．1　　　 D．0

答案：D

解析：∵f(x)＝，∴f()＝，f(－2)＝－，f()＝，f(－3)＝－.∴f()+f()+f(－2)+f(－3)＝0，故选D.

1．(2009·江西，2)函数y＝的定义域为　　　　　　　　　　　　　　　　　　　　 (　)

A．[－4,1]　　　　 B．[－4,0)

C．(0,1]　 　　　　　　　　　　　　　 D．[－4,0)∪(0,1]

答案：D

解析：求y＝的定义域．

即⇒x∈[－4,0)∪(0,1]．

16．(2009·江苏南通中学模拟)设函数f(x)＝|2x+1|－|x－4|.

(1)求函数f(x)的值域；

(2)若关于x的不等式f(x)≥a²－3a－7在[0,5]上恒成立，试求a的取值范围．

解析：(1)f(x)＝，作出其图象(如下图)，

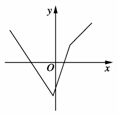
所以，函数f(x)的值域是[－，+∞)．

(2)由图象可知，函数f(x)在[0,5]上的最小值为f(0)＝－3，由题意可知，f(0)≥a²－3a－7，因此－1≤a≤4.

15．在经济学中，函数f(x)的边际函数Mf(x)定义为Mf(x)＝f(x+1)－f(x)．某公司每月最多生产100台报警系统装置，生产x(x＞0)台的收入函数为R(x)＝3000x－20x²(单位：元)，其成本函数为C(x)＝500x+4000(单位：元)，利润是收入与成本之差．

(1)求利润函数P(x)及边际利润函数MP(x)；

(2)利润函数P(x)与边际利润函数MP(x)是否具有相同的最大值？

解析：(1)P(x)＝R(x)－C(x)

＝(3000x－20x²)－(500x+4000)

＝－20x²+2500x－4000(x∈[1,100]且x∈N)．

MP(x)＝P(x+1)－P(x)

＝－20(x+1)²+2500(x+1)－4000－(－20x²+2500x－4000)＝2480－40x(x∈[1,100]且x∈N)．

(2)P(x)＝－20(x－)²+74125，

当x＝62或63时，P(x)_max＝74120(元)．

因为MP(x)＝2480－40x是减函数，

所以当x＝1时，MP(x)_max＝2440(元)．

因此，利润函数P(x)与边际利润函数MP(x)不具有相同的最大值．

14．(1)若函数y＝lg(x²－ax+9)的定义域为R，求a的范围及函数值域；

(2)若函数y＝lg(x²－ax+9)的值域为R，求a的取值范围及定义域．

解析：(1)函数的定义域为R.

即x²－ax+9>0恒成立，

则△＝a²－36<0恒成立，所以－6<a<6.

此时，x²－ax+9＝(x－)²+9－≥9－，

∴a的范围是(－6,6)，值域为[lg(9－)，+∞)．

(2)函数的值域为R，

即真数x²－ax+9必能取遍所有正数，二次函数g(x)＝x²－ax+9的图象不可能全在x轴上方，

△＝a²－36≥0，所以a≥6或a≤－6.

由x²－ax+9>0得x>或x<.

所以此函数的定义域为

(－∞，)∪(，+∞)．