
题目列表(包括答案和解析)
1.已知有穷数列: ,其中后一项比前一项大2.
,其中后一项比前一项大2.
⑴求此数列的通项公式;
⑵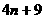 是否为此数列的项?
是否为此数列的项?
[解析]⑴设数列的第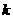 项为
项为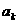 ,则
,则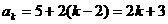
令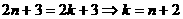 ,故该数列的通项公式
,故该数列的通项公式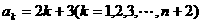
⑵令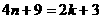 ,解得
,解得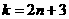 ,
,

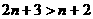 ,
, 
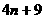 不是有穷数列的项.
不是有穷数列的项.
3.重难点:正确理解数列的概念,掌握数列通项公式的一般求法.
求数列的通项、判断单调性、求数列通项的最值等通常应用数列的有关概念和函数的性质.
问题1:已知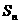 是数列
是数列 的前
的前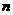 项和,
项和,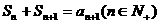 ,则此数列是( )
,则此数列是( )
A.递增数列 B.递减数列 C.常数数列 D.摆动数列
分析:将已知条件转化为数列项之间的关系,根据数列单调性作出判定.
解析:
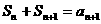 ,
,
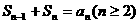
两式相减,得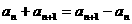 ,
,
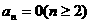
当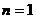 时,
时,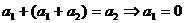 ,
,
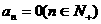 ,选C.
,选C.
问题2:数列 中,
中,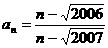 ,则该数列前100项中的最大项与最小项分别是( )
,则该数列前100项中的最大项与最小项分别是( )
A.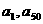 B.
B. 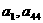 C.
C. 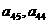 D.
D.
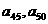
分析:由已知条件判定数列单调性,注意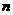 的取值范围.
的取值范围.
解析:
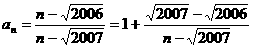 ,
,

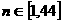 时,
时,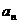 递减;
递减;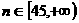 时,
时,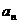 递减.结合图象,选C.
递减.结合图象,选C.
★ 热 点 考 点 题 型 探 析★
考点1 数列的通项公式
题型1 已知数列的前几项,求通项公式
[例1]求下列数列的一个通项公式:
⑴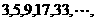
⑵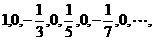
⑶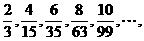
⑷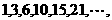
[解题思路]写出数列的通项公式,应注意观察数列中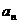 和
和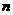 的联系与变化情况,应特别注意:自然数列、正奇数列、正偶数列,
的联系与变化情况,应特别注意:自然数列、正奇数列、正偶数列,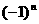 和相关数列,等差、等比数列,以及由它们组成的数列,从中找出规律性,并分别写出通项公式.
和相关数列,等差、等比数列,以及由它们组成的数列,从中找出规律性,并分别写出通项公式.
[解析]⑴联想数列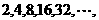 即数列
即数列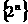 ,可得数列的通项公式
,可得数列的通项公式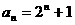 ;
;
⑵将原数列改写为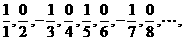 分母分别为
分母分别为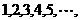 分子分别为
分子分别为
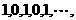 呈周期性变化,可以用
呈周期性变化,可以用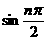 ,或
,或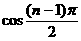 ,或
,或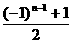 表示.
表示.
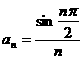 (或
(或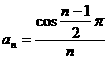 ,或
,或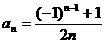 )
)
⑶分子为正偶数列,分母为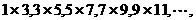 得
得 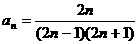
⑷观察数列可知: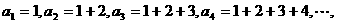
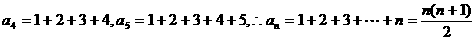
本题也可以利用关系式 求解.
求解.
[名师指引]⑴联想和转换是由已知认识未知的两种有效的思维方法.
⑵求数列的通项公式,应运用观察、分析、归纳、验证的方法.易错之处在于每个数列由前几项找规律不准确,以及观察、分析、归纳、验证这四个环节做的不够多,应注意对每一数列认真找出规律和验证.
题型2 已知数列的前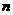 项和,求通项公式
项和,求通项公式
[例2]已知下列数列 的前
的前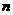 项和
项和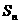 ,分别求它们的通项公式
,分别求它们的通项公式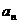 .
.
⑴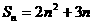 ; ⑵
; ⑵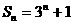 .
.
[解题思路]利用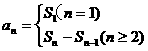 ,这是求数列通项的一个重要公式.
,这是求数列通项的一个重要公式.
[解析]⑴当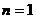 时,
时,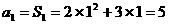 ,
,
当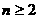 时,
时,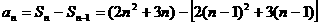
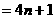 .
.
当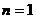 时,
时,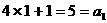 ,
,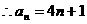 .
.
⑵当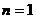 时,
时,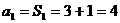 ,
,
当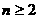 时,
时,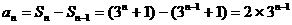 .
.
当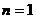 时,
时,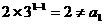 ,
,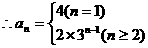 .
.
[名师指引]任何一个数列,它的前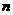 项和
项和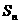 与通项
与通项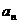 都存在关系:
都存在关系: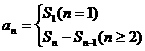
若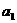 适合
适合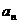 ,则把它们统一起来,否则就用分段函数表示.
,则把它们统一起来,否则就用分段函数表示.
题型3 已知数列的递推式,求通项公式
[例3]数列 中,
中,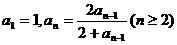 ,求
,求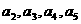 ,并归纳出
,并归纳出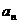 .
.
[解题思路]已知 的递推公式
的递推公式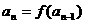 求前几项,可逐步计算.
求前几项,可逐步计算.
[解析]
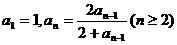 ,
,

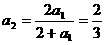 ,
,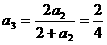 ,
,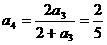 ,
,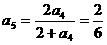 ,
,
由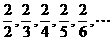 ,可以归纳出
,可以归纳出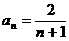 .
.
[名师指引]由递推公式求通项,可以考虑“归纳-猜想-证明”的方法,也可以构造新数列.
[新题导练]
2.难点:用函数的观点理解数列.
1.重点:理解数列的概念和几种简单表示方法;掌握数列的通项公式的求法.
6. 数列的分类:有穷数列,无穷数列;递增数列,递减数列,摆动数列,常数数列;有界数列,无界数列.
①递增数列:对于任何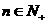 ,均有
,均有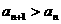 .
.
②递减数列:对于任何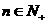 ,均有
,均有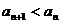 .
.
③摆动数列:例如: 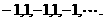
④常数数列:例如:6,6,6,6,…….
⑤有界数列:存在正数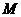 使
使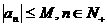 .
.
⑥无界数列:对于任何正数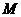 ,总有项
,总有项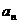 使得
使得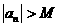 .
.
★ 重 难 点 突 破 ★
5. 数列的表示方法:解析法、图像法、列举法、递推法.
4.数列的前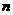 项和与通项的公式
项和与通项的公式
①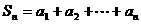 ; ②
; ②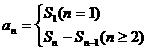 .
.
3.递推公式:如果已知数列 的第一项(或前几项),且任何一项
的第一项(或前几项),且任何一项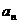 与它的前一项
与它的前一项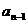 (或前几项)间的关系可以用一个式子来表示,即
(或前几项)间的关系可以用一个式子来表示,即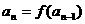 或
或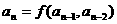 ,那么这个式子叫做数列
,那么这个式子叫做数列 的递推公式. 如数列
的递推公式. 如数列 中,
中,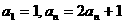 ,其中
,其中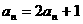 是数列
是数列 的递推公式.
的递推公式.
2.通项公式:如果数列 的第
的第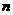 项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即
项与序号之间可以用一个式子表示,那么这个公式叫做这个数列的通项公式,即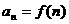 .
.
1.数列的定义:按照一定顺序排列的一列数称为数列,数列中的每个数称为该数列的项.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com