
题目列表(包括答案和解析)
6.数列 中,
中,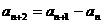 ,
,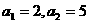 ,则
,则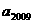 的值是( )
的值是( )
A. 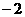 B.
B.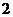 C.
C.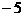 D.
D.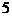
[解析]C.利用数列的周期性,除前4项后,周期为6,
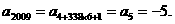
综合拔高训练
5.(2009恩城中学文)观察下式:1=12,2+3+4=32,3+4+5+6+7=52,4+5+6+7+8+9+10=72,…,则可得出一般结论 .
[解析]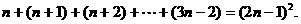
4.数列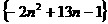 中数值最大的项是第 项.
中数值最大的项是第 项.
[解析]3
3.(2009恩城中学)已知定义在正整数集上的函数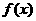 满足条件:
满足条件: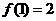 ,
,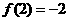 ,
,
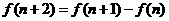 ,则
,则 的值为( )
的值为( )
A.-2 B. 2 C.4 D.-4
[解析]B.利用数列的周期性,周期为4,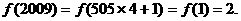
2.(2008年华师附中)数列 的前
的前 项和为
项和为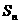 ,且
,且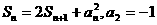 ,则数列
,则数列 的首项为( )
的首项为( )
A.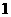 或
或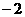 B.
B.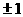 C.
C.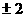 D.
D.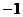 或
或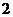
[解析]D.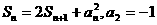 中令
中令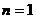 ,得
,得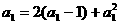 ,
,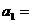
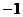 或
或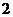
1.设数列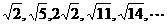 ,则
,则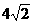 是这个数列的( )
是这个数列的( )
A.第9项 B.第10项 C.第11项 D.第12项
[解析]C.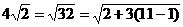 ,
, 选C.
选C.
5.数列 中,
中,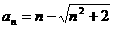 ,求数列
,求数列 的最大项和最小项.
的最大项和最小项.
[解析]
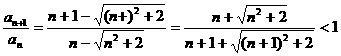 ,
,
又
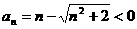 ,
,
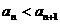 ,数列
,数列 是递增数列
是递增数列
 数列
数列 的最小项为
的最小项为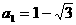 ,没有最大项.
,没有最大项.
★ 抢 分 频 道 ★
基础巩固训练
4.数列 中,
中,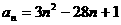 ,求
,求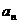 取最小值时
取最小值时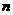 的值.
的值.
[解析]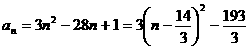 ,
,
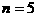 时,
时,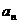 取最小值.
取最小值.
3.数列 中,
中,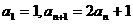 ,求
,求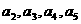 ,并归纳出
,并归纳出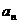 .
.
[解析]
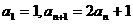

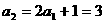 ,
,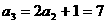 ,
,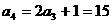 ,
,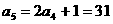
由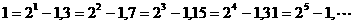 ,可以归纳出
,可以归纳出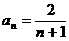
考点2 与数列的通项公式有关的综合问题
题型1 已知数列通项公式,求项数及最大(最小)项
[例4]数列 中,
中,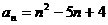 .
.
⑴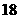 是数列中的第几项?
是数列中的第几项?
⑵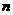 为何值时,
为何值时,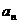 有最小值?并求最小值.
有最小值?并求最小值.
[解题思路]数列的通项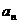 与
与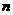 之间构成二次函数,可结合二次函数知识去探求.
之间构成二次函数,可结合二次函数知识去探求.
[解析]⑴由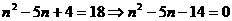 ,解得
,解得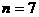 ,
,

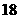 是数列中的第
是数列中的第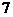 项.
项.
⑵
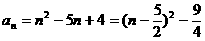 ,
,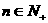

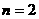 或
或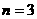 时,
时,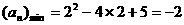 .
.
[名师指引]利用二次函数知识解决数列问题时,必须注意其定义域 为正整数.
为正整数.
题型2 已知数列通项公式,判断数列单调性及有界性
[例5]数列 中,
中,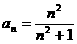 .
.
⑴求数列 的最小项;
的最小项;
⑵判断数列 是否有界,并说明理由.
是否有界,并说明理由.
[解题思路]⑴转化为判断数列的单调性,即证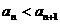 ,或
,或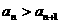 ;⑵从“数列的有界性”定义入手.
;⑵从“数列的有界性”定义入手.
[解析]⑴
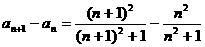
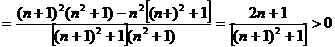

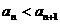 ,
, 数列
数列 是递增数列,数列
是递增数列,数列 的最小项为
的最小项为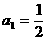 .
.
⑵
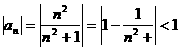 ,
, 数列
数列 有界.
有界.
[名师指引]数列是特殊的函数,判断函数的单调性、有界性的方法同样适用于数列.
[新题导练]
2.数列 中,
中,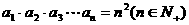 ,求
,求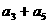 的值.
的值.
[解析]由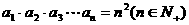 ,得
,得
当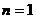 时,
时,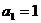 ;当
;当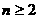 时,
时,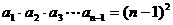
两式相除,得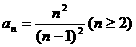 .
.
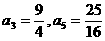 ,
,
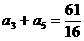 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com