年级 　　　班　　　 姓名　　 　得分　　

14.　 设此四人为甲、乙、丙、丁并用画在平面上的四个点分别表示他们，称为它们的代表点,当某人(例如甲)赠了1件礼品给另一个(例如乙)时,就由甲向乙的代表点画一条有指向的线,无非有以下两个可能:

(1)甲、乙、丙、丁每人各收到了2件礼品.

(2)上面的情形不发生.这时只有以下一个可能,即有一个人接受了3件礼品

(即多于2件礼品；因为一人之外总共还有三个人，所以至多收到3件礼品).(或许会有人说,还有两个可能:有人只收到1件礼品及有人什么礼品也没收到.其实,这都可归以“有一人接受了3件礼品”这个情形.因为,当有一人(例如甲)只接受了1件礼品的情形发生时,四人共带来的8件礼品中还剩下7件在甲以外的三个人中分配,如果他们每人至多只收到2件礼品,则收受礼品数将不超过6件,这不可能,所以至少有一人收到2件以上(即3件)礼品,同样,当甲未收到礼品时,8件礼品分给乙、丙、丁三人，也必定有人收到3件礼品).

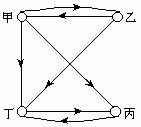
当(1)发生时,例如甲收到乙、丙的礼品,由于甲发出的礼品中至少有1件给了乙或丙,为确切计,设乙收到了甲的礼品,于是我们先有了一对人:(甲、乙),他们互赠了礼品，如果丙也收到甲的礼品,那么又有了第二对互赠了礼品的人(甲、丙)；如果收到甲礼品的另一人是丁(如右图)丁的2件礼品必定分赠了乙及丙(甲已收足了本情形中限定的2件礼品)丙或乙的另一件礼品给了丁,则问题也解决(这时另一对互赠了礼品的人便是(乙、丁)或(丙、丁)但丙的另一件礼品只能给丁,因为这时乙已收足了2件礼品,所以，当本情形发生时,至少能找到两对互赠过1件礼品的人.

当(2)发生时,不失一般性,设甲收到了来自乙、丙、丁的各1件礼品，但甲又应向他们之中的某两人(例如乙、丙)各赠送1件礼品,于是(甲、乙),(甲、丙)便是要找的两对人.总上可知,证明完毕.

13.表解如下:

老吴是业余画家,老周是业余音乐家,老杨是业余作家. 　 工	会	农		作	画	音
´	´		吴	´	√	´
´			周	´	´	√
			杨	√	´	´

工程师是老杨,会计师是老周农艺师是老吴. 　 工	会	农		作	画	音
´	´	√	吴	´	√	´
´	√	´	周	´	´	√
√	´	´	杨	√	´	´

12.用表格解如下:

北	上	浙	吉		游	田	乒	足
张明是北京选手 李勇是吉林选手 　 √	´	´	´	张	´	´
´			´	胡			´	´
´	´	´	√	李			´
´			´	郑	´

北	上	浙	吉		游	田	乒	足
由(3)北京运动员不是乒乓球运动员, 故张是足球运动员,郑是乒乓球运动员 　 √	´	´	´	张	´	´	´	√
´			´	胡			´	´
´	´	´	√	李			´	´
´			´	郑	´	´	√	´

由(4)吉林运动员不是游泳运动员, 故李是田径运动员,而胡是游泳运动员 　 北	上	浙	吉		游	田	乒	足
√	´	´	´	张	´	´	´	√
´			´	胡	√	´	´	´
´	´	´	√	李	´	√	´	´
´			´	郑	´	´	√	´

北	上	浙	吉		游	田	乒	足
√	´	´	´	张	´	´	´	√
由(5)知胡是上海 运动员而郑是浙江运动员. 　 ´	√	´	´	胡	√	´	´	´
´	´	´	√	李	´	√	´	´
´	´	√	´	郑	´	´	√	´

11.刘毅和小红,马宏明和小英,张健和小萍分别是兄妹.　

		萍	英	红
	刘	´
	马			´
	张		´	´
	萍	英	红
刘	´	´	√
马	´	√	´
张	√	´	´

10.　 蓝、黄、红.

解法一

题中表明,每个孩子的父母是同血型的.具有B型血的孩子,其父母同血型时,由表中可见,只能是B型或AB型,但题中没有同具B型血的父母,所以戴红帽子的父母的孩子穿蓝上衣.具有A型血的孩子的同血型的父母,只可能同为A型血或同为AB型血.今已知有一对父母为AB型血者,所以穿黄上衣的孩子的父母戴黄帽子.由表中可见,其孩子为O型血时,父母血型只能同为A型或B型或O型.今已知不具有同为B型血的父母,而同为A型血的父母的孩子已知具有A型血.把代表孩子的点与他的可能双亲的代表点之间连一直线段,便可得下面的图；由于孩子与其父母之间是唯一搭配的,所以,保存下来的只有连着红、蓝；黄，黄及蓝，红的三条边.

所以,穿红上衣(O型血)孩子的父母戴蓝帽子.

孩子衣服颜色　　　　　　　 父母帽子颜色

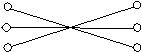(O型血)红　　 　　　　　　红(AB型血)

(A型血)黄　　　　　　　　 黄(A型血)

(B型血)蓝　　　　　　　　 蓝(O型血)

所以,穿红上衣的孩子的父母戴蓝帽子；穿黄上衣的孩子的父母戴黄帽子；穿蓝上衣的孩子的父母戴红帽子.

9.　 5

根据题意,有11名队员比赛场数各不相同,并且每人最多比赛10场,所以除

甲外的11名队员比赛的场数分别为0~10.

已赛10场的队员与除已赛0场外的所有队员都赛过,所以已赛10场的队员

与已赛0场的队员同班；

已赛9场的队员与除已赛0、1场外的所有队员都赛过,所以已赛9场的队员与已赛1场的队员同班；

同理,已赛8、7、6场的队员分别与已赛2、3、4场的队员同班；所以甲与已赛5场的队员同班,即乙赛过5场.

注 本题可以求出甲也赛了5场,分别与已赛10、9、8、7、6场的队员各赛1场.

8.　 51天.

因为[8,6,4]=24,所以四人去图书馆的情况每24天循环一次(见下表):

每24天有4天只有1人去图书馆.3月1日至12月31日有306天,　　　　

306¸24=12…18，所以所求天数为4´12+3=51(天).

3.因为每人猜对的数字不相邻,所以张、李猜对的另一个数字都在前两位,王猜对的两个数字是7和5,进而推知张猜对9,李猜对1.电话号码是19735.

7.　 19735.

因为每个数字都有人猜对,所以每人至少猜对两个数字.下页右上图中,同一位数中只有方框中的两个数相同,如果每人猜对的数字多于两位,相同的数字至少有3´3-5=4(组),所以每人恰好猜对两个数字.　　　　 王: 9 3 7 1 5

三人共猜对2´3=6(个)数字,因为电话号码只有　　　　　 张: 7 9 5 3 8

5位,所以相同的一组是正确的,即左起第四位是　　　　 李: 1 5 2 3 9