线段垂直平分线的性质定理　 线段垂直平分线上的点到这条线段两个端点的距离相等。

下面我们就来证明这个定理。

如图，已知线段AB，直线EF⊥AB，垂足为O，AO=BO，点P是EF上异于点 O的任意一点。

求证：PA=PB。

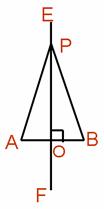
证明：∵EF⊥AB(已知)，

∴∠POA=∠POB=90°(垂直的定义)。

在△PAO和△PBO中，

AO=BO(已知)，

∠POA=∠POB(已证)，

PO=PO(公共边)，

∴△PAO≌△PBO(SAS)。

∴PA=PB。

1.已知一次函数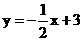

(1)x取何值时，y的值等于2？

(2)x取何值时，y的值都大于2？x取何值时，y的值都小于2？

借助一次函数的图像解方程组

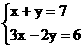
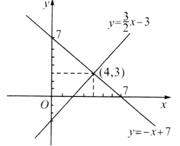
在同一坐标系中画出y=－x+7与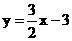的图像，由交点坐标知

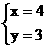
例　 已知函数y₁=－2x+3和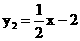

(1)x取何值时，y₁=y₂?

(2)x取哪些值时，y₁>y₂?

(3)x取哪些值时y₁<y₂?

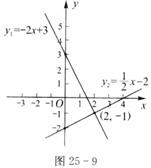
解：(1)要使y₁=y₂，就是要使

－2x+3=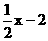

解这个方程，得x=2

即当x=2时，y₁=y₂。

(2)要使y₁>y₂，就是要使－2x+3>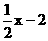

解这个不等式，得x<2。

即当x<2时，y₁>y₂。

(3)要使y₁<y₂，就是要使－2x+3<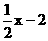

解这个不等式，得x>2。

即当x>2时，y₁<y₂。

由图25-9中的图像也可以看出：这两个函数图像的交点是(2，－1)，也就是当x＝2时，y₁和y₂的值相等，都等于－1；当x<2时，y_l=－2x+3的图像在y₂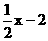＝的图像的上方，这说明此时y₁>y₂；当x>2时，y_l=－2x+3的图像在y₂=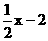的图像的下方，这说明此时y₁<y₂。

已知一次函数y=2x－1。

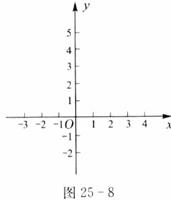
(1)在图25-8的直角坐标系中，画出它的图像。

(2)对这个一次函数，x取何值时，它所对应的y的值等于5?x取哪些值时，它们所对应的y的值都大于5?x取哪些值时，它们所对应的y的值都小于5?

(3)由图像上点的坐标，对(2)中各问题的结论作出解释。

注：目的在于使学生通过动手操作，从形与数两个角度体会一次函数与方程、不等式的内在联系。

容易看到，对一次函数y=2x－1，求“x取何值时，它所对应的y的值等于5”，就是求一元一次方程

2x－1=5

的解；求“x取哪些值时，它们所对应的y的值都大于(或小于)5”，就是求一元一次不等式2x－1>5(或2x－1<5)的解集

由此看到，一次函数与一元一次方程、一元一次不等式有着密切的联系。

我们曾经学习过一元一次方程、一元一次不等式以及二元一次方程组，现在又学习了一次函数。你是否想过，它们既然都是“一次”的，其中会不会有什么内在的联系呢？

25.1 一次函数

第1题. 某工厂加工一批产品，为了提前完成任务，规定每个工人完成150个以内，按每个产品3元付报酬，超过150个，超过部分每个产品付酬增加0.2元；超过250个，超过部分出按上述规定外，每个产品付酬增加0.3元，求一个工人：

①完成150个以内产品得到的报酬y(元)与产品数x(个之间的函数关系式；

②完成150个以上，但不超过250个产品得到的报酬y(元)与产品数量x(个)的函数关系式；

③完成250个以上产品得到的报酬y(元)与产品数量x(个)的函数关系式．

答案：①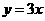　(0＜x≤150)；

②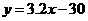　　 (150＜x≤250)；

③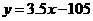　　 (x＞250)

第2题. 商品的销售量也受销售价格的影响，比如，某衬衣定价为100元时，每月可卖出2000件，价格每上涨10元，销售量便减少50件.那么，每月售出衬衣的总件数y(件)与衬衣价格x(元)销售之间的函数关系式为_________．

答案：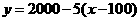

第3题. 写出下列函数关系式，并指出自变量的取值范围：油箱中有油60升，每小时耗油2升，求耗油量M与时间t(小时)的关系．

答案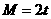：(0≤t≤30)

第4题. 写出下列函数关系式，并指出自变量的取值范围：

轮子每分钟转60圈，求轮子旋转的转数N与时间t(分)的关系

答案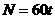：(t≥0)

第5题. 下列关于函数的说法中，正确的是(　)

A． 一次函数是正比例函数

B． 正比例函数是一次函数

C． 正比例函数不是一次函数

D． 不是正比例函数的就不是一次函数

答案：B

第6题. 等腰三角形的周长为20cm，腰长为y (cm)，底边长为x(cm)，则y与x的函数关系式为______．

答案：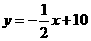

第7题. 若函数y=(m-3)x^m-1+x+3是一次函数，且x≠0，则m的值为______．

答案：2或1

第8题. 一次函数y=kx+b中，k、b都是　　　 ，且k 　　　，自变量x的取值范围是　　　 ，当k　　　 ，b　　　 时，它是正比例函数．

答案：常数，≠0,全体实数，≠0，=0

第9题. 观察图形

上图中每个小正方形都是由四根火柴秆组成的，那么火柴秆的数量y(根)与小正方形的个数n的关系为　　　 ．

答案：. y=3n+1(n为1、2、3、4、…….)

第10题. △ABC中，一边长为x cm，这边上的高为4cm，面积为y cm²，那么y与x之间的函数关系式为　　　 ．

答案：y=2x

第11题. 出租车收费按路程计算，2km内(包括2km)收费3元，超过2km，每增加1km加收1元，则路程x≥2km时，车费y(元)与x之间的函数关系为____．

答案：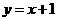

第12题. 拖拉机开始工作时，油箱中有油36L，如果每小时耗油4L，那么油箱中剩余油量y(L)，与工作时间x(h)之间的函数关系式是____，自变量x的取值范围是____．

答案：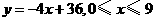

第13题. 《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元的部分不必交税，超过800元的部分为全月应纳税所得额，此项税款按下表分段累计进行计算：

全月应纳税所得额　　 税率　　

不超过500元的部分　 5%　

超过500元至2000元的部分　 10%

超过2000元至5000元的部分　 15%

……　　 ……　　

某合资企业一工人工资在1400元-2000元之间变化，求他应交税金y(元)与其工资x(元)之间的函数关系．

答案：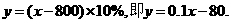

第14题. 出租车收费按路程计算，2km内(包括2km)收费3元，超过2km，每增加1 km加收1元，则路程x≥2 km时，车费y(元)与路程x(km)之间的函数关系为______．

答案：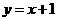

第15题. 将长为30cm，宽为10cm的长方形白纸，按图所示的方法粘合起来，粘合部分的宽为3cm，则5张白纸粘合后的长度是多少？设x张白纸粘合后的总长度为y(cm)，y与x之间的函数关系式是什么？

[来源:Z&X&X&K]

答案：138cm，y=30x-3(x-1)=27x+3.

第16题. 已知y+a与x-b成正比例(其中a、b都是常数)，试说明：y是x的一次函数

答案：设y+a=k(x-b)(x≠0)

y=kx-(a+bk)

第17题. 已知y+a与x-b成正比例(其中a、b都是常数)

(1)试说明y是x的一次函数；

(2)如果x=-1时，y=-15；x=7时，y=1，求这个一次函数的解析式．

答案：(1)因为y+a与x-b成正比例，所以y+a=k(x-b)(k≠0),即y=kx-(bk+a)因为k不等于0，a、b为常数，所以y是x的一次函数;

(2)代入解得k=2,bk+a=13, 所以y=2x-13.

第18题. 下列关于函数的说法中，正确的是(　)

A． 一次函数是正比例函数

B． 正比例函数是一次函数

C． 正比例函数不是一次函数

D． 不是正比例函数的就不是一次函数

答案：B

第19题. 汽车由天津开往相距120km的北京，若它的平均速度为60km/h，则汽车距北京的路程S(km)与行驶时间t(h)之间的函数关系式是______．

答案：S=120-60t

第20题. 两港相距640千米，轮船以15千米/时的速度航行，t小时后剩下的距离y与t的函数关系式为________．

答案：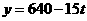

第21题. 某种国库卷的年利率为9.18%， 则存满三年的本息和y与本金x之间的函数关系式为　　　　 ．

答案：y=x+3×9.18%x(x＞0)

第22题. 一个长为120m，宽为100m的矩形场地要扩建成一个正方形场地，设长增加x米,宽增加y米，则y与x的函数关系式是　　 ，自变量的取值范围是　　 ，且y是x的　　 函数．

答案：y=x+20,x≥0,一次

第23题. 点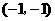　　(填：“在”或“不在”)直线

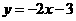上

答案：在

2．边长相等的正三角形和正六边形彩纸若干张。

25.1 一次函数教学设计

教学目标

知识与技能：知道一次函数与正比例函数的意义及区别联系。能写出实际问题中的一次函数的解析式。

过程与方法：经历从具体问题情景中建立一次函数的数学模型的过程，使用并体会到数学的抽象性和广泛的应用性。

情感、态度、价值观：体会现实生活中存在着大量的函数关系，学习一次函数的有关知识是生活和工作的需要。使学生真正懂得“数学源于生活”，激发学生爱国主义思想和求知欲。

教学重点：一次函数与正比例函数概念的理解。

教学难点：根据具体条件求出一次函数与正比例函数的解析式。

教学方法：结构教学法、以学生“再创造”为主的教学方法。

教材分析：一次函数是函数学习的基础。掌握一次函数的意义、特点、应用对以后学习函数有着非常重要的意义。

本节课首先实际问题入手，引入一次函数的定义，函数关系式，在定义它的特例--正比例函数及其意义，让学生逐步掌握一次函数的线性特点，并会用这些特点使一次函数的不同表达方法相互转化。根据实际问题、具体要求选用适当的表示方法来解决相关问题。提高学生解决实际问题的能力，使学生数学与现实世界的内在联系，鼓励他们有条理地表达和思考，培养其学习的兴趣。

课前准备：

教师准备：1、多媒体课件。