
题目列表(包括答案和解析)
3.教师引导学生自主研究得出结论,在自主学习中,教师要较好地扮演促进者、协作者、组织者的角色。数学教学的过程是师生共活动,共同成长与发展的过程,学生也是课程资源的 开发者,如本课例中学生一时
开发者,如本课例中学生一时 得不出一次函数性质的内容,教师引导的过程就是充满机智的过程。通过充分的过程探究,学生终于得出y=kx及y =kx+b的性质。
得不出一次函数性质的内容,教师引导的过程就是充满机智的过程。通过充分的过程探究,学生终于得出y=kx及y =kx+b的性质。
2.允许学生质朴而真实的说法
如学生说的“走 向”,“向上爬”,“下降”等,逐步过渡到用数学语言来描绘事物。
向”,“向上爬”,“下降”等,逐步过渡到用数学语言来描绘事物。
1.尊重学生实际,让学生在自主学习中提高。
首先设计适合学生探究的素材。学生动手写出一次函数的表达式,又分别观察了这些一次函数分了几 种类型,回顾了一次函数图像的画法使他们动手画这些图像时非常顺利的进行,在画出图像后,教师
种类型,回顾了一次函数图像的画法使他们动手画这些图像时非常顺利的进行,在画出图像后,教师 因势利导引导学生观察一次函数“图像的性质”,把一次
因势利导引导学生观察一次函数“图像的性质”,把一次 函数的性质研究直观地转化为对图像“增减性”的研究,再从“图像”的性质轻松理解一次函数的性质。
函数的性质研究直观地转化为对图像“增减性”的研究,再从“图像”的性质轻松理解一次函数的性质。
25.2 一次函数的图像和性质
第二课时教学课例
研究 背景:
背景:
本节课是让学生通过具体操作与探究,在探究活动中去经历、体验、内化知识,才能收到好的教学效果。通过充分的过程探究,学生得出图像性质,再借助图像直观的性质进而得到一次函数的性质。放手探究,让学生的潜力与智慧充分表现出来 ,使他们的真实
,使他们的真实 思维
思维 和真实自我有机会得到释放和张扬。
和真实自我有机会得到释放和张扬。
教学设计:
第一步 知识回顾
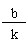 一次函数的一般表达式是y=kx+b(k,b为常数,k≠0)让学
一次函数的一般表达式是y=kx+b(k,b为常数,k≠0)让学 生写出一些常数较简单的一次函数表达式。
生写出一些常数较简单的一次函数表达式。
画一次函数图像,只需确定两个点(0,b),(- , 0),过这两点作直线。
第二步 动手操作
让学生到前面写出10个一次函数表达式。
让学生说出这些一次函数大致有几种类型。
师写
 出8个常数简单的一次函数表达式,让学生画出这八个函数的图像(分成8个 小组,6人一组,每组一个),师巡视、指导。
出8个常数简单的一次函数表达式,让学生画出这八个函数的图像(分成8个 小组,6人一组,每组一个),师巡视、指导。
第三步 观察与思考﹣
它们的图像在直角坐标系中位置一样吗?
引导学生从图像变化 趋势上观察并分类探索表达式y=kx+b 与图像间的关系。
趋势上观察并分类探索表达式y=kx+b 与图像间的关系。
第四步 一起探究 得出结论
指 明探究方向,它们的位置不一样是由什么要素决定的?(分类探究)
明探究方向,它们的位置不一样是由什么要素决定的?(分类探究)
由图像性质得出一次函数的性质(直观性语言描述)
从自变量x与函数y之间的变化角度来说明(师引导,生说结论)
教学片段
……
师 :一次函数的表达式是y=kx+b(k,b为常数,k≠0),请同学们在黑板上写出一些常数较简单的一次函
:一次函数的表达式是y=kx+b(k,b为常数,k≠0),请同学们在黑板上写出一些常数较简单的一次函 数表达式行吗?
数表达式行吗?
 (学生表现踊跃,写出了10多个)
(学生表现踊跃,写出了10多个)
师:你们认为黑板上这些一次函 数大致有几种类型?
数大致有几种类型?
生:(讨论一会儿后)四类,即k﹥0,b>0;k>0,b<0;k<0,b>0;k<0,b<0。
(老师在学生板书的函数中不同类型各选了两个,并把常数较复杂的更换成简单的常数,即y=3x+2,y=-2x+3,y=x+1,y=-x+2,y=-2x-2,y=x-2,y=-x-3,y=2x-1)
师:我们来画出这八个函数的图像。
(把任务分配给了8个小组,每组1个,6人一组,在坐标系已画好的黑板上动手操作)(学生在自己提供的素材上进行再“加工”,兴趣很大,教师到每组巡视、指导。在确认画图全部正确的情况下 ,老师提出了要求)
,老师提出了要求)
师:请同学们组间比较一下,你们的图像在直角坐标系中位置一样吗?
生:(互相探视后)“不一样”,“有些一样”……
师:有什么不一样?(开始聚焦矛盾)
生:(七嘴八舌)“走 向不一样
向不一样 ”,“经过的象限不一样”,“我们的图像在原点上方”
”,“经过的象限不一样”,“我们的图像在原点上方” ,“我们的图像在原点下方”……
,“我们的图像在原点下方”……
师:看来有些不一样,那么它们位置的不一样是由什么要素决定的?(教师指明了探究方向,但未指明具体的探究之路是明智的)
生1:是由k、b的取值确定的。
师:很好!我们围绕生1的回答,能得到图像或函数的哪些结论?(顺水推舟,放手让学生一搏)
(热烈讨论后)
生 2(板书):当k>0时,图像从“左下”到“右上”;当k<0 时,图像从“左上”到“右下”。3(板书):当b >0时,图像在原点上
2(板书):当k>0时,图像从“左下”到“右上”;当k<0 时,图像从“左上”到“右下”。3(板书):当b >0时,图像在原点上 方;当b <0时,图像在原点下方。
方;当b <0时,图像在原点下方。
生4(板书):当k>0,b>0 时,图像经过一、二、三象限。
(生5、生6跑到黑板前补充:当事人k>0,b<0时,图像经过一、三、四象限;当k<0,b>0时,图像经过一、二、四象限;当k<0,b<0时,图像经过二、三、四象限)
(这个探究过程约用了10多分钟,学生体会非常充 分,从学生的神情看,绝大多数学生已接受几位同学的板书,但老师未对结论进行优化。这时倒使老师为难了,怎么没有一个学生说出一次函数的性质呢?短暂局促与紧张后,老师确定了思路)
分,从学生的神情看,绝大多数学生已接受几位同学的板书,但老师未对结论进行优化。这时倒使老师为难了,怎么没有一个学生说出一次函数的性质呢?短暂局促与紧张后,老师确定了思路)
师:刚才你们研究了图像的性质,能否由图像性质得出相应函数的性质呢?
(学生茫然)
师:请看生2的板书,能揣摩图像“走向”的意思吗?
生(七嘴八舌):当k>0时,图像向上“爬”;当k<0时,图像向下“走 ”……(未出现老师所预期的结论)
师:好,大家能很贴切地从图像的直观形象来理解图像性质,能不能从自变量x与函数y之间的变化的角度来说明 “向上爬”、“向下走”的含义呢?
“向上爬”、“向下走”的含义呢?
生众:当k>0时,x与y 同向变化,k<0时,x与y异向变化……
师:也就是说,k>0,x增大,y……
生众:增大。
师:k<0时,x……y……
生众:x增大,y减小;x减小,y增大。
(在这里,老师努力避免了知识的“告诉”方式工,而是间接引导)
师:好了,我 们就用x与y 之间的变化规律来表达一次函数的性质好吗?请同学们在书上补充图像的性质,并熟悉一
们就用x与y 之间的变化规律来表达一次函数的性质好吗?请同学们在书上补充图像的性质,并熟悉一 下一次函数的性质。
下一次函数的性质。
……
教学反思
25.2 一次函数的图像和性质
第1题. 对于任何实数x,点M(x,x-3)一定不在第几象限?
答案:点M(x,x-3)在直线y=x-3上,而直线y=x-3不过第二象限,所以,对于任何实数x,点M(x,x-3)一定不在第二象限.
第2题. 一次函数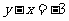 ,如果
,如果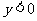 ,则x的取值范围是( )
,则x的取值范围是( )
A.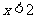 B.
B.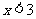 C.
C. D.
D.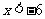
答案:B.
第3题.
 已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论:①k>0,b>0;②k>0,b<0;③k<0,b>0;④k<0,b<0.其中正确的结论的个数是( )
已知直线y=kx+b(k≠0)与x轴的交点在x轴的正半轴,下列结论:①k>0,b>0;②k>0,b<0;③k<0,b>0;④k<0,b<0.其中正确的结论的个数是( )
A.1 B.2 C.3 D.4
答案:B
第4题.
如图所示, 函数y=mx+m的图像中可能是( )
函数y=mx+m的图像中可能是( )
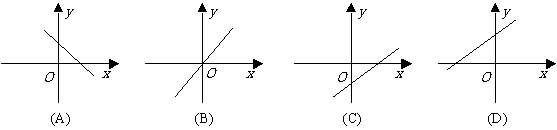 答案:D
答案:D
第5题. 当自变量x增大时,下列函数值反而减小的是( )
A. y=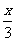 B.y=2x
B.y=2x
C.y=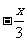 D.y=-2+5x
D.y=-2+5x
答案:C
第6题.  正比例函数的图像如图,则这个函数的解析式为( )
正比例函数的图像如图,则这个函数的解析式为( )
A.y=x B.y=-2x
C.y=-x D.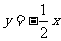
答案: C
C
第7题. 直线y=(2-5k)x+3k-2不过第一象限,则k需满足  ,写出一个满足上述条件的一个函数的解析式 .
,写出一个满足上述条件的一个函数的解析式 .
答案: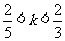 ,
,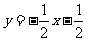
第8题. 直线y=4x-2与x轴的交点是 ,与y轴的交点是 .
答案: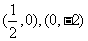
第9题. 直线y=(2-5k)x+3k-2若经过原点 ,则k= ;若直线与x轴交于点(-1,0),则k= ,
,则k= ;若直线与x轴交于点(-1,0),则k= ,
答案: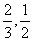
第10题. 一次函数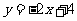 的图像经过的象限是____,它与x轴的交点坐标是____,与y轴的交点坐标是____,
的图像经过的象限是____,它与x轴的交点坐标是____,与y轴的交点坐标是____, y随x的增大而____.
y随x的增大而____.
答案:一、二、四象限,(2,0),(0,4),减小
第11题. (1)已知关于x的一次函数y=(2k-3)x+k-1的图像与y轴交点在x轴的上方,且y随x的增大而减小,求k的取值范围;
(2)已知函数y=(4m-3)x是正比例函数,且y随x的增大而增大,求m的取值范 围.
围.
答案:(1)依题意,有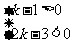 ,解得
,解得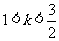 ;
;
(2)依题意,得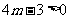 ,即
,即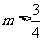 时,y随x的增大而增大.
时,y随x的增大而增大.
第12题.
已知一次函数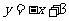 ,当0≤x≤3时,函数y的最大值是( ).
,当0≤x≤3时,函数y的最大值是( ).
A.0 B.3 C.-3 D.无法确定
答案:B点拔:画图得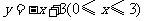 的图象是一条线段,又
的图象是一条线段,又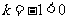 ,故y随x的增大而减小,∴当x=0时,y的最大值等于3
,故y随x的增大而减小,∴当x=0时,y的最大值等于3
第13题. 下列图像中,不可能是关于x的一次函数y=mx-(m-3)的图像的是( )
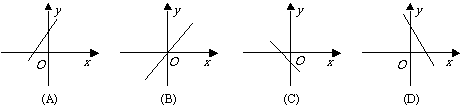
答案:C
第14题.
在同一坐标内,函数关系式为y=k x+b(k、b为常数且k≠0)的直线有无数条,在这些直线中,不论怎样抽取,至少要抽几条直线,才能保证其中的两条直线经过完全相同的象限( )
x+b(k、b为常数且k≠0)的直线有无数条,在这些直线中,不论怎样抽取,至少要抽几条直线,才能保证其中的两条直线经过完全相同的象限( )
A.4 B.5 C. 6 D.7
6 D.7
答案:D
第15题. 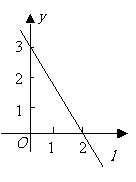 如图,直线l是一次函数y=kx+b的图像,看图填空:
如图,直线l是一次函数y=kx+b的图像,看图填空:
(1) b=______,k=______;
(2) x=-20时,y=_______;
(3) 当y=-20时,x=_______.
答案: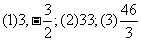
第16题. 若一次函数y=kx+b交于y轴的负半轴,且y的值随x的增大而减小,则k_____0,b______0.(填">"、"="、或"<")
答案:<,<
第17题. 下列各点(1,2),(-2,1),(1,-2),(-1,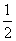 ),在y=-2x图像上有:____________.
),在y=-2x图像上有:____________.
答案:(1,-2)
第18题. 若一次函数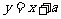
 与一次函数
与一次函数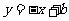
 的图像的交点坐标为(m,8).则a+b=______.
的图像的交点坐标为(m,8).则a+b=______.
答案:16
第19题. 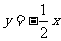 的图像上有两点
的图像上有两点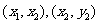 ,知
,知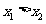 ,你能说出
,你能说出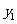 与
与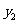 有什么关系吗?
有什么关系吗?
答案:
第20题. 如图,函数y=kx-2中,y随x的增大而减小,则它的图像是( )
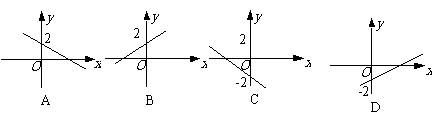 答案:C
答案:C
第21题.
若一次函数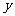 =k
=k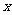 +b的图象经过一、三、四象限,则k,b应满足( )
+b的图象经过一、三、四象限,则k,b应满足( )
A.k>0,b>0 B.k>0,b<0
C.k<0,b>0 D.k<0,b<0
答案:B
第22题. 一次函数y=-3x-4与x轴交于( ),与y轴交于( ),y随x的增大而___________.
答案: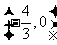 ,
,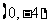 ,减少
,减少
第23题. 如果正比例函数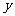 =3
=3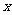 和一次函数
和一次函数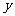 =2
=2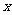 +
+ k的图象的交点在第三象限,那么k的取值范围是
.
k的图象的交点在第三象限,那么k的取值范围是
.
答案:k< 0
0
第24题. 已知点A(-4,a)、B(-2,b)都在直线y=0.5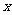 +k(k为常数)上,则a与b的大小关系是a b.(填"<""=" 或">")
+k(k为常数)上,则a与b的大小关系是a b.(填"<""=" 或">")
答案:<
第25题. 已知正比函数y=kx(k≠0)的函数值y随x的增大而减小,则一次函数y=x+k的图象大致是下图中的( )
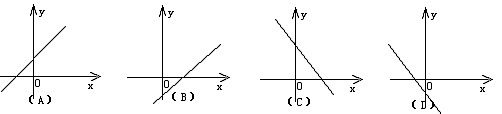
答案:B
第26题. 某校八年级同学到距学校6千米的郊外春游,一
部分同学步行,另一部分同学骑自行车,沿相同路线前往.
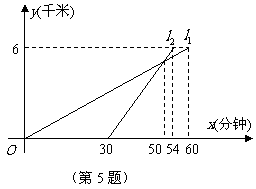 如图,
如图,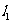 、
、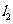 分别表示步行和骑车的同学前往目的地所走
分别表示步行和骑车的同学前往目的地所走
的路程 (千米)与所用时间
(千米)与所用时间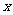 (分钟)之间的函数图象,
(分钟)之间的函数图象,
则以下判断错误的是 ( )
A.骑车的同学比步行的同学晚出发30分钟
B.步行的速度是6千米/时
C.骑车的同学从出发到追上步行的同学用了20分钟
D.骑车的同学和步行的同学同时到达目的地
答案:D
第27题. 一次函数y=kx+3的 图象与坐标轴的两个交点之间的距离为5,则k的值为 .
图象与坐标轴的两个交点之间的距离为5,则k的值为 .
答案: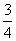 或
或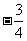
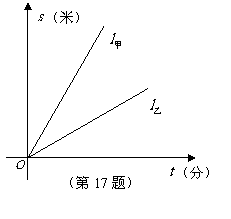
第28题. 如图,射线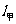 、
、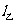 分别表示甲、乙两名运动员在自行车比赛中所行路程
分别表示甲、乙两名运动员在自行车比赛中所行路程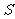 (米)与时间
(米)与时间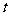 (分)的函数图象.则他们行进的速度关系是
(分)的函数图象.则他们行进的速度关系是
A.甲、乙同速 B.甲比乙快
C.乙比甲快 D.无法确定
 答案:B
答案:B
第29题. 已知函数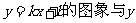 轴交点的纵坐标为
轴交点的纵坐标为 ,且当
,且当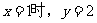 ,则此函数的解析式为 .
,则此函数的解析式为 .
答案: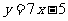
第30题. 甲、乙两同学从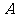 地出发,骑自行车在同一条路上行驶到
地出发,骑自行车在同一条路上行驶到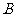 地,他们离出发地的距离
地,他们离出发地的距离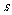 (千米)和行驶时间
(千米)和行驶时间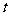 (小时)之间的函数关系的图象如图所示.根据图中提供的信息,有下列说法:
(小时)之间的函数关系的图象如图所示.根据图中提供的信息,有下列说法:
(1)他们都行驶了18千米;
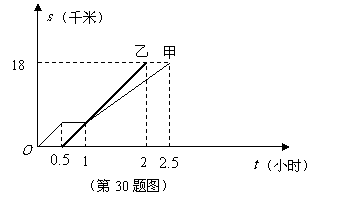 (2)甲在途中停留了0.5小时;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地.
其中符合图象描述的说法有
A.2个 B.3个 C.4个 D.5个
答案:C
第31题. 我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车 最远能到达 公里处.
最远能到达 公里处.
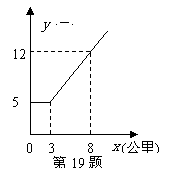

答案:13
3.教师引导学生 自主研究得出结论,在自主学习中,教师要较好地扮演促进者、协作者、组织者的角色。数学教学的过程是师生共活动,共同成长与发展
自主研究得出结论,在自主学习中,教师要较好地扮演促进者、协作者、组织者的角色。数学教学的过程是师生共活动,共同成长与发展 的过程,学生也是课程资源的开发者,如本课例中学生一时得不出一次函数性质的内容,教师引导的过
的过程,学生也是课程资源的开发者,如本课例中学生一时得不出一次函数性质的内容,教师引导的过 程就是充满机智的过程。通过充分的过程探究,学生终于得出y=kx及y =kx+b的性质。
程就是充满机智的过程。通过充分的过程探究,学生终于得出y=kx及y =kx+b的性质。
1.尊重学生实际,让学生在自主学习中提高。
首先设计适合学生探究的素材。学生动手写出一次函数的表达式,又分别观察了这 些一次函数分了几种类型,回顾了一次函数图像的画法使他们动手画这些图像时非常顺利的进行,在画出图像后,教师因势利导引导学生观察一次函数“图像的性质”,把一次函数的性质研究直观地转化为对图像“增减性”的研究,再从“图像”的性质轻松理解一次函数的性质。
些一次函数分了几种类型,回顾了一次函数图像的画法使他们动手画这些图像时非常顺利的进行,在画出图像后,教师因势利导引导学生观察一次函数“图像的性质”,把一次函数的性质研究直观地转化为对图像“增减性”的研究,再从“图像”的性质轻松理解一次函数的性质。
2 .允许学生质朴而真实的说法
.允许学生质朴而真实的说法
如学生说的“走向”,“向上爬”,“下降”等,逐步过渡到用数 学语言来描绘事物。
学语言来描绘事物。
25.2 一次函数的图像和性质
第二课时教学课例
研究背景:
本节课是让学生通过具体操作与探究,在探究活动中去经历、体验、内化知识,才能收到好的教学效果。通过充分的过程探究,学生得出图像性质,再借助图像直观的性质进而得到一次函数的性质。放手探究,让学生的潜力与智慧充分表现出来,使他们的真实思维和真实自我有机会得到释放和张扬。
教学设计:
第一步 知识回顾
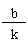 一次函数的一般表达式是y=kx+b(k,b为常数,k≠0)让学生写出一些常数较简单的一次函数表达式。
一次函数的一般表达式是y=kx+b(k,b为常数,k≠0)让学生写出一些常数较简单的一次函数表达式。
画一次函数图像,只需确定两个点(0,b),(- , 0),过这两点作直线。
第二步 动手操作
让学生到前面写出10个一次函数表达式。
让学生说出这些一次函数大致有几种类型。
师写出8个常数简单的一次函数表达式,让学生画出这八个函数的图像(分成8个 小组,6人一组,每组一个),师巡视、指导。
第三步 观察与思考﹣
它们的图像在直角坐标系中位置一样吗?
引导学生从图像变化趋势上观察并分类探索表达式y=kx+b 与图像间的关系。
第四步 一起探究 得出结论
指明探究方向,它们的位置不一样是由什么要素决定的?(分类探究)
由图像性质得出一次函数的性质(直观性语言描述)
从自变量x与函数y之间的变化角度来说明(师引导,生说结论)
教学片段
……
师:一次函数的表达式是y=kx+b(k,b为常数,k≠0),请同学们在黑板上写出一些常数较简单的一次函数表达式行吗?
(学生表现踊跃,写出了10多个)
师:你们认为黑板上这些一次函数大致有几种类型?
生:(讨论一 会儿后)四类,即k﹥0,b>0;k>0,b<0;k<0,b>0;k<0,b<0。
会儿后)四类,即k﹥0,b>0;k>0,b<0;k<0,b>0;k<0,b<0。
(老师在学生板书的函数中不同类型各选了两个,并把常数较复杂的更换成简单的常数,即y=3x+2,y=-2x+3,y=x+1,y=-x+2,y=-2x-2,y=x-2,y=-x-3,y=2x-1)
师:我们来画出这八个函数的图像。
(把任务分配给了8个小组,每组1个,6人一组,在坐标系已画好的黑板上动手操作)
(学生在自己提供的素材上进行再“加工”,兴趣很大,教师到每组巡视、指导。在确认画图全部正确的情况下,老师提出了要求)
师:请同学们组间比较一下,你们的图像在直角坐标系中位置一样吗?
生:(互相 探视后)“不一样”,“有些一样”……
探视后)“不一样”,“有些一样”……
师:有什么不一样?(开始聚焦矛盾)
生:(七嘴八舌)“走向不一样”,“经过的象限不一样”,“我们的图像在原点上方”,“我们的图像在原点下方”……
师:看来有些不一样,那么它们位置的不一样是由什么要素决定的?(教师指明了探究方向,但未指明具体的探究之路是明智的)
生1:是由k、b的取值确定的。
师:很好!我们围绕生1的回答,能得到图像或函数的哪些结论 ?(顺水推舟,放手让学生一搏)
?(顺水推舟,放手让学生一搏)
(热烈讨 论后)
论后)
生2(板书):当k>0时,图像从“左下”到“右上”;当k<0 时,图像从“左上”到“右下”。
生3(板书):当b >0时 ,图像在原点上方;当b <0时,图像在原点下方。
,图像在原点上方;当b <0时,图像在原点下方。
生4(板书):当k>0,b>0 时,图像经过一、二、三象限。
(生5、生6跑到黑板前补充:当事人k>0,b<0时,图像经过一、三、四象限;当k<0,b>0时,图像经过一、二、四象限;当k<0,b<0时,图像经过二、三、四象限)
(这个探究过程约用了10多分钟, 学生体会非常充分,从学生的神情看,绝大多数学生已接受几位同学的板书,但老师未对结论进行优化。这时倒使老师为难了,怎么没有一个学生说出一次函数的性质呢?短暂局促与紧张后,老师确定了思路)
学生体会非常充分,从学生的神情看,绝大多数学生已接受几位同学的板书,但老师未对结论进行优化。这时倒使老师为难了,怎么没有一个学生说出一次函数的性质呢?短暂局促与紧张后,老师确定了思路)
师:刚才你们研究了图像的性质,能否由图像性质得出相应函数的性质呢?
(学生茫然)
师:请看生2的板书,能揣摩图像“走向”的意思吗?
生(七 嘴八舌):当k>0时,图像向上“爬”;当k<0时,图像
嘴八舌):当k>0时,图像向上“爬”;当k<0时,图像 向下“走
”……(未出现老师所预期的结论)
向下“走
”……(未出现老师所预期的结论)
师:好,大家能很贴切地从图像的直观形象来理解图像性质,能不 能从自变量x与函数y之间的变化的角度来说明“向上爬”、“向下走”的含义呢?
能从自变量x与函数y之间的变化的角度来说明“向上爬”、“向下走”的含义呢?
生众:当k>0时,x与y 同向变化,k<0时,x与y异向变化……
师:也就是说,k>0,x增大,y……
生众:增大。
师:k<0时,x……y……
生众:x增大,y减小;x减小,y增大。
(在这里,老师努力避免了知识的“告诉”方式工,而是间接引导)
师:好了,我们就用x与y 之间的变化规律来表达一次函数的性质好吗?请同学们在书上补充图像的性质,并熟悉一下一次函数的性质。
……
教学反思
10. 某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如 下:
下:
|
每人销售件数 |
1800 |
510 |
250 |
210 |
150 |
120 |
|
人 数 |
1 |
1 |
3 |
5 |
3 |
2 |
(1)求这15位营销人员该月销售量的平均数、中位数、众数。
(2)假设销售部负责人把每位营销人员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由。
9. 有14个数据,由小到大排列,其平均数为34,现有一位同学求得这组数据前 8个数的平均数为32,后8个数的平均数为3
8个数的平均数为32,后8个数的平均数为3 6,求这组数据的中位数。
6,求这组数据的中位数。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com