引导学生总结本节的主要知识点，及解题时分析的思路。

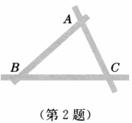
2、分别作AB，BC的垂直平分线，两线相交于点O(如图)，则点O即为所求。可根据线段垂直平分线的性质定理及其逆定理进行证明。

1、8

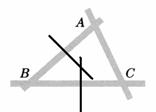
2、已知：如图，三条路围成一个三角地带，要在它的中间建一个市场，并且使市场到三个交叉路口的距离相等。怎样才能找到这个位置呢?画出示意图，并说明理由。

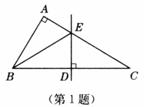
1、已知：如图，在Rt△ABC中，∠A=90°，AB=3，AC=5，BC边的垂直平分线DE交BC于点D，交AC于点E。

求△ABE的周长。

观察下面用尺规作线段垂直平分线的步骤(图24-25)，思考这种作法的依据。

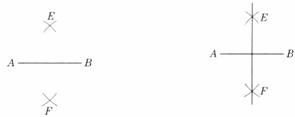
步骤一：分别以点A，B为圆心，以固定长(大于AB长的一半)为半径画弧，两弧分别交于点E，F。

步骤二：过点E，F作直线，则直线EF就是线段AB的垂直平分线。

使学生明白尺规作线段垂直平分线的依据。依据是线段垂直平分线的性质定理的逆定理。

2、垂直的定义，已知，公共边，HL，全等三角形的对应边相等，线段垂直平分线的定义。

由此，我们得到：

线段垂直平分线性质定理的逆定理　 到一条线段两个端点距离相等的点，在这条线段的垂直平分线上。

1、略

2、填写下面命题证明过程的理由。

已知：如图，P为线段AB外的一点，且PA=PB。

求证：点P在线段AB的垂直平分线上。

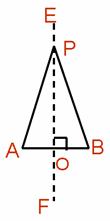
证明：过点P作直线EF⊥AB，垂足为O，则

∠POA＝∠POB＝90°(　　 )。

在Rt△PAO和Rt△PBO中，

PA＝PB(　　 )，

PO＝PO(　　 )，

∴Rt△PAO≌Rt△PBO (　　 )。

∴AO＝BO(　　 )。

∴EF是线段AB的垂直平分线(　　 )。

∴点P在线段AB的垂直平分线上。

加深学生对逆命题和逆定理含义的理解，让学生独立正确地说出线段垂直平分线的性质定理的逆命题和证明过程的依据。

1、写出上面定理的逆命题。