5．为了解我市九年级女生的体能状况，从某校九年级的甲、乙两班中各抽取了27名女生进行了一分钟跳绳测试，测试数据统计结果如下表：

如果每分钟跳绳次数≥105次的为优秀，那么甲、乙两班的优秀率的关系是(　)

A．甲优<乙优　　　　　　 B．甲优>乙优

C．甲优=乙优　　　　　　 D．无法比较

4．有一组数据16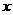，，19，19，它们的平均数比众数小1，则这组数据的平均数和中位数分别是(　)

A．18，17.5　　　　 B．18，19　　　　　 C．19，18　　　　　 D．18，18.5

3．有一组数据，按从小到大的顺序排列为13，14，19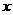，，23，27，28，31，其中位数是22，则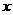等于(　)

A．23　　　 B．22　　　 C．20　　　 D．21

2．在一次数学考试中，第一小组的14名同学的成绩与全班平均分的差是2，3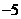，，10，12，8，2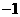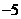，，，4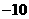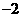，，，5，5(全班平均成绩为83分)，则这个小组的平均成绩是(　)

A．81分　　 B．83分　　 C．85分　　 D．87分

1．为了准备班级里的元旦联欢会，班长以全班同学爱吃哪几种水果作了民意调查，以决定最终买什么水果，最好选用下面哪个数据(　)

A．平均数　　　 B．中位数　　　 C．众数　　 D．以上都不是

　　 本节课通过对确定一次函数表达式方法的探讨过程，引导学生学会对数学对象进行思考，从数和形两方面对一次函数进行深入研究，得出两个条件可确定一个一次函数。在教学中你是否关注了学生的合作探究过程；是否注重了培养学生数形结合的思想方法；是否渗透了应用数学的意识

　　 本节课我们学习了怎样确定一次函数的解析式，在确定一次函数的解析式时可使用待定系数法，即先设出解析式y＝kx+b，再根据题目条件找到满足条件的两对(x，y)的值，(可根据图像、表格或具体问题得出)代人解析式，从而求出k，b的值。

3、已知三点(3，5)，(t，9)，(−4，−9)在同一直线上，则t = ________

例3、已知y−2与x成正比例，当x = 3时，y = 1，求y与x之间的函数关系式

解：设y−2 = kx，(k≠0)，将(3，1)点代入，得

1−2 = 3k，k = −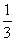

∴y−2 = −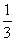x，即y = −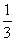x+2

点评：用换元的思想，将y−2看成一个整体。

练一练：已知y是x²的一次函数，当x = −1时，y = 6；当x = 2时，y = 9，试求x，y的函数表达式。

答案：y = x²+5

2、一条直线与x轴的交点为(−3，0)，与y轴的交点为(0，−7)，那么这条直线对应的函数表达式是__________，这条直线与两坐标轴围成的三角形的面积S = ________

　　 想一想：

　　 确定一次函数的表达式需要几个条件？确定正比例函数的表达式呢？

　　 学生讨论：确定一次函数的表达式需要两个条件，确定正比例函数的表达式只需要一个条件。

　　 师：能告诉我你们的理由吗？

　　 引导学生从表达式和函数图像两方面思考。

　　 学生甲：我觉得一次函数的表达式 y=kx+b有两个常数 k， b，要求出　 k和 b的值，因此需要两个条件。而正比例函数中b＝0，只需求k，所以只需一个条件。

　　 学生乙：因为一次函数的图像是一条直线，两点确定一条直线，所以需要两个条件，而正比例函数的图像是经过原点的一条直线，所以只需一点就可以确定这条直线。

师：同学们观察得非常仔细，思考问题比较深入。下面我们结合具体问题来探索如何确定一次函数的表达式。

例1、某物体沿着一个斜坡下滑，它的速度v(米/秒)与其下滑时间t(秒)的关系如图所示．

(1)写出v与t之间的关系；

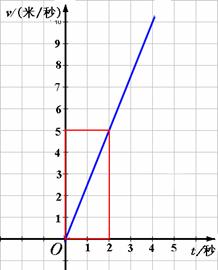(2)下滑3秒时物体的速度是多少？

分析：题目所给信息是函数的图象，首先从图象是一条经过原点的射线判断出该函数应是正比例了函数；其次在函数图象上任取一点(原点除外)，如(2，5)点，代入表达式，就可计算出k值。

解：(1)设v = kt(k≠0)，由图象可得，点(2，5)满足函数关系式，将其代入可得：

5 = 2k，解得k = 2.5

∴v = 2.5t

(2)当t = 3时，v = 2.5×3 = 7.5(米/秒)

在这个例子中，我们先将表达式中的未知系数用字母表示出来，再根据条件求出这个未知系数，这种方法称为待定系数法。

确定正比例函数的表达式需要哪几个条件？确定一次函数的表达式呢？

学生思考，并总结出答案。

例2、写出满足下表的一个一次函数的解析式

解析：设y = kx+b；注意到(0，7)这个特殊点，因此可选取(0，7)，(2，6)代入进行计算，解得：y = −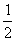x+7

练一练：

1、若一次函数y =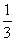x+n的图象经过点A(−3，2)，则n = __________；