
题目列表(包括答案和解析)
7.已知在△ABC中,AB=2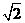 ,AB边上的高为x,△ABC的面积为S.
,AB边上的高为x,△ABC的面积为S.
(1)写出S关于x的函数关系式;
(2)当x=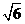 时,△ABC的面积为多少?
时,△ABC的面积为多少?
6.下表反映了两个变量x与y之间的关系,你能发现表中的x与y之间的关系吗?请用解析式表示出来.
|
x |
-21 |
0 |
21 |
42 |
63 |
… |
|
y |
121 |
100 |
79 |
58 |
37 |
… |
5.已知函数y=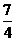 x-2.(1)求x=2时y的值;(2)求y=-1时x的值.
x-2.(1)求x=2时y的值;(2)求y=-1时x的值.
4.下列变量之间的关系:①三角形面积S与它的底边a;②x-y=3中的x与y;③y=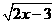 中的y与x;④圆的面积S与圆的半径r,其中成函数关系的有( )
中的y与x;④圆的面积S与圆的半径r,其中成函数关系的有( )
A.2个 B.3个 C.4个 D.1个
3.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
|
支撑物高度h(cm) |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
|
小车下滑时间t(秒) |
4.23 |
3.00 |
2.45 |
2.13 |
1.89 |
1.71 |
1.59 |
1.50 |
下列说法错误的是( )
A.当h=50cm时,t=1.89秒 B.随着h逐渐升高,t逐渐变小
C.h每增加10cm,t减小1.23秒 D.随着h逐渐升高,小车的速度逐渐加快
2.在y=35x+20中,当x=16时,y=_______.
1.半径为r的圆的面积为S,则S与r的函数关系式为______,当r=2时,函数值为_____,它的实际意义是______.
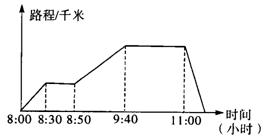
15.小敏骑自行车于上午8:00从A地出发,先到B地游玩一会儿再去C地游玩(如图),已知小敏骑自行车的速度为18千米/时,
(1)小敏在B地和C地共停留了多少时间?(2)从A地到C地的路程是多少?
(3)如果小敏要在中午12时以前赶回A地,她返程的速度至少要多少?
14.李师傅在今年4月1日带了徒弟小王,在师傅的指导下,小王生产的件数每天增加2件,已知师傅每天可生产60件,小王想在第1个月就追上师傅.
(1)求小王的工作效率v(件/天)与工作时间t(天)之间的函数关系式;
(2)求第6天小王的工作效率;
(3)求第几天小王每天可生产38件;
(4)小王的愿望能实现吗?
◆拓展训练
13.已知:功率×做功时间=力×位移.设功率为P,做功时间为t.一辆拖车用了9000牛的力把一辆陷在水沟里的汽车拖出6米,所用时间为t秒.
(1)求P关于t的函数关系式;
(2)如果这辆拖车只用6秒,就把一辆陷在水沟里的汽车拖出6米,问拖车的功率是多少千瓦?
(3)如果改用功率为1.44千瓦的拖车用同样的力把陷在水沟里的汽车拖出6米,则需要多少时间?(1瓦=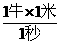 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com