
题目列表(包括答案和解析)
3、选择题:
(1)在一次数学测验中,甲、乙、丙、丁四位同学的分数分别是90、、90、70,若这四个同学得分的众数与平均数恰好相等,则他们得分的中位数是( )
A、100 B、90 C、80 D、70
(2)当5个整数从小到大排列,其中位数是4,如果这组数据的唯一众数是6,则5个整数可能的最大的和是( )
A、21 B、22 C、23 D、24
(3)10名工人,某天生产同一零件,生产达到件数是:15,17,14,10,15,19,17,16,14,12,则这一组数据的众数是( )
A、15 B、17 15 C、14 D、17 15 14
2、根据所给数据,求出平均数、中位数和众数,并填入下表.(精确到0.1)
|
数据 |
平均数 |
中位数 |
众数 |
|
20,20,21,24,27,30,32 |
|
|
|
|
0,2,3,4,5,5,10 |
|
|
|
|
-2,0,3,3,3,8 |
|
|
|
|
―6,―4,―2,2,4,6 |
|
|
|
4.3 中位数和众数 同步练习
基础训练:1、判断题:
(1)给定一组数据,那么描述这组数据的平均数一定只有一个.( )
(2)给定一组数据,那么描述这组数据的中位数一定只有一个.( )
(3)给定一组数据,那么描述这组数据的众数一定只有一个.( )
(4)给定一组数据,那么描述这组数据的平均数一定位于最大值与
最小值之间.( )
(5)给定一组数据,那么描述这组数据的中位数一定位于最大值与
最小值的正中间.( )
(6)给定一组数据,如果找不到众数,那么众数一定就是0.( )
(1)探究新知:如图1,已知△ABC与△ABD的面积相等,
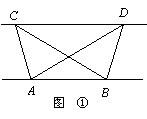 试判断AB与CD的位置关系,并说明理由.
试判断AB与CD的位置关系,并说明理由.
(2)结论应用:
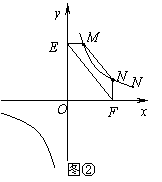 ① 如图2,点M,N在反比例函数
① 如图2,点M,N在反比例函数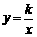 (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
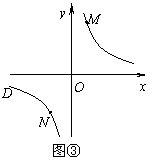 ② 若①中的其他条件不变,只改变点M,N 的位置如图3所示,请判断 MN与EF是否平行.
② 若①中的其他条件不变,只改变点M,N 的位置如图3所示,请判断 MN与EF是否平行.
24、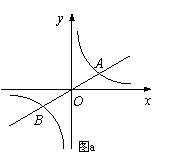 如图a,已知双曲线
如图a,已知双曲线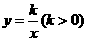 与直线
与直线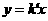 交于A,B
交于A,B
两点,点A在第一象限.试解答下列问题:
(1)若点A的坐标为(4,2),则点B的坐标为 ;若点A
的横坐标为m, 则点B的坐标可表示为 ;
(2)如图b,过原点O作另一条直线l,交双曲线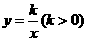 于
于
P,Q两点,点P在第一象限.
①说明四边形APBQ一定是平行四边形;
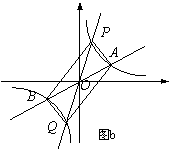 ②设点A,P的横坐标分别为m,n, 四边形APBQ可能是矩形吗? 可能是正方形吗?若可能, 直接写出m,n应满足的条件;若不可能,请说明理由.
②设点A,P的横坐标分别为m,n, 四边形APBQ可能是矩形吗? 可能是正方形吗?若可能, 直接写出m,n应满足的条件;若不可能,请说明理由.
23、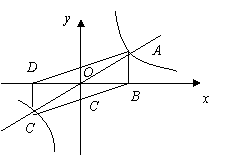 如图,正比例函数y=x与反比例函数y=
如图,正比例函数y=x与反比例函数y=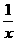 的图象相交于A、C两点,AB⊥x轴于B,CD⊥y轴于D,求四边形ABCD的面积。
的图象相交于A、C两点,AB⊥x轴于B,CD⊥y轴于D,求四边形ABCD的面积。
22、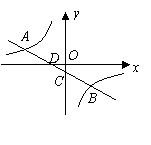 如图,一次函数
如图,一次函数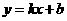 的图象与反比例函数
的图象与反比例函数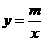 的图象交于
的图象交于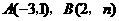 两点,直线
两点,直线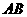 分别交
分别交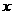 轴、
轴、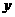 轴于
轴于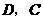 两点.
两点.
(1)求上述反比例函数和一次函数的解析式;(2)求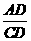 的值.
的值.
21、如图,反比例函数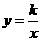 的图象与一次函数
的图象与一次函数 的图象交于
的图象交于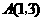 ,
,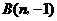 两点。(1)求反比例函数与一次函数的解析式;
两点。(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当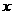 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
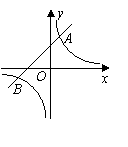
20、如图,已知反比例函数y = 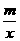 的图象经过点A(1,- 3),一次函数y = kx + b的图象经过点A与点C(0,- 4),且与反比例函数的图象相交于另一点B.
的图象经过点A(1,- 3),一次函数y = kx + b的图象经过点A与点C(0,- 4),且与反比例函数的图象相交于另一点B.
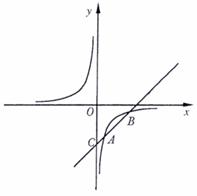 (1)试确定这两个函数的表达式;
(1)试确定这两个函数的表达式;
(2)求点B的坐标.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com