
题目列表(包括答案和解析)
4、用换元法把方程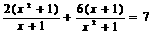 化为
化为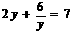 ,那么下列换元方法正确的是 ( ) A、
,那么下列换元方法正确的是 ( ) A、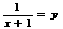 B、
B、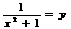 C、
C、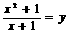 D、
D、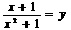
3、长沙市五一商场为了增加销售额,推出“五月销售大酬宾”活动,其活动内容为:“凡五月份在该商场一次性购物超过50元以上者,超过50元的部分按9折优惠”。在大酬宾活动中,李明到该商场为单位购买单价为30元的办公用品x件(x>2),则应付货款y(元)与商品件数x的函数关系式是 ( )
A、y=27x(x>2); B、y=27x+5(x>2); C、y=27x+50(x>2); D、y=27x+45(x>2)
2.已知正比例函数 的图象上两点
的图象上两点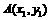 、
、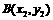 ,当
,当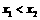 时,有
时,有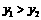 ,那么m的取值范围是( ).
,那么m的取值范围是( ).
(A)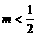 (B)
(B)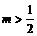 (C)
(C)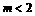 (D)
(D)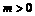
1、函数y=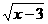 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A、x≥3 B、x>3 C、x<3 D、x≤3
5. (安徽03/21)如图是五角星,已知AC=a,求五角星外接圆的直径(结果用含三角函数的式子表示)。
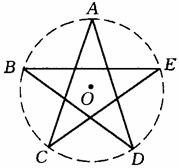
[解]
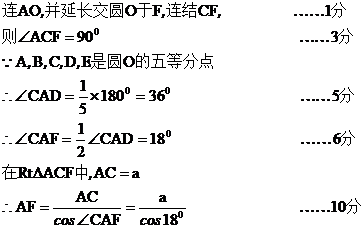
4.
2003资阳市如图,在△ABC中,已知∠ACB=90°,CD⊥AB于D,AC=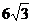 ,BD=3。
,BD=3。
(1)请根据下面求cosA的解答过程,在横线上填上适当的结论,使解答正确完整:
∵CD⊥AB ∠ACB=90°
∴AC= AB cosA, AD =AC·cosA
由已知AC=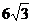 ,BD=3
,BD=3
∴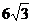 =AB cosA=(AD+BD)cosA=(
=AB cosA=(AD+BD)cosA=(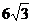 cosA+3)cosA
cosA+3)cosA
设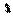 =cosA,则
=cosA,则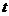 >0,且上式可化为
>0,且上式可化为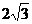
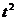 +
+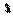 -
-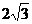 =0,则此解得cosA=
=0,则此解得cosA=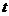 =
=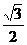
(2)求BC的长及△ABC的面积。
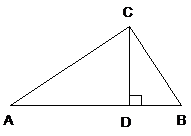
(2)解:在Rt△ABC中,BC=AC·tanA=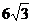 ·
·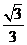 =6
=6
S△ABC=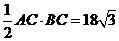
3. (荆门03/19)(本题满分8分)(1)如图1,在△ABC 中,∠B 、∠C
均为锐角,其对边分别为b、c,求证: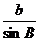 =
=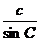 ;
;
(2)在△ABC
中,AB=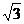 ,AC=
,AC=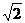 ,∠B
=450,问满足这样的△ABC
有几个?在图2中作出来(不写作法,不述理由)并利用(1)的结论求出∠ACB的大小。
,∠B
=450,问满足这样的△ABC
有几个?在图2中作出来(不写作法,不述理由)并利用(1)的结论求出∠ACB的大小。


2.
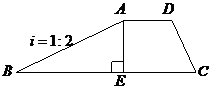 如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比
如图,沿江堤坝的横断面是梯形ABCD,坝顶AD=4m,坝高AE=6 m,斜坡AB的坡比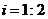 ,∠C=60°,求斜坡AB、CD的长。
,∠C=60°,求斜坡AB、CD的长。
解:∵斜坡AB的坡比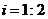 ,
,
∵AE:BE=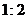 ,又AE=6 m
∴BE=12 m
,又AE=6 m
∴BE=12 m
∴AB=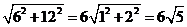 (m)
(m)
作DF⊥BC于F,则得矩形AEFD,有DF=AE=6 m,∵∠C=60° ∴CD=DF·sin60°= m
m
答:斜坡AB、CD的长分别是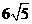 m ,
m ,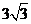 m。
m。
1.
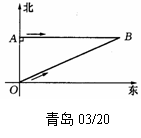 (青岛03/20)(6分)人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只,正以24海里/小时的速度向正东方向航行.为迅速实施检查,巡逻艇调整好航向,以26海里/小时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问⑴需要几小时才能追上?(点B为追上时的位置)⑵确定巡逻艇的追赶方向(精确到0.1°).
参考数据:sin66.8°≈ 0.9191 cos 66.8°≈ 0.393
sin67.4°≈ 0.9231 cos 67.4°≈ 0.3846
sin68.4°≈ 0.9298 cos 68.4°≈ 0.368l
sin70.6°≈ 0.9432 cos70.6°≈ 0.3322
(青岛03/20)(6分)人民海关缉私巡逻艇在东海海域执行巡逻任务时,发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只,正以24海里/小时的速度向正东方向航行.为迅速实施检查,巡逻艇调整好航向,以26海里/小时的速度追赶,在涉嫌船只不改变航向和航速的前提下,问⑴需要几小时才能追上?(点B为追上时的位置)⑵确定巡逻艇的追赶方向(精确到0.1°).
参考数据:sin66.8°≈ 0.9191 cos 66.8°≈ 0.393
sin67.4°≈ 0.9231 cos 67.4°≈ 0.3846
sin68.4°≈ 0.9298 cos 68.4°≈ 0.368l
sin70.6°≈ 0.9432 cos70.6°≈ 0.3322

13、(重庆03/8)已知:如图,梯形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( A ) A、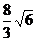 B、
B、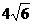 C、
C、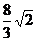 D、
D、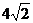


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com