2.理解掌握中心对称的性质,并会进行简单的应用.

1.理解掌握中心对称的意义，发展初步的审美能力，增强对图形欣赏的意识.

2、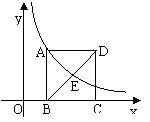已知如图，点A(1，3)在函数y=k/x(x>0)的图像上，矩形ABCD的边BC在x轴上，E为对角线BD的中点，函数y=k/x(x>0)的图像又经过A，E两点，点E的横坐标为m。

(1)求k的值。

(2)求点C的坐标(用m的代数式表示)。

(3)当∠ABD=45°时，求m的值。

1.为了预防春季感冒，某学校对教室采用药熏消毒法进行消毒，已知药物燃烧时，室内每立方米空气中含药量y(mg)与时间x(min)成正比例；药物燃烧后，y与x成反比例(如图)，现测得药物10min燃烧完毕，此时室内空气中每立方米的含药量为8mg，

请根据题中所提供的信息，解答下列问题。

(1)药物燃烧时，y与x的函数关系式为________，自变量x的取值范围为________，药物燃烧后y关于x的函数关系式为___________。

(2)研究表明，当空气中每立方米的含药量低于1.6mg时学生方可进入教室，那么从消毒开始，至少需要经过________min后，学生才能回到教室。

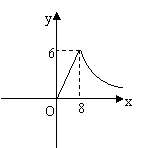(3)研究表明，当空气中每立方米的含药量不低于3mg且持续时间不低于10min时，才能有效杀灭空气中的病菌，那么此次消毒是否有效？为什么？

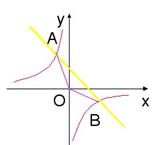
2．如图，已知一次函数y=kx+b(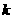≠0)的图象与反比例函数y=-8/x的图象交于A，B两点，且A点的横坐标与B点的纵坐标都是；

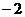(1)　　 一次函数的解析式(5分)。

(2)　　 △AOB的面积(6分)。

1、已知一次函数y=-x+6和反比例函数y=k/x(≠0)

(1)满足什么条件时这两个函数在同一坐标系xoy中图象有两个公共交点(6分)

(2)设(1)中的两个公共点为A，B，则∠AOB是锐角还是钝角(4分)。

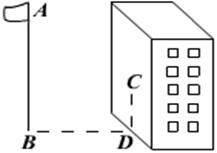
6、如图，某同学想测量旗杆的高度，他在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的应高为2米，求旗杆的高度.

5．已知：反比例函数y=k/x和一次函数y=-2x+1其中一次函数的图像经过点(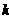，5).

(1)　 试求反比例函数的解析式；

(2)　　　　　　 若点A在第一象限，且同时在上述两函数的图像上，求A点的坐标；

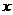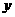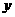4．已知□ABCD中，AB = 4，AD = 2，E是AB边上的一动点，设AE=，DE延长线交CB的延长线于F，设CF =，求与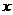之间的函数关系。

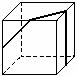
3、(1)一个透明的玻璃正方体内镶嵌了一条铁丝(如图所示的粗线)，请指出右边的两个图是从正方体的哪个方向看到的视图.

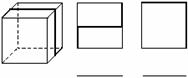(2)如图，粗线表示嵌在玻璃正方体内的一根铁丝，请画出该正方体的主视图、左视图和俯视图.