
题目列表(包括答案和解析)
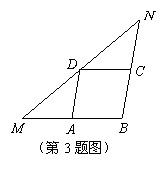
3.在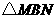 中,
中,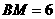 ,点
,点 ,
,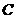 ,
,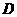 分别在
分别在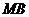 ,
,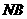 ,
, 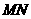 上,四边形
上,四边形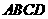 为平行四边形,且
为平行四边形,且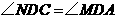 , 则
, 则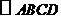 的周长是( )
的周长是( )
A.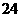 B.
B.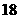 C.
C.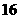 D.
D.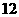
2.若反比例函数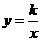 的图象经过点
的图象经过点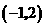 ,则这个函数的图象一定经过点( )
,则这个函数的图象一定经过点( )
 A.
A.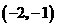 B.
B.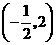 C.
C.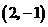 D.
D.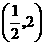
1.气象台预报“本市明天降水概率是80%”,对此信息,下面的几种说法正确的是( )
A.本市明天将有80%的地区降水 B.本市明天将有80%的时间降水
C.明天肯定下雨 D.明天降水的可能性比较大
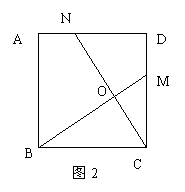
25、问题背景 某课外学习小组在一次学习研讨中,得到了如下两个命题:
①如图1,在正三角形△ABC中,M、N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60º,则BM=CN;
②如图2,在正方形ABCD中,M、N分别是CD、AD上的点,BM与CN相交于点O,若∠BON=90º,则BM=CN;
然后运用类比的思想提出了如下命题:
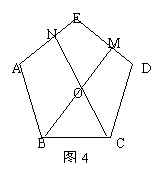
③如图3,在正五边形ABCDE中,M、N分别是CD、DE上的点,BM与CN相交于点O,若∠BON=108º,则BM=CN。
任务要求:
(1)请你从①、②、③三个命题中选择一个进行证明;(说明:选①做对得4分,选②做对得3分,选③做对得5分)
(2)请你继续完成下列探索:
①请在图3中画出一条与CN相等的线段DH,使点H在正五边形的边上,且与CN相交所成的一个角是108º,这样的线段有几条?(不必写出画法,不要求证明)
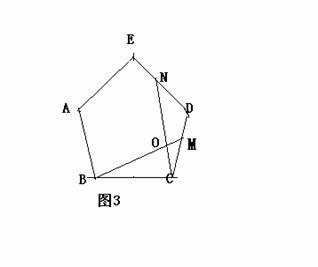
 ②如图4,在正五边形ABCDE中,M、N分别是DE、EA上的点,BM与CN相交于点O,若∠BON=108º,请问结论BM=CN是否还成立?若成立,请给予证明;若不成立,请说明理由。
②如图4,在正五边形ABCDE中,M、N分别是DE、EA上的点,BM与CN相交于点O,若∠BON=108º,请问结论BM=CN是否还成立?若成立,请给予证明;若不成立,请说明理由。

24、一条抛物线y=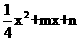 经过点(0,
经过点(0,
(1)求这条抛物线的解析式,并写出它的顶点坐标坐标;
(2)现有一半径为1,圆心P在抛物线上运动的动圆,当⊙P与坐标轴相切时,求轴心P的坐标。
23、小杰到学校食堂买饭,看到A、B两窗口前面排队的人一样多(设为a人,a>8),就站在A窗口队伍的后面,过了2分钟,他发现A窗口每分钟有4人买了饭离开队伍上,B窗口每分钟有6人买了饭离开队伍,且B窗口队伍后面每分钟增加5人。
(1)此时,若小杰继续在A窗口排队,则他到达窗口所花的时间是多少(用含a的代数式表示)?
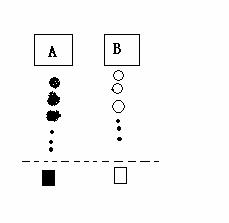 (2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其它因素)。
(2)此时,若小杰迅速从A窗口队伍转移到B窗口后面重新排队,且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少,求a的取值范围(不考虑其它因素)。
22、一次期中考试中,A、B、C、D、E五位同学的数学、英语成绩等有关信息如下表所示:(单位:分)
|
|
A |
B |
C |
D |
E |
平均分 |
标准差 |
|
数学 |
71 |
72 |
69 |
68 |
70 |
|
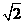 |
|
英语 |
88 |
82 |
94 |
85 |
76 |
85 |
|
(1)求这五位同学在本次考试中数学成绩的平均分和英语成绩的标准差;
(2)为了比较不同学科考试成绩的好与差,采用标准分是一个合理的选择,标准分的计算公式是:标准分=(个人成绩-平均成绩)÷成绩标准差。
从标准分看,标准分大的考试成绩更好。请问A同学在本次考试中,数学与英语哪个学科考得更好?
友情提示:一组数据的标准差计算公式是S=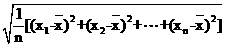 ,其中
,其中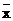 为n个数据
为n个数据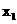 、
、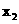 …
…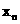 r的平均数。
r的平均数。
21、如图,在梯形ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C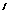 处,折痕DE交BC于点E,连结C
处,折痕DE交BC于点E,连结C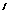 E。
E。
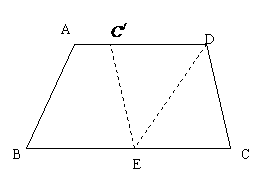 (1)求证:四边形CD C
(1)求证:四边形CD C E是菱形;
E是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明
。
20、如图,AB是⊙0的直径,BC是弦,OD⊥BC于E,交 于D。
于D。
(1)请写出四个不同类型的正确结论;
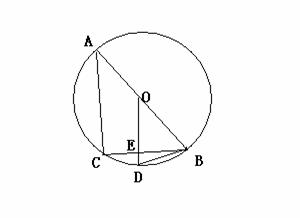 (2)连结CD,设∠CDB=α,∠ABC=β,试找出α与β之间的一种关系式,并予以证明。
(2)连结CD,设∠CDB=α,∠ABC=β,试找出α与β之间的一种关系式,并予以证明。
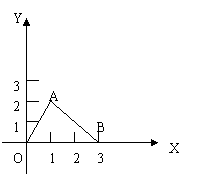
19、如图,在平面直角坐标系中,点A在第一象限,点B的坐标为(3,0),OA=2,∠AOB=60º。(1)求点A的坐标;(2)若直线AB交y轴于点C,求△AOC的面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com