
题目列表(包括答案和解析)
1、C 2、C 3、D 4、A 5、(1)(2)(3)
6、解答:
(1)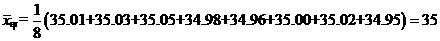 毫米,
毫米,
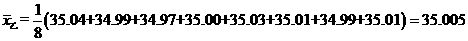 毫米
毫米
(2)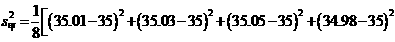
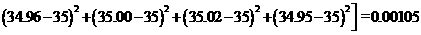 毫米2
毫米2
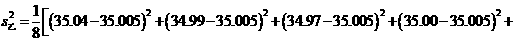
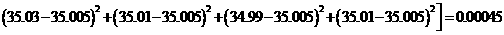
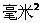
(3)因为,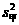 >
>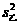 ,所以乙的零件的尺寸更接近于35毫米.
,所以乙的零件的尺寸更接近于35毫米.
[拓展探究]
解答: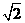
[回顾反思]
解答:如果一组数据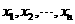 的方差为
的方差为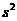 ,则
,则
(1)新数据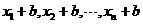 的方差仍为
的方差仍为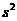
(2)新数据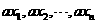 的方差为
的方差为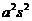
(3)新数据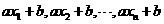 的方差为
的方差为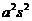
第11课时
 [范例展示]
[范例展示]
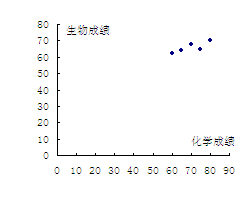
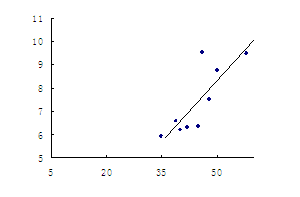
例1、分析:涉及两个变量:化学成绩与生物成绩,可以以化学成绩为自变量,考察因变量生物成绩的变化趋势.
解答:以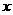 轴表示化学成绩,
轴表示化学成绩, 轴表示生物成绩,可得相应的散点图如图所示:
轴表示生物成绩,可得相应的散点图如图所示:
由散点图可见,两者之间具有相关关系.
反思:判断变量间有无相关关系,一种常用的简便可行的方法就是绘制散点图
例2、分析:画散点图时,横轴和纵轴的长度单位可以不一致.
解答:(1)如图所示
(2)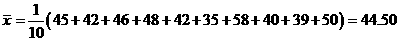
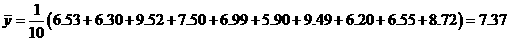
设回归直线的方程为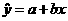 ,则
,则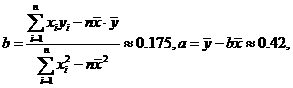
回归直线的方程为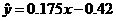 ,回归直线的图形如上图.
,回归直线的图形如上图.
评析:由于横纵轴长度单位不一致,回归直线在图形中的形成和实际情况是不同的.
[自我测评]
1、C 2、C 3、D 4、甲 5、2
6、解答:(1)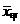 =87,
=87,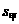 =12.7,
=12.7,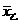 =95,
=95,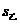 =9.7
=9.7
(2)由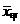 =87<
=87<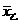 =95,且
=95,且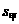 =12.7>
=12.7>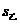 =9.7,故甲的数学学习状况不如乙的数学学习状况.
=9.7,故甲的数学学习状况不如乙的数学学习状况.
[拓展探究]
解答: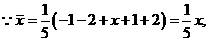
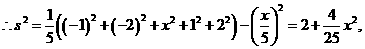
又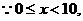 且
且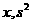 均为整数,
均为整数,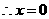 或5.
或5.
当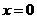 时,
时,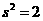 ,所以
,所以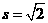 ;当
;当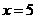 时,
时,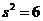 ,所以
,所以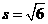 .
.
[回顾反思]
新数据法: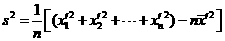 等。
等。
第10课时
[范例展示]
例1、分析:要知道哪种玉米的苗长的高,只要比较甲、乙两种玉米的平均高度即可;要知道哪种玉米的苗长的整齐,只要比较两种玉米苗高的方差大小就可以得到结论.
解答:(1)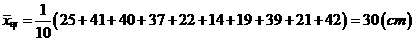 ,
,
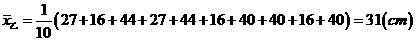 ,
,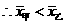 .
.
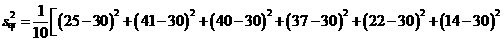 (2)
(2)
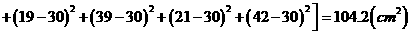
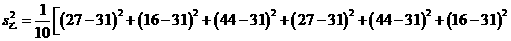
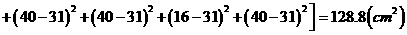
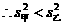 ,所以乙种玉米的苗长的高;甲种玉米的苗长得整齐.
,所以乙种玉米的苗长的高;甲种玉米的苗长得整齐.
评析:比较两组数据平均水平的高低,只需要计算它们的平均数,并比较它们的大小即可,同样,要看两组数据的波动性,只需要计算出它们的方差或标准差,并比较它们的大小即可,但需要注意的是,平均数越大数据平均水平越高;方差或标准差越大,数据的波动越大、稳定性约差.
例2、分析:对照标准差基本公式,先把这两组数据的平均数代数式表示出来,再运用标准差基本公式化简可得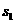 和
和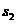 的关系式.
的关系式.
解答:设数据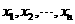 的平均数为
的平均数为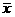 ,即
,即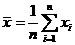 ,设
,设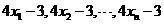 的平均数为
的平均数为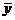 ,即
,即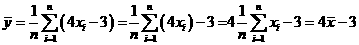 ,
,
所以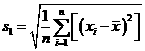 ,
,
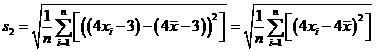
=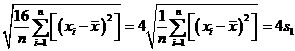 ,所以
,所以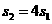 .
.
评析:由本例类似可得如下结论:若把一组数据的每一个数扩大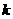 倍并加上一个常数
倍并加上一个常数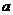 ,则它的标准差扩大
,则它的标准差扩大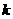 倍,而于常数
倍,而于常数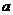 无关.
无关.
[自我测评]
1、A 2、D 3、B 4、2 5、0.065
6、解答: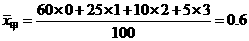 件,
件,
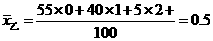 件,由于工人乙平均每天出次品0.5件,低于甲,所以按题意要求应确定乙升任工长.
件,由于工人乙平均每天出次品0.5件,低于甲,所以按题意要求应确定乙升任工长.
[拓展探究]
解答:(1)根据题意,甲两次购粮分别用去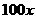 元、
元、 元,乙两次购粮的数量为
元,乙两次购粮的数量为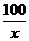 (千克)和
(千克)和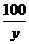 (千克),所以甲两次购粮的平均单价为
(千克),所以甲两次购粮的平均单价为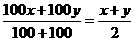 ,乙两次购粮的平均单价为
,乙两次购粮的平均单价为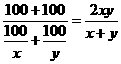 .
.
(2)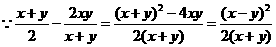 ,又
,又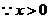 ,
,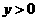 ,
,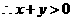 .
.
又由已知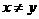 ,
,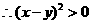 .
.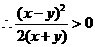 ,
, 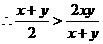 .
.
答:乙两次购粮的平均单价比较低.
[回顾反思]
一组数据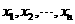 的平均数为
的平均数为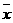 ,则一组新数据
,则一组新数据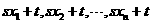 的平均数为
的平均数为
第9课时
[范例展示]
例1、解答:(1)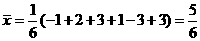 ,
,
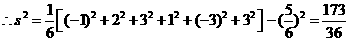 .
.
(2)方法一,用简化公式:
取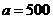 ,则有
,则有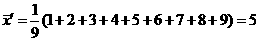 ,
,
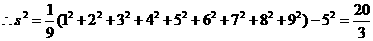 .
.
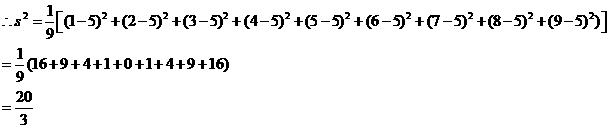 方法二,用新数据法:取
方法二,用新数据法:取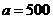 ,则有
,则有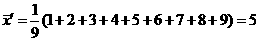 ,
, 例2、解答:取
例2、解答:取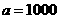 ,取得新数据:
,取得新数据: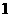 ,
,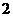 ,
,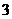 ,
,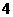 ,5,
,5,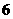 ,
,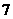 ,
,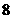 ,
,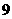 .
.

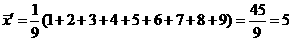 ,
,

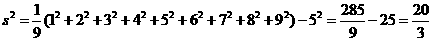 ,
,

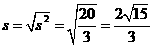 .
.
[自我测评]
1、C 2、B 3、D 4、10 5、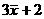
6、解答:班级平均得分
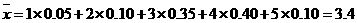 分.
分.
答:该班平均得分3.4分.
[拓展探究]
解答:设甲地到乙地路程为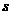 ,则根据题意,得
,则根据题意,得
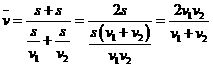 (米/秒)
(米/秒)
[回顾反思]
第8课时
[范例展示]
例1、分析:利用方程的思想,设立未知数,用平均数公式列方程组求解.
解答:设投进3个球的人数为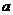 ,投进4个球的人数为
,投进4个球的人数为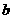 ,则由平均数的意义,可得
,则由平均数的意义,可得
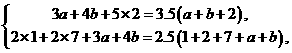 即
即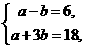 解得
解得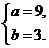
答:投进3个球的人数为9人,投进4个球的人数为3人.
评析:本题实质上考查平均数的概念及计算公式,应用平均数公式得到关系式,转化为方程组问题求解. 例2、分析:首先应计算出样本的平均数,然后用样本的平均数去估计总体的平均数,从而计算出总产量、总收入,进而求出纯收入.
解答:(1)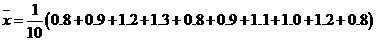 =
=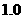 (千克),
(千克),
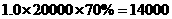 (千克).
(千克).
(2)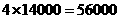 (元),56000
(元),56000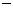 16000=40000(元).
16000=40000(元).
(3)设平均每年的增长率为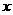 ,根据题意得,
,根据题意得,
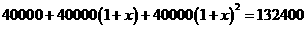 ,解得
,解得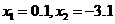 (舍去),
(舍去),
所以增长率为10%.
评析:由于鱼在池塘中,无法精确计算其重量,只有用样本平均数去估计总体平均数,再由成活率,则可以估计池塘中的鱼的总量.
[自我测评]
1、C 2、D 3、A 4、C 5、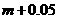
12.要分析学生初中升学的数学成绩对高一年级数学学习有什么影响,在高一年级学生中随机抽选 名学生,分析他们入学的数学成绩(
名学生,分析他们入学的数学成绩(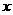 )和高一年级期末数学考试成绩(
)和高一年级期末数学考试成绩( )(如下表):
)(如下表):
|
编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
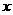 |
63 |
67 |
45 |
88 |
81 |
71 |
52 |
99 |
58 |
76 |
 |
65 |
78 |
52 |
82 |
92 |
89 |
73 |
98 |
56 |
75 |
(1) 画出散点图;
(2)
对变量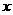 和
和 进行相关性检验,如果
进行相关性检验,如果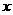 和
和 之间具有线性相关关系,求出一元线性回归方程;
之间具有线性相关关系,求出一元线性回归方程;
(3)
若某学生入学数学成绩为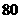 分,试估计他高一年级期末数学考试成绩.
分,试估计他高一年级期末数学考试成绩.
第7课时
[范例展示]
例1、分析:(1)用平均数公式求解;(2)数值较大,可考虑新数据法
解答:(1)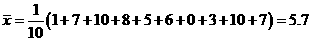
(2)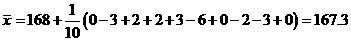
评析:我们在计算平均数时,选择恰当的方法,可以使得计算简单.
例2、分析:(1)将各成绩段人数相加即可;(2)用频数平均数公式计算平均成绩.
解答:(1)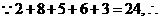 共有24名运动员参加比赛.
共有24名运动员参加比赛.
(2)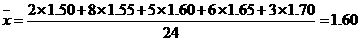 (米).
(米).
所以这些运动员的平均成绩为1.60米.
评析:本题也可以用新数据法计算其平均成绩.在用平均数公式解决实际问题时,要灵活选择恰当的平均数计算方法,这样才能使计算简便.
[自我测评]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com