
题目列表(包括答案和解析)
5. 右图的矩形,长为2米,宽为1米. 在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗, 据此可以估计出图中阴影部分的面积为
右图的矩形,长为2米,宽为1米. 在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗, 据此可以估计出图中阴影部分的面积为
A.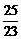 平方米
B.
平方米
B.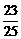 平方米
C.
平方米
C.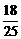 平方米 D.
平方米 D.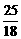 平方米
平方米
4.某公司共有工作人员200人,其中职员160人,中级管理人员30人,高级管理人员10人.现要从中抽取20个人进行身体健康检查,如果采用分层抽样的方法,则职员、中级管理人员和高级管理人员各应抽取的人数分别为
A. 16,3,1 B.16,2,2 C.8,15,7 D.12,3,5
3.已知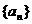 为等差数列,且
为等差数列,且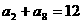 ,则
,则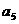 等于
等于
A.7 B.6 C.5 D.4
2.若一个几何体的主视图和侧视图都是等腰梯形,则这个几何体可能是
A.圆柱 B.棱锥 C. 球体 D.圆台
1.在程序框图中,表示判断框的图形符号是



 A.
A.
 B.
C.
D.
B.
C.
D.
20、解:函数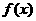 为奇函数,
为奇函数,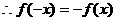
所以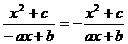 ,
,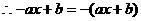 ,即
,即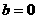
任意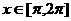 ,
,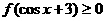 恒成立,
恒成立,
当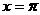 时,
时,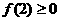 …… 4分
…… 4分
(2)任意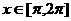 ,
,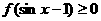 恒成立
恒成立
当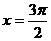 时,
时,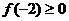 ,又
,又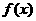 为奇函数,
为奇函数,

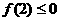 所以
所以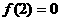
代入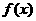 , 得到
, 得到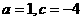 ,所以
,所以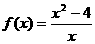 …… 9分
…… 9分
(3)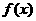 在
在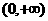 上单调递增且为奇函数
上单调递增且为奇函数
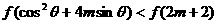 ,又
,又 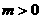 ,
,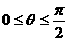 ,
,

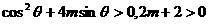 ,
,

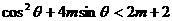 ,即
,即 
即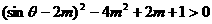
令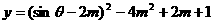 ,令
,令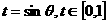 ,
,

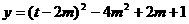 ,
,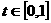
① 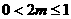 ,即
,即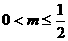 ,则
,则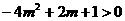 ,
,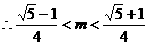 ,所以
,所以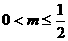
② 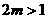 ,即
,即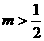 ,则
,则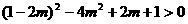
即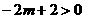 ,
,
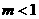 ,所以
,所以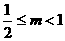
21.在 中,内角
中,内角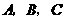 对边的边长分别是
对边的边长分别是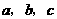 ,已知
,已知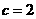 ,
,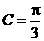 .
.
(Ⅰ)若 的面积等于
的面积等于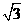 ,求
,求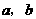 ;
;
(Ⅱ)若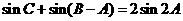 ,求
,求 的面积.
的面积.
解:(Ⅰ)由余弦定理及已知条件得,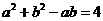 ,
,
又因为 的面积等于
的面积等于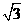 ,所以
,所以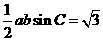 ,得
,得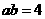 .
.
联立方程组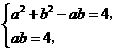 解得
解得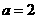 ,
,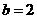 .
.
(Ⅱ)由题意得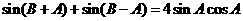 ,
,
即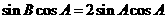 ,
,
当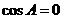 时,
时,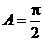 ,
,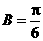 ,
,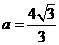 ,
,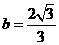 ,
,
当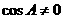 时,得
时,得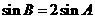 ,由正弦定理得
,由正弦定理得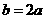 ,
,
联立方程组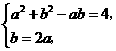 解得
解得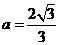 ,
,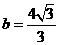 .
.
所以 的面积
的面积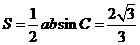 .
. 

22已知函数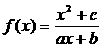 为奇函数,
为奇函数,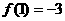 ,且对任意
,且对任意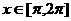 ,
,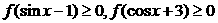 恒成立。
恒成立。
 (1)求
(1)求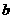 及证明
及证明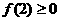 ;
;
(2)求证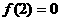 并求
并求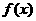 解析式;
解析式;
(3)若当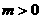 ,
, 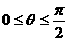 时,恒有
时,恒有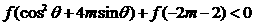 ,求
,求 的取值范围.
的取值范围.
20.已知函数 的一部分图象如下图所示,
的一部分图象如下图所示,
如果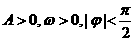
(1)求函数的解析式

 (2)将函数f(x)的图像按向量
(2)将函数f(x)的图像按向量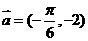 平移后得到函数g(x),
平移后得到函数g(x),
求g(x)得单调减区间和对称中心。
解:(1)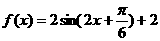
(2)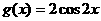
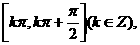
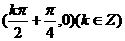
19.已知向量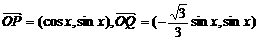 ,定义函数
,定义函数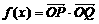 .
.
(I)求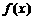 的最小正周期和最大值及相应的x值;
的最小正周期和最大值及相应的x值;
(II)当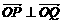 时,求x的值.
时,求x的值.
(1)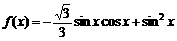
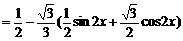 …………(2分)
…………(2分)
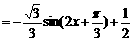 ……………………(4分)
……………………(4分)
∴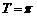 ,当
,当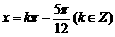 时:
时:
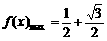 ………………………………(8分)
………………………………(8分)
(2)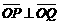 ,即
,即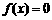 ,即
,即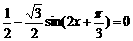 ……(10分)
……(10分)
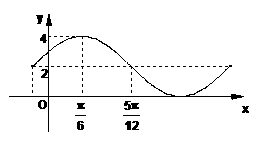 解得:
解得: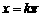 或
或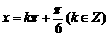 ……………………(12分)
……………………(12分)
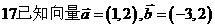
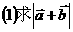


.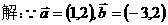
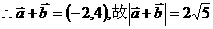
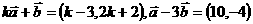
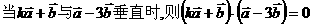
18.已知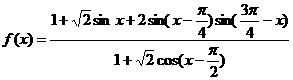
(1)化简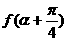 ;(2)若
;(2)若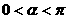 ,且
,且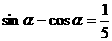 ,求
,求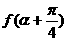 的值.
的值.
(1)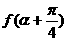 =
=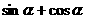 (2)
(2)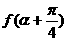 =
=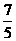
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com