
题目列表(包括答案和解析)
20.(本题13分)设数列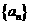 的前
的前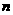 项和为
项和为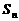 ,若对任意
,若对任意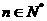 ,都有
,都有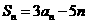 .
.
(1)求数列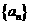 的首项;
的首项;
(2)求证:数列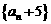 是等比数列,并求数列
是等比数列,并求数列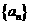 的通项公式;
的通项公式;
(3)数列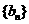 满足
满足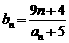 ,问是否存在
,问是否存在 ,使得
,使得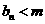 恒成立?如果存在,求出
恒成立?如果存在,求出 的值,如果不存在,说明理由.
的值,如果不存在,说明理由.
2009-2010学年度第二学期期中考试
高一年级期中试卷答卷纸(2010.4.)
19.(本题9分)数列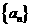 的前n项和
的前n项和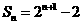 ,
,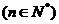 .
.
(1)求数列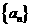 的通项公式;
的通项公式;
(2)若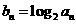 ,
,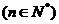 ,设数列
,设数列 的前
的前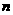 项和为
项和为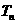 ,求数列{
,求数列{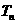 }中的最小项.
}中的最小项.
18.(本题8分)某村计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3 宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
宽的空地,当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?
17.(本题10分)设数列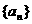 是等差数列,数列
是等差数列,数列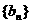 是各项都为正数的等比数列,且
是各项都为正数的等比数列,且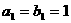 ,
,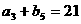 ,
,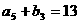 .
.
(1)求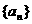 、
、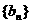 的通项公式;(2)求数列
的通项公式;(2)求数列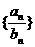 的前10项和
的前10项和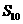 .
.
16.(本题9分)在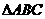 中,
中,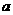 、
、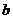 、
、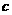 分别是角A、B、C的对边,且
分别是角A、B、C的对边,且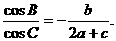
(1)求角B的大小;
(2)若 ,求
,求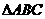 的面积.
的面积.
15.(本题9分)已知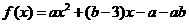 ,当
,当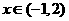 时,
时,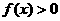 ;
;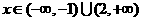 时,
时,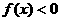
(1)求a、b的值;
(2)若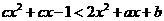 的解集为R,求 c的取值范围。
的解集为R,求 c的取值范围。
14.若不等式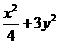 ≥
≥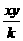 ,对任意的正实数
,对任意的正实数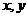 总成立,则正实数
总成立,则正实数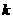 的取值范围为: ▲ .
的取值范围为: ▲ .
13.在等差数列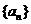 中,若公差为
中,若公差为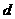 ,前n项和为
,前n项和为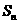 ,,则数列
,,则数列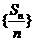 为等差数列,公差为
为等差数列,公差为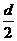 ,类似地,在等比数列
,类似地,在等比数列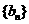 中,若公比为
中,若公比为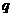 ,前n项积为
,前n项积为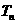 ,则数列
,则数列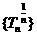 为等比数列,公比为 ▲ .
为等比数列,公比为 ▲ .
12.已知数列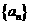 满足
满足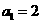 ,
,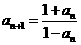 ,
,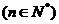 ,则
,则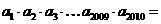 ▲ .
▲ .
11.已知函数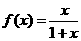 ,仿照等差数列求和公式的推导方法化简:
,仿照等差数列求和公式的推导方法化简: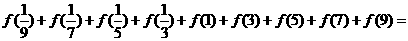 ▲ .
▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com