
题目列表(包括答案和解析)
11. 求值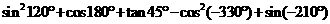 = .
= .
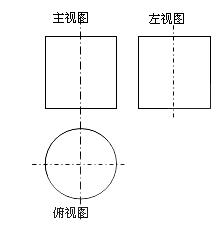
10.如图,一个空间几何体的主视图和左视图都是边长为1的正方形,
俯视图是一个圆,那么这个几何体的侧面积为 .
9. 某校有学生2000人,其中高二学生630人,高三学生720人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高一学生的人数为 .
某校有学生2000人,其中高二学生630人,高三学生720人.为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本.则样本中高一学生的人数为 .
22.(文理)解:(1)由点P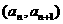 在直线
在直线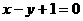 上,即
上,即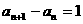 ,且
,且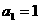 ,数列{
,数列{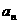 }是以1为首项,1为公差的等差数列
}是以1为首项,1为公差的等差数列
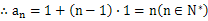 (文4分,理3分)
(文4分,理3分)
(2)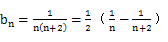
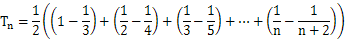 (文8分)
(文8分)
=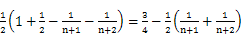 (文12分 理6分)
(文12分 理6分)
(3)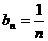 ,可得
,可得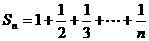 ,
,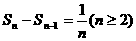
即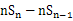 =1
=1 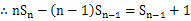
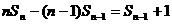 ,
,
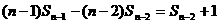
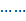
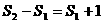
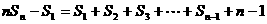
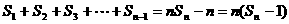 ,n≥2
,n≥2
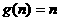 故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.(理12分)
故存在关于n的整式g(x)=n,使得对于一切不小于2的自然数n恒成立.(理12分)
w.w.^w.k.&s.5*
 w.w.^w.k.&s.5*
w.w.^w.k.&s.5*
高考在线
高☆考♂资♀源?
21.(文理)解:设生产甲产品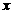 吨,生产乙产品
吨,生产乙产品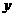 吨,
吨,
则有: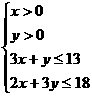 (2分)
(2分)
目标函数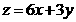 (4分)
(4分)
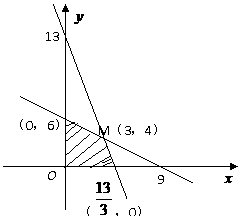
如图作出可行域(6分)
由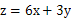 知
知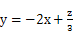
作出直线系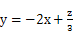 ,当直线经过可行域上的点M时,纵截距达到最大,(8分)
,当直线经过可行域上的点M时,纵截距达到最大,(8分)
即z达到最大。
由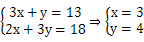 (10分)
(10分) 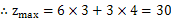
答:甲产品生产3吨.乙产品生产4吨时,企业获得最大利润,最大利润为30万元.(12分)w.w.^w.k.&s.5*
18.(文理) S=60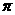 +4
+4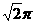 ;(6分) V=52
;(6分) V=52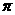 -
-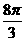 =
=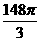 .(12分)
.(12分)
(文)19. 解:(1)在⊿ABC中,由余弦定理得: ∠
∠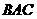 =
=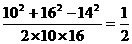
∴∠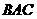 =60°(6分)
=60°(6分)
(2)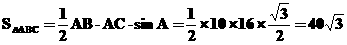 (12分)
(12分)
(理)19. (1)在⊿ABC中,由余弦定理得: ∠
∠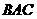 =
=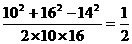
∴∠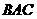 =60° (3分)
=60° (3分)
设⊿ABC的外接圆半径为R,由正弦定理得:
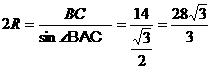 ∴R=
∴R=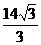 .
. (6分w.w.^w.k.&s.5*)
(6分w.w.^w.k.&s.5*)
(2)由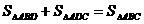 , ( 9分)
, ( 9分)
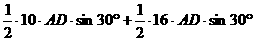
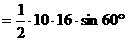
 求得
求得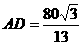 (12分)w.w.^w.k.&s.5*
(12分)w.w.^w.k.&s.5*
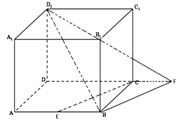
(文理)20解:如图,在平面ABCD内,过B作BF//CE,交直线CD于F,(4分)
则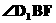 (或补角)为异面直线EC与
(或补角)为异面直线EC与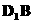 所成的角。(6分)
所成的角。(6分)
在Δ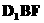 中,易得
中,易得 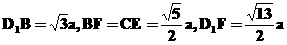 ,(9分)
,(9分)
 由余弦定理得:
由余弦定理得: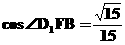 。故异面直线D1B与EC所成的角为
。故异面直线D1B与EC所成的角为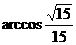 。(12分)
。(12分)
22.(本小题满分12分)
已知数列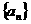 中,
中,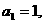 且点P(
且点P(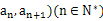 在直线
在直线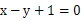 上.
上.
(1)求数列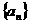 的通项公式;
的通项公式;
(2)设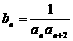 ,求数列
,求数列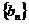 的前
的前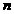 项和
项和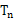 ;
;
期中答案 w.w.^w.k.&s.5*高一数学
文A卷:DBBCC BADBD 文B卷:ABBDC BCDAD
理A卷:CBBAD BCDBD 理B卷:BBBCC BDDAD
文11. 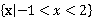 12.
12.  13.
4 14.
13.
4 14. 15.食指 16.
15.食指 16.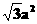
理11. 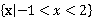 12.
12.  13.
8 14.
13.
8 14. 15.食指 16.(1)(2)(4)
15.食指 16.(1)(2)(4)
(文理)17.
解: (1)由题意: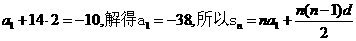 =
=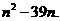 (5分)
(5分)
(2)由题意: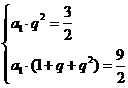 解得
解得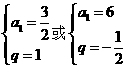 (10分)
(10分)
21.(本小题满分12分)某企业生产甲.乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润6万元,每吨乙产品可获得利润3万元。该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.求甲乙两种产品各生产多少吨时,该企业可获得最大利润,并求出最大利润?
w.w.^w.k.&s.5*
20.(满分12分)在棱长为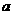 的正方体ABCD-A1B1C1D1, E为AB的中点, 求异面直线EC与
的正方体ABCD-A1B1C1D1, E为AB的中点, 求异面直线EC与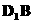 所成的角.
所成的角.
19.在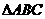 中,
中, 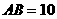 ,
,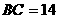 ,
,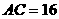 ,
,
(1)求角A的大小
(2)求该三角形的面积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com