
题目列表(包括答案和解析)
2.函数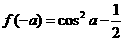 的最小正周期( )
的最小正周期( )
A.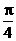 B.
B.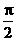 C.
C.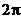 D.
D.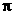
D
1.若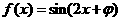 是偶函数,则
是偶函数,则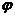 的一个值可为( )
的一个值可为( )
A.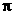 B.
B.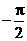 C.
C.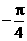 D.
D.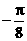
B
12、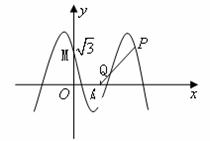 如图所示,函数
如图所示,函数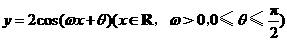 的图象与
的图象与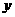 轴相交于点M
轴相交于点M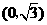 ,且该函数的最小正周期为
,且该函数的最小正周期为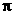 .
.
(1)
求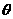 和
和 的值; (2)已知点
的值; (2)已知点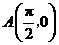 ,点
,点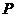 是该函数图象上一点,点
是该函数图象上一点,点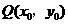 是
是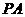 的中点,当
的中点,当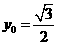 ,
,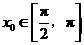 时,求
时,求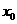 的值
的值
11.如图,某公园摩天轮的半径为40m,点O距地面的高度为50m,摩天轮做匀速转动,每3min转一圈,摩天轮上的点P的起始位置在最低点处.
(Ⅰ)已知在时刻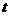 (min)时点P距离地面的高度
(min)时点P距离地面的高度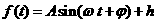 ,求2006min时点P距离地面的高度;
,求2006min时点P距离地面的高度;
 (Ⅱ)当离地面50+20
(Ⅱ)当离地面50+20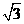 m以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园全貌?
m以上时,可以看到公园的全貌,求转一圈中有多少时间可以看到公园全貌?
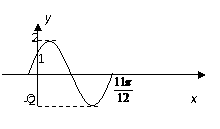
10.已知函数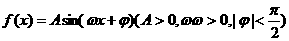 在一个周期内的图象 下图所示。
在一个周期内的图象 下图所示。
(1)求函数的解析式;
 (2)设
(2)设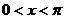 ,且方程
,且方程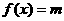 有两个不同的实数根,求实数m的取值范围和这两个根的和。
有两个不同的实数根,求实数m的取值范围和这两个根的和。
9.(本小题13分)已知函数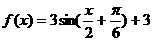
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出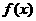 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)说明此函数图象可由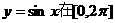 上的图象经怎样的变换得到.
上的图象经怎样的变换得到.
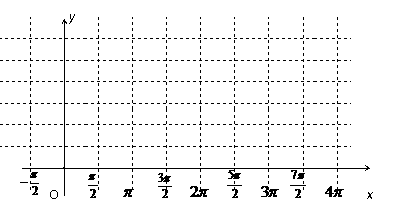
8、函数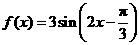 的图象为
的图象为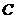 ,则如下结论中正确的序号是 _____
,则如下结论中正确的序号是 _____
①、图象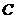 关于直线
关于直线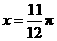 对称; ②、图象
对称; ②、图象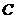 关于点
关于点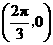 对称;
对称;
③、函数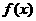 在区间
在区间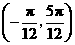 内是增函数;
内是增函数;
④、由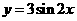 的图角向右平移
的图角向右平移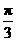 个单位长度可以得到图象
个单位长度可以得到图象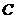 .
.
7.已知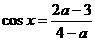 ,且x是第二、三象限角,则a的取值范围是________
,且x是第二、三象限角,则a的取值范围是________
6. 已知函数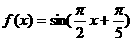 ,若对任意
,若对任意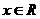 都有
都有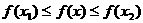 成立,则
成立,则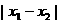 的最小值是____________.
的最小值是____________.
5、设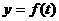 是某港口水的深度
是某港口水的深度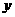 (米)关于时间t(时)的函数,其中
(米)关于时间t(时)的函数,其中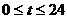 .下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:
|
X |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
Y |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数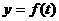 的图象可以近似地看成函数
的图象可以近似地看成函数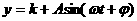 的图象.下面的函数中,最能近似表示表中数据间对应关系的函数有(填序号)________
的图象.下面的函数中,最能近似表示表中数据间对应关系的函数有(填序号)________
(1).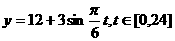 (2).
(2).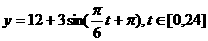
(3).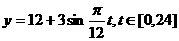 (4).
(4).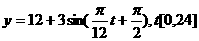
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com